《理論》〈電気回路〉[H24:問2]RLC正弦波交流回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，$ \ RLC \ $正弦波交流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。

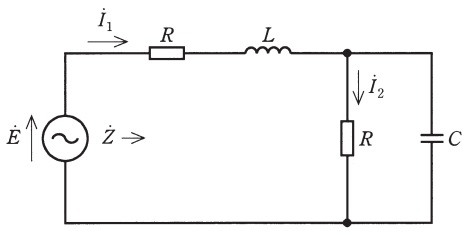
図に示す$ \ RLC \ $回路を考える。正弦波交流電圧$ \ \dot E \ $の角周波数は$ \ \omega \left( \omega ＞0 \right) \ $とする。いま，電源電圧$ \ \dot E \ $と電流$ \ {\dot I}_{1} \ $が同相であるとする。このとき，電圧源$ \ \dot E \ $からみた回路のインピーダンスを$ \ \dot Z \ $とおくと，$ \ \dot Z \ $は純抵抗となり，$ \ \dot Z=\fbox {　（１）　} \ $となる。また，インダクタンス$ \ L \ $は$ \ L=\fbox {　（２）　} \ $となる。

電流の分流比に着目すると，$ \ {\dot I}_{1} \ $と$ \ {\dot I}_{2} \ $について，$ \ \displaystyle \left| \frac {{\dot I}_{2}}{{\dot I}_{1}}\right| ^{2} =\fbox {　（３）　} \ $となる。$ \ {\dot I}_{1} \ $が流れる抵抗$ \ R \ $の消費電力を$ \ P_{1} \ $，$ \ {\dot I}_{2} \ $が流れる抵抗$ \ R \ $の消費電力を$ \ P_{2} \ $とする。電圧源が$ \ RLC \ $回路に供給する電力を$ \ P \ $とおくと，$ \ P=P_{1}+P_{2} \ $となり，$ \ \displaystyle \frac {P_{2}}{P} =\fbox {　（４）　} \ $となる。

この回路では，電源電圧$ \ \dot E \ $と電流$ \ {\dot I}_{1} \ $が同相であることから$ \ R \ $と$ \ \displaystyle \sqrt {\frac {L}{C}} \ $の大小関係は常に$ \ \fbox {　（５）　} \ $となる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　R\frac {1}{1+\omega ^{2}C^{2}R^{2}}　　　&（ロ）&　\frac {CR^{2}}{2+\omega ^{2}C^{2}R^{2}}　　　&（ハ）&　\sqrt {\frac {L}{C}}＞R \\[ 5pt ] &（ニ）&　\frac {1}{1+\omega ^{2}C^{2}R^{2}}　　　&（ホ）&　\sqrt {\frac {L}{C}}=R　　　&（ヘ）&　R\frac {\omega ^{2}C^{2}R^{2}}{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] &（ト）&　\frac {2+\omega ^{2}C^{2}R^{2}}{1+\omega ^{2}C^{2}R^{2}}　　　&（チ）&　\frac {\omega ^{2}C^{2}R^{2}}{1+\omega ^{2}C^{2}R^{2}}　　　　&（リ）&　R\frac {2+\omega ^{2}C^{2}R^{2}}{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] &（ヌ）&　\frac {CR}{1+\omega ^{2}C^{2}R^{2}}　　　&（ル）&　\frac {1}{2+\omega ^{2}C^{2}R^{2}}　　　&（ヲ）&　\sqrt {\frac {L}{C}}＜R \\[ 5pt ] &（ワ）&　\frac {\omega CR}{1+\omega ^{2}C^{2}R^{2}}　　　&（カ）&　\frac {\omega ^{2}C^{2}R^{2}}{2+\omega ^{2}C^{2}R^{2}}　　　&（ヨ）&　\frac {CR^{2}}{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

交流回路のインピーダンスや消費電力に関する計算問題です。３種の頃から似たような問題を解いてきたと思います。２種なので少し計算が複雑になり(5)はやや難易度が高めですが，確実に理解するようにしましょう。

1.合成インピーダンス
インピーダンス$ \ {\dot Z}_{1} \ $と$ \ {\dot Z}_{2} \ $が与えられている時，それぞれの合成インピーダンス$ \ {\dot Z} \ $は以下の式で与えられます。

①直列
直列合成インピーダンス$ \ {\dot Z} \ $は，
\[
\begin{eqnarray}
{\dot Z}&=&{\dot Z}_{1}+{\dot Z}_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成インピーダンス$ \ {\dot Z} \ $は，
\[
\begin{eqnarray}
\frac {1}{{\dot Z}}&=&\frac {1}{{\dot Z}_{1}}+\frac {1}{{\dot Z}_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
{\dot Z}&=&\frac {{\dot Z}_{1}{\dot Z}_{2}}{{\dot Z}_{1}+{\dot Z}_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：リ
$ \ R \ $と$ \ C \ $の合成インピーダンス$ \ {\dot Z}_{1} \ $は，ワンポイント解説「1.合成インピーダンス」の通り，
\[
\begin{eqnarray}
{\dot Z}_{1}&=&\frac {R\cdot \displaystyle \frac {1}{\mathrm {j}\omega C}}{R+ \displaystyle \frac {1}{\mathrm {j}\omega C}} \\[ 5pt ] &=&\frac {R}{1+\mathrm {j}\omega CR} \\[ 5pt ] \end{eqnarray}
\] となり，回路全体の合成インピーダンス$ \ \dot Z \ $は，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L+{\dot Z}_{1} \\[ 5pt ] &=&R+\mathrm {j}\omega L+\frac {R}{1+\mathrm {j}\omega CR} \\[ 5pt ] &=&R+\mathrm {j}\omega L+\frac {R\left( 1-\mathrm {j}\omega CR\right) }{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] &=&R+\frac {R }{1+\omega ^{2}C^{2}R^{2}}+\mathrm {j}\left( \omega L-\frac {\omega CR^{2} }{1+\omega ^{2}C^{2}R^{2}}\right) \\[ 5pt ] \end{eqnarray}
\] となる。ここで，$ \ \dot Z \ $は純抵抗であるから，虚数項は零となるので，
\[
\begin{eqnarray}
\dot Z&=&R+\frac {R }{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] &=&R\left( 1+\frac {1}{1+\omega ^{2}C^{2}R^{2}}\right) \\[ 5pt ] &=&R\left( \frac {1+\omega ^{2}C^{2}R^{2}}{1+\omega ^{2}C^{2}R^{2}}+\frac {1}{1+\omega ^{2}C^{2}R^{2}}\right) \\[ 5pt ] &=&R\frac {2+\omega ^{2}C^{2}R^{2}}{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヨ
$ \ \dot Z \ $は純抵抗であるから，虚数項は零となるので，
\[
\begin{eqnarray}
\omega L-\frac {\omega CR^{2} }{1+\omega ^{2}C^{2}R^{2}}&=&0 \\[ 5pt ] \omega L&=&\frac {\omega CR^{2} }{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] L&=&\frac {CR^{2} }{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ニ
分流の法則より，
\[
\begin{eqnarray}
{\dot I}_{2}&=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C}}{R+ \displaystyle \frac {1}{\mathrm {j}\omega C}}{\dot I}_{1} \\[ 5pt ] &=&\frac {1}{1+\mathrm {j}\omega CR}{\dot I}_{1} \\[ 5pt ] \frac {{\dot I}_{2}}{{\dot I}_{1}}&=&\frac {1}{1+\mathrm {j}\omega CR} \\[ 5pt ] \end{eqnarray}
\] となるので，その絶対値は，
\[
\begin{eqnarray}
\left| \frac {{\dot I}_{2}}{{\dot I}_{1}}\right| &=&\frac {1}{\sqrt{1^{2}+\left( \omega CR\right) ^{2}}} \\[ 5pt ] &=&\frac {1}{\sqrt {1+\omega ^{2}C^{2}R^{2}}} \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
\left| \frac {{\dot I}_{2}}{{\dot I}_{1}}\right| ^{2}&=&\frac {1}{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
(3)より，
\[
\begin{eqnarray}
\left| {\dot I}_{2}\right| ^{2}&=&\frac {1}{1+\omega ^{2}C^{2}R^{2}}\left| {\dot I}_{1}\right| ^{2} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
\frac {P_{2}}{P}&=&\frac {P_{2}}{P_{1}+P_{2}} \\[ 5pt ] &=&\frac {R\left| {\dot I}_{2}\right| ^{2}}{R\left| {\dot I}_{1}\right| ^{2}+R\left| {\dot I}_{2}\right| ^{2}} \\[ 5pt ] &=&\frac {\left| {\dot I}_{2}\right| ^{2}}{\left| {\dot I}_{1}\right| ^{2}+\left| {\dot I}_{2}\right| ^{2}} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{1+\omega ^{2}C^{2}R^{2}}\left| {\dot I}_{1}\right| ^{2} }{\left| {\dot I}_{1}\right| ^{2}+\displaystyle \frac {1}{1+\omega ^{2}C^{2}R^{2}}\left| {\dot I}_{1}\right| ^{2}} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{1+\omega ^{2}C^{2}R^{2}} }{1+\displaystyle \frac {1}{1+\omega ^{2}C^{2}R^{2}}} \\[ 5pt ] &=&\frac {1}{1+\omega ^{2}C^{2}R^{2}+1} \\[ 5pt ] &=&\frac {1}{2+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
(2)解答式より，
\[
\begin{eqnarray}
L&=&\frac {CR^{2} }{1+\omega ^{2}C^{2}R^{2}} \\[ 5pt ] L+\omega ^{2}C^{2}R^{2}L&=&CR^{2} \\[ 5pt ] \omega ^{2}C^{2}R^{2}L&=&CR^{2}-L \\[ 5pt ] \end{eqnarray}
\] となり，左辺は全て正の値なので，右辺も正となる。したがって，
\[
\begin{eqnarray}
CR^{2}-L&＞&0 \\[ 5pt ] CR^{2}&＞&L \\[ 5pt ] R^{2}&＞&\frac {L}{C} \\[ 5pt ] R&＞&\displaystyle \sqrt {\frac {L}{C}} \\[ 5pt ] \end{eqnarray}
\] と求められる。