《理論》〈電気回路〉[H24:問6]抵抗数を増加させた直流回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，直流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。

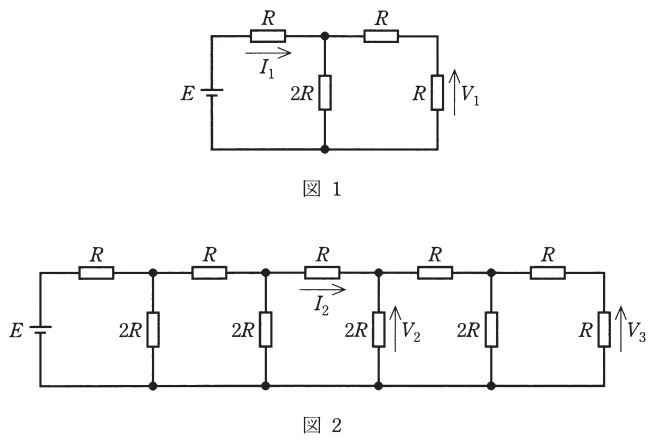
図のように抵抗$ \ R \ $，$ \ 2R \ $，電圧源$ \ E \ $を接続した回路がある。図の電流$ \ I_{1} \ $，$ \ I_{2} \ $と電圧$ \ V_{1} \ $，$ \ V_{2} \ $，$ \ V_{3} \ $を求めたい。

図1の回路において電流$ \ I_{1} \ $は$ \ \fbox {　（１）　} \ $であり，電圧$ \ V_{1} \ $は$ \ \fbox {　（２）　} \ $である。各抵抗に流れる電流の関係を考えると，図2のように抵抗の数が増えても電流や電圧は容易に求めることができる。図2の電流$ \ I_{2} \ $は$ \ \fbox {　（３）　} \ $であり，電圧$ \ V_{2} \ $は$ \ \fbox {　（４）　} \ $，電圧$ \ V_{3} \ $は$ \ \fbox {　（５）　} \ $である。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {E}{6}　　　　　　　&（ロ）&　\frac {2E}{5}　　　　　　　&（ハ）&　\frac {E}{4} \\[ 5pt ] &（ニ）&　\frac {E}{32}　　　&（ホ）&　\frac {E}{16}　　　&（ヘ）&　\frac {E}{R} \\[ 5pt ] &（ト）&　\frac {E}{8R}　　　&（チ）&　\frac {E}{2}　　　　&（リ）&　\frac {E}{3R} \\[ 5pt ] &（ヌ）&　\frac {E}{4R}　　　&（ル）&　\frac {E}{2R}　　　&（ヲ）&　\frac {E}{3} \\[ 5pt ] &（ワ）&　\frac {E}{8}　　　&（カ）&　\frac {E}{64} 　　　&（ヨ）&　\frac {E}{5R} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

キルヒホッフの法則とこの回路における電圧電流の法則性が見つかれば，比較的短時間で解ける問題と言えると思います。２種ではこういう問題を確実に得点できるかどうかが合否の分かれ目となると考えて下さい。

【解答】

(1)解答：ル
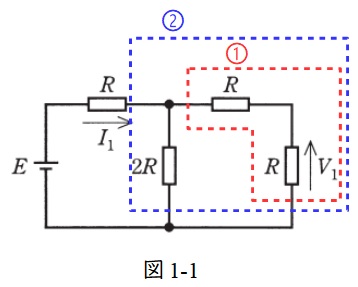
図1-1に示す①の合成抵抗は直列合成抵抗であるから，
\[
\begin{eqnarray}
R+R&=&2R \\[ 5pt ] \end{eqnarray}
\] となり，②の合成抵抗は並列合成抵抗であるから，
\[
\begin{eqnarray}
\frac {2R\cdot 2R}{2R+2R}&=&R \\[ 5pt ] \end{eqnarray}
\] となる。よって，回路全体の合成抵抗は，
\[
\begin{eqnarray}
R+R&=&2R \\[ 5pt ] \end{eqnarray}
\] となるので，電流$ \ I_{1} \ $は，
\[
\begin{eqnarray}
I_{1}&=&\frac {E}{2R} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ハ
①の合成抵抗が$ \ 2R \ $であるから，分流の法則より，$ \ V_{1} \ $の抵抗を流れる電流$ \ I_{\mathrm {V1}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {V1}}&=&\frac {2R}{2R+2R}I_{1} \\[ 5pt ] &=&\frac {1}{2}\cdot \frac {E}{2R} \\[ 5pt ] &=&\frac {E}{4R} \\[ 5pt ] \end{eqnarray}
\] となるので，電圧$ \ V_{1} \ $は，
\[
\begin{eqnarray}
V_{1}&=&RI_{\mathrm {V1}} \\[ 5pt ] &=&R\cdot \frac {E}{4R} \\[ 5pt ] &=&\frac {E}{4} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ト
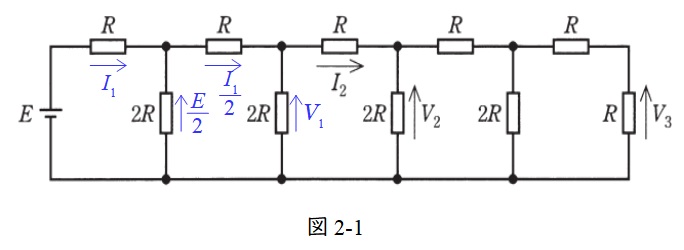
(1)，(2)より，図2-1の通り，本問の回路は段数を重ねていく毎に電圧も電流も$ \ \displaystyle \frac {1}{2} \ $倍していくことが分かるので，
\[
\begin{eqnarray}
I_{2}&=&\frac {1}{2}\cdot \frac {I_{1}}{2} \\[ 5pt ] &=&\frac {1}{2}\cdot \frac {\displaystyle \frac {E}{2R}}{2} \\[ 5pt ] &=&\frac {E}{8R} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ワ
電圧も同様に段数を重ねていく毎に$ \ \displaystyle \frac {1}{2} \ $倍していくので，
\[
\begin{eqnarray}
V_{2}&=&\frac {1}{2}V_{1} \\[ 5pt ] &=&\frac {1}{2}\cdot \frac {E}{4} \\[ 5pt ] &=&\frac {E}{8} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
$ \ V_{3} \ $も同様に，
\[
\begin{eqnarray}
V_{3}&=&\frac {1}{2}\times \frac {1}{2}\cdot V_{2} \\[ 5pt ] &=&\frac {1}{4}\cdot \frac {E}{8} \\[ 5pt ] &=&\frac {E}{32} \\[ 5pt ] \end{eqnarray}
\] と求められる。