《理論》〈電子理論〉[H25:問6]電子のサイクロトロン共鳴に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，電子のサイクロトロン共鳴に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

速度$ \ v \ $，質量$ \ m \ $，単位電荷$ \ q \ $を持つ電子を進行方向と垂直の磁場$ \ B \ $のなかに入れると，フレミングの左手の法則に従って，電荷の進む方向と磁場の両者に対して直角のローレンツ力を受け，その大きさは$ \ qvB \ $である。この力により，電子は等速円運動を始めるが，等速円運動の向心力は，円運動の半径を$ \ r \ $とすれば$ \ \fbox {　（１）　} \ $となる。これが$ \ qvB \ $と等しいことから，半径は$ \ \fbox {　（２）　} \ $となる。

さて静止している電子を速度$ \ v \ $まで加速するのに必要な電圧を$ \ V \ $とする。この$ \ V \ $を用いると速度$ \ v \ $は$ \ \fbox {　（３）　} \ $となる。そこで電子をある半径$ \ r \ $で等速円運動をさせるときに必要な電子のエネルギーに相当する電圧は$ \ \fbox {　（４）　} \ $となる。

一方，この等速円運動は応用においてはその各周波数(サイクロトロン角周波数：単位時間当たりの回転角度)が重要であるが，これは$ \ \fbox {　（５）　} \ $となる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {2\pi qB}{m}　　　　　&（ロ）&　\sqrt {\frac {qV}{2m}}　　　　　&（ハ）&　\frac {qBr}{m} \\[ 5pt ] &（ニ）&　\frac {mv}{r}　　　&（ホ）&　mrv^{2}　　　&（ヘ）&　\sqrt {\frac {qB^{2}}{2mV}} \\[ 5pt ] &（ト）&　\sqrt {\frac {2qV}{m}}　　　&（チ）&　\frac {qB^{2}r^{2}}{2m}　　　&（リ）&　\sqrt {\frac {V}{2qm}}　 \\[ 5pt ] &（ヌ）&　\frac {v}{qmB}　　　&（ル）&　qrB　　　&（ヲ）&　\frac {mv}{qB} \\[ 5pt ] &（ワ）&　\frac {mv^{2}}{r}　　　&（カ）&　\frac {qB}{mv} 　　　&（ヨ）&　\frac {qB}{m} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電子の磁場中での運動は問題がほぼパターン化されています。基本公式をきちんと理解して完答できるようにしましょう。

1.フレミングの左手の法則
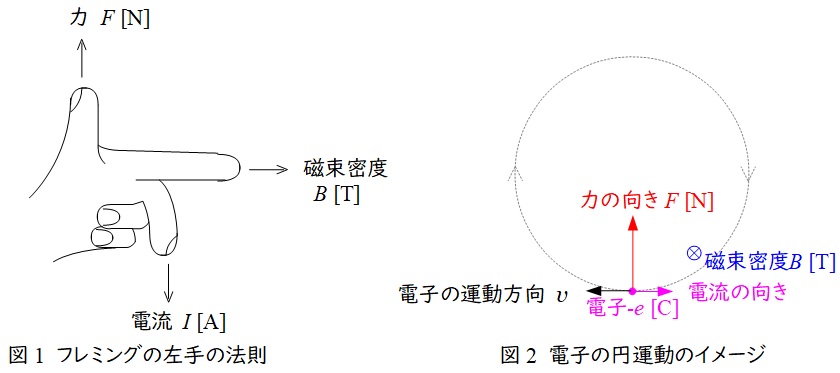
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
この理論は磁場中の電子の運動理論にも応用でき，電子の進む方向と逆方向が電流の向きとすると，図2のように中心に向かう力がかかり，電子の円運動が発生するようになります。
その中心に向かう力の大きさ$ \ F \ $は，電子の電荷を$ \ -e \ $，電子の速度を$ \ v \ $，磁束密度の大きさを$ \ B \ $とすると，
\[
\begin{eqnarray}
F &=&evB \ \mathrm {[N]} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ワ
等速円運動において，中心に向かう向心力の大きさ$ \ F \ $は，
\[
\begin{eqnarray}
F &=&\frac {mv^{2}}{r} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヲ
ローレンツ力と向心力の大きさが等しいことから，
\[
\begin{eqnarray}
qvB &=&\frac {mv^{2}}{r} \\[ 5pt ] r &=&\frac {mv}{qB} 　　　・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ト
静止している電子を速度$ \ v \ $まで加速するのに必要な電圧を$ \ V \ $とした時，そのエネルギーの大きさ$ \ E \ $は，
\[
\begin{eqnarray}
E &=&\frac {1}{2}mv^{2} \\[ 5pt ] E &=&qV \\[ 5pt ] \end{eqnarray}
\] とそれぞれ表すことができるため，この$ \ 2 \ $式から，
\[
\begin{eqnarray}
\frac {1}{2}mv^{2} &=&qV \\[ 5pt ] v^{2} &=&\frac {2qV}{m} \\[ 5pt ] v &=&\sqrt {\frac {2qV}{m}} 　・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：チ
②を$ \ V \ $について整理すると，
\[
\begin{eqnarray}
V &=&\frac {mv^{2}}{2q} 　　　　 \ ・・・・・・・・・・　③ \\[ 5pt ] \end{eqnarray}
\] となる。①を$ \ v \ $について整理すると，
\[
\begin{eqnarray}
v &=&\frac {qBr}{m} 　　　　　・・・・・・・・・・　④ \\[ 5pt ] \end{eqnarray}
\] となるので，これを③に代入すると，
\[
\begin{eqnarray}
V &=&\frac {m}{2q} \left( \frac {qBr}{m}\right) ^{2} \\[ 5pt ] &=&\frac {qB^{2}r^{2}}{2m} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヨ
角周波数を$ \ \omega \ $とすると，$ \ v=r\omega \ $の関係があるため，この関係式と④より，
\[
\begin{eqnarray}
\omega &=&\frac {v}{r} \\[ 5pt ] &=&\frac {\displaystyle \frac {qBr}{m}}{r} \\[ 5pt ] &=&\frac {qB}{m} \\[ 5pt ] \end{eqnarray}
\] と求められる。