《理論》〈電子理論〉[R05:問6]真空中における交流電界中の電子の運動に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，真空中における交流電界中の電子の運動に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

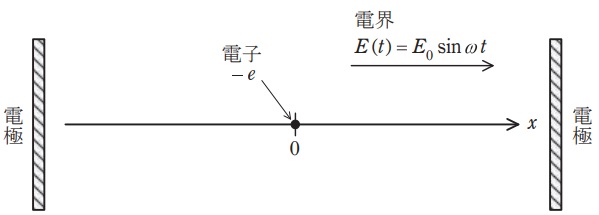
図のように\( \ x \ \)軸を定め，原点から十分離れた平行平板電極が作る一様な交流電界\( \ E \left( t\right) \ \)を，振幅\( \ E_{0}\left( ＞0 \right) \ \)，角周波数\( \ \omega \ \)として，\( \ E \left( t\right) =E_{0}\sin \omega t \ \)とする。時刻\( \ t=0 \ \)で原点\( \ \left( x=0 \right) \ \)に電子が一つ存在する状況を考える。なお，電子の質量を\( \ m \ \)，電荷量を\( \ -e \left( e＞0 \right) \ \)とし，電子の速度は\( \ x \ \)軸に沿った方向のみを考えるものとし，質量の変化が無視できる範囲とする。電子は電界から力\( \ F \ \)を受けて運動する。\( \ F \ \)の正の方向を\( \ x \ \)軸の正の方向にとると，\( \ F= \ \fbox {　 （１） 　} \ \times \sin \omega t \ \)と表される。電子の速度を\( \ v \ \)とし，\( \ v \ \)の正の方向を\( \ x \ \)軸の正の方向にとると，運動の第\( \ 2 \ \)法則より，次の微分方程式が得られる。
\[
\begin{eqnarray}
\frac {\mathrm {d}v}{\mathrm {d}t} &=& \ \fbox {　 （２） 　} \ \times \sin \omega t \\[ 5pt ] \end{eqnarray}
\] \( \ t=0 \ \)における電子の速度を\( \ v_{0}\left( ＞0 \right) \ \)とすると，時刻\( \ t\left( ＞0 \right) \ \)における電子の速度\( \ v\left( t \right) \ \)は，上の微分方程式を\( \ t \ \)で積分することにより，
\[
\begin{eqnarray}
v\left( t \right) &=&v_{0}- \ \fbox {　 （３） 　} \ \left( 1-\cos \omega t \right) \\[ 5pt ] \end{eqnarray}
\] と表される。さらに，時刻\( \ t \ \)における電子の位置\( \ x\left( t \right) \ \)は，\( \ x\left( t \right) = \ \fbox {　 （４） 　} \ \)となる。このことから，電子が原点を中心に同じ区間を往復運動し続けるためには，角周波数が\( \ \omega = \ \fbox {　 （５） 　} \ \)でなければならないことがわかる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　-emE_{0}　　　　　&（ロ）&　-\frac {eE_{0}}{m} \\[ 5pt ] &（ハ）&　-\frac {E_{0}}{em} 　　　　　&（ニ）&　\frac {eE_{0}}{mv_{0}} \\[ 5pt ] &（ホ）&　\frac {mE_{0}}{e\omega } 　　　　　&（ヘ）&　-eE_{0} \\[ 5pt ] &（ト）&　v_{0}t+\frac {eE_{0}}{m\omega ^{2}}\sin \omega t　　　　　&（チ）&　\left( v_{0}-\frac {eE_{0}}{m\omega ^{2}}\right) t+\frac {eE_{0}}{m\omega }\sin \omega t \\[ 5pt ] &（リ）&　\frac {mE_{0}}{ev_{0}}　　　　　&（ヌ）&　-mE_{0} \\[ 5pt ] &（ル）&　-\frac {m}{eE_{0}}　　　　　&（ヲ）&　\frac {eE_{0}\omega }{m} \\[ 5pt ] &（ワ）&　\frac {eE_{0}}{m\omega }　　　　　&（カ）&　\left( v_{0}-\frac {eE_{0}}{m\omega }\right) t+\frac {eE_{0}}{m\omega ^{2}}\sin \omega t \\[ 5pt ] &（ヨ）&　\frac {ev_{0}}{mE_{0}} && \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

交流電界中の電子の運動に関する問題です。
微分方程式を解いていくため，過渡現象の微分方程式の解き方がうろ覚えの受験生だとかなり厳しい問題であったかと思います。
微分方程式の変数分離の中身を理解して解けるようになりましょう。

1.電荷に働く力の大きさ
一様な電界\( \ E \ \mathrm {[V / m]} \ \)が電荷\( \ q \ \mathrm {[C]} \ \)にかかっているとき，この電荷\( \ q \ \mathrm {[C]} \ \)に働く力の大きさ\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] となります。

2.運動方程式（力学）
質量\( \ m \ \mathrm {[kg]} \ \)の物体に力\( \ F \ \mathrm {[N]} \ \)がかかっている時，この物体にかかる加速度\( \ a \ \mathrm {[m / s^{2}]} \ \)との間には，
\[
\begin{eqnarray}
F &=&ma \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)解答：ヘ
交流電界\( \ E \left( t\right) =E_{0}\sin \omega t \ \)があるとき，電荷量\( \ -e \ \)の電子に加わる力\( \ F \ \)の大きさは，ワンポイント解説「1.電荷に働く力の大きさ」の通り，
\[
\begin{eqnarray}
F &=&-eE \left( t\right) \\[ 5pt ] &=&-eE_{0}\sin \omega t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ロ
運動の第\( \ 2 \ \)法則より，電子の加速度\( \ \displaystyle a=\frac {\mathrm {d}v}{\mathrm {d}t} \ \)の大きさは，ワンポイント解説「2.運動方程式（力学）」の通り，
\[
\begin{eqnarray}
a &=&\frac {F}{m} \\[ 5pt ] \frac {\mathrm {d}v}{\mathrm {d}t} &=&-\frac {eE_{0}}{m}\sin \omega t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
（２）解答式の微分方程式を変数分離すると，
\[
\begin{eqnarray}
\mathrm {d}v &=&-\frac {eE_{0}}{m}\sin \omega t \mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となるので，これを積分すると，
\[
\begin{eqnarray}
v \left( t\right) &=&\int -\frac {eE_{0}}{m}\sin \omega t \mathrm {d}t \\[ 5pt ] &=&-\frac {eE_{0}}{m}\int \sin \omega t \mathrm {d}t \\[ 5pt ] &=&-\frac {eE_{0}}{m}\left( -\frac {1}{\omega }\cos \omega t \right) +C 　\left( C \ は積分定数\right) \\[ 5pt ] &=&\frac {eE_{0}}{m\omega }\cos \omega t+C \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\( \ t=0 \ \)における電子の速度は\( \ v_{0} \ \)であるから，
\[
\begin{eqnarray}
v_{0}&=&\frac {eE_{0}}{m\omega }\cos \left( \omega \times 0 \right) +C \\[ 5pt ] &=&\frac {eE_{0}}{m\omega } +C \\[ 5pt ] C&=&v_{0}-\frac {eE_{0}}{m\omega } \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
v \left( t\right) &=&\frac {eE_{0}}{m\omega }\cos \omega t+v_{0}-\frac {eE_{0}}{m\omega } \\[ 5pt ] &=&v_{0}-\frac {eE_{0}}{m\omega }\left( 1-\cos \omega t \right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：カ
\( \ \displaystyle v \left( t\right) =\frac {\mathrm {d}x\left( t\right) }{\mathrm {d}t} \ \)であるから，（３）解答式は，
\[
\begin{eqnarray}
\frac {\mathrm {d}x\left( t\right) }{\mathrm {d}t}&=&v_{0}-\frac {eE_{0}}{m\omega }\left( 1-\cos \omega t \right) \\[ 5pt ] \mathrm {d}x\left( t\right) &=&\left\{ v_{0}-\frac {eE_{0}}{m\omega }\left( 1-\cos \omega t \right) \right\} \mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となるので，これを積分すると，
\[
\begin{eqnarray}
x\left( t\right) &=&\int \left\{ v_{0}-\frac {eE_{0}}{m\omega }\left( 1-\cos \omega t \right) \right\} \mathrm {d}t \\[ 5pt ] &=&\int \left( v_{0}-\frac {eE_{0}}{m\omega }+\frac {eE_{0}}{m\omega }\cos \omega t \right) \mathrm {d}t \\[ 5pt ] &=&\left( v_{0}-\frac {eE_{0}}{m\omega }\right) t+\frac {eE_{0}}{m\omega ^{2}}\sin \omega t +C^{\prime } 　\left( C^{\prime } \ は積分定数\right) \\[ 5pt ] \end{eqnarray}
\] となる。ここで\( \ t=0 \ \)における電子の位置\( \ x=0 \ \)であるから，
\[
\begin{eqnarray}
0 &=&\left( v_{0}-\frac {eE_{0}}{m\omega }\right) \times 0+\frac {eE_{0}}{m\omega ^{2}}\sin \left( \omega \times 0\right) +C^{\prime } \\[ 5pt ] C^{\prime } &=&0 \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
x\left( t\right) &=&\left( v_{0}-\frac {eE_{0}}{m\omega }\right) t+\frac {eE_{0}}{m\omega ^{2}}\sin \omega t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
電子が原点を中心に同じ区間を往復運動し続けるためには，（４）解答式の第１項が零にならなければならないので，
\[
\begin{eqnarray}
v_{0}-\frac {eE_{0}}{m\omega } &=&0 \\[ 5pt ] v_{0} &=&\frac {eE_{0}}{m\omega } \\[ 5pt ] \omega &=&\frac {eE_{0}}{mv_{0}} \\[ 5pt ] \end{eqnarray}
\] でなければならない。