《理論》〈電子理論〉[H25:問7]トランジスタ増幅回路の設計に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

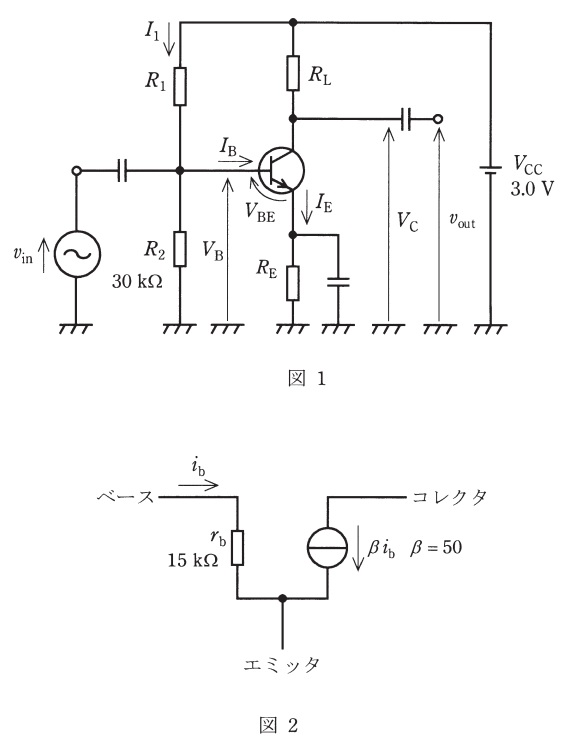
次の文章は，トランジスタ増幅回路の設計に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。ただし，図1のトランジスタ増幅回路において，$ \ v_{\mathrm {in}} \ $は小信号正弦波入力電圧，$ \ v_{\mathrm {out}} \ $は小信号正弦波出力電圧である。

いま，抵抗$ \ R_{\mathrm {1}} \ $を流れる電流$ \ I_{\mathrm {1}} \ $と比較して直流ベース電流$ \ I_{\mathrm {B}} \ $を無視できると仮定する。まず，直流ベース電圧$ \ V_{\mathrm {B}} \ $を$ \ 1.2 \ \mathrm {[V]} \ $とするためには，電流$ \ I_{\mathrm {1}} \ $が$ \ \fbox {　（１）　} \ \mathrm {[\mu A]} \ $となるので，抵抗$ \ R_{\mathrm {1}} \ $を$ \ \fbox {　（２）　} \ \mathrm {[k\Omega ]} \ $と求めることができる。次に，トランジスタのベース・エミッタ間の直流電圧$ \ V_{\mathrm {BE}} \ $を$ \ 0.70 \ \mathrm {[V]} \ $と仮定する。直流エミッタ電流$ \ I_{\mathrm {E}} \ $を$ \ 0.10 \ \mathrm {[mA]} \ $とするために，抵抗$ \ R_{\mathrm {E}} \ $を$ \ \fbox {　（３）　} \ \mathrm {[k\Omega ]} \ $とする。さらに，直流コレクタ電圧$ \ V_{\mathrm {C}} \ $を$ \ 2.1 \ \mathrm {[V]} \ $に設定するために，抵抗$ \ R_{\mathrm {L}} \ $を$ \ \fbox {　（４）　} \ \mathrm {[k\Omega ]} \ $とする。

最後に，これまでに求めた素子値を用いて，図1のトランジスタ増幅回路の電圧増幅度$ \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ $を求めることにする。トランジスタの交流等価回路が図2で表され，また，すべてのコンデンサを正弦波交流信号の周波数において短絡とみなすと，図1のトランジスタ増幅回路の電圧増幅度$ \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ $の絶対値は$ \ \fbox {　（５）　} \ $となる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　0.50　　　　　&（ロ）&　0.90　　　　　&（ハ）&　3.0 \\[ 5pt ] &（ニ）&　4.0　　　　　&（ホ）&　5.0　　　　　&（ヘ）&　9.0 \\[ 5pt ] &（ト）&　15　　　　　&（チ）&　20　　　　　&（リ）&　30 \\[ 5pt ] &（ヌ）&　40　　　　　&（ル）&　45　　　　　&（ヲ）&　50 \\[ 5pt ] &（ワ）&　60　　　　　&（カ）&　90　　　　　&（ヨ）&　300 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

典型的な電子回路の電圧増幅度を導出する問題です。一般的には小信号等価回路は回路図が与えられていることが多いですが，本問では小信号等価回路を覚えている必要があります。それほど難しい等価回路ではないので，確実に記憶しておくようにしましょう。

【解答】

(1)解答：ヌ
問題図において，直流ベース電流$ \ I_{\mathrm {B}} \ $を無視できるので，$ \ R_{\mathrm {1}} \ $を流れる電流$ \ I_{\mathrm {1}} \ $はそのまま$ \ R_{\mathrm {2}} \ $に流れる。直流ベース電圧$ \ V_{\mathrm {B}} \ $を$ \ 1.2 \ \mathrm {[V]} \ $，$ \ R_{\mathrm {2}} \ $を$ \ 30 \ \mathrm {[k\Omega ]} \ $とするので，
\[
\begin{eqnarray}
I_{1} &=&\frac {V_{\mathrm {B}}}{R_{\mathrm {2}}} \\[ 5pt ] &=&\frac {1.2}{30\times 10^{3}} \\[ 5pt ] &=&4.0\times 10^{-5} \ \mathrm {[A]}　→　40 \ \mathrm {[\mu A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ル
オームの法則より，
\[
\begin{eqnarray}
R_{1} &=&\frac {V_{\mathrm {CC}}-V_{\mathrm {B}}}{I_{1}} \\[ 5pt ] &=&\frac {3.0-1.2}{4.0\times 10^{-5}} \\[ 5pt ] &=&4.5\times 10^{4} \ \mathrm {[\Omega ]}　→　45 \ \mathrm {[k \Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ホ
ベース電圧$ \ V_{\mathrm {B}} \ $が$ \ 1.2 \ \mathrm {[V]} \ $，ベース・エミッタ間の直流電圧$ \ V_{\mathrm {BE}} \ $が$ \ 0.70 \ \mathrm {[V]} \ $であるため，エミッタ電圧$ \ V_{\mathrm {E}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm {E}} &=&V_{\mathrm {B}}-V_{\mathrm {BE}} \\[ 5pt ] &=&1.2-0.7 \\[ 5pt ] &=&0.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となり，エミッタ電流$ \ I_{\mathrm {E}} \ $が$ \ 0.10 \ \mathrm {[mA]} \ $であるため，抵抗$ \ R_{\mathrm {E}} \ $は，
\[
\begin{eqnarray}
R_{\mathrm {E}} &=&\frac {V_{\mathrm {E}}}{I_{\mathrm {E}}} \\[ 5pt ] &=&\frac {0.5}{0.10\times 10^{-3}} \\[ 5pt ] &=&5.0\times 10^{3} \ \mathrm {[\Omega ]}　→　5.0 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヘ
ベース電流を無視できるので，コレクタ電流$ \ I_{\mathrm {C}} \ $とエミッタ電流$ \ I_{\mathrm {E}} \ $の大きさはほぼ等しいと考えられる。したがって，$ \ R_{\mathrm {L}} \ $の大きさは，
\[
\begin{eqnarray}
R_{\mathrm {L}} &=&\frac {V_{\mathrm {CC}}-V_{\mathrm {C}}}{I_{\mathrm {C}}} \\[ 5pt ] &=&\frac {3.0-2.1}{0.10\times 10^{-3}} \\[ 5pt ] &=&9.0\times 10^{3} \ \mathrm {[\Omega ]}　→　9.0 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：リ
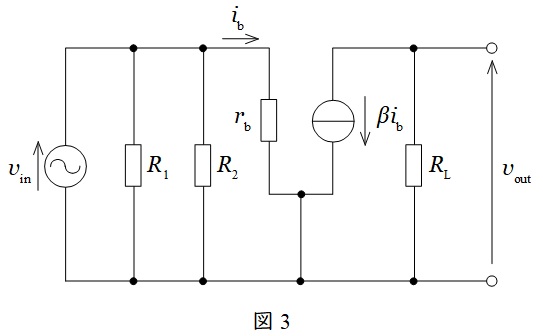
図1の小信号等価回路は図3のように描ける。図3より，
\[
\begin{eqnarray}
v_{\mathrm {in}} &=&r_{\mathrm {b}}i_{\mathrm {b}} \\[ 5pt ] v_{\mathrm {out}} &=&R_{\mathrm {L}}\beta i_{\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
\left| \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}\right| &=&\frac {R_{\mathrm {L}}\beta i_{\mathrm {b}}}{r_{\mathrm {b}}i_{\mathrm {b}}} \\[ 5pt ] &=&\frac {R_{\mathrm {L}}\beta }{r_{\mathrm {b}}} \\[ 5pt ] &=&\frac {9.0\times 10^{3}\times 50 }{15\times 10^{3}} \\[ 5pt ] &=&30 \\[ 5pt ] \end{eqnarray}
\] と求められる。