《理論》〈電気回路〉[H29:問5]直流回路におけるテブナンの定理を用いた解法に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，直流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

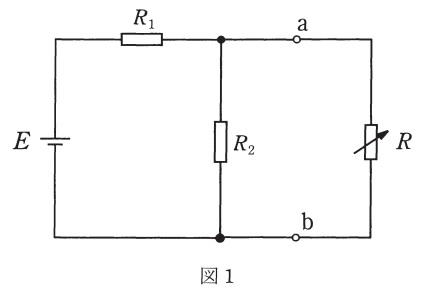
図1に示す直流回路において，電圧$ \ E \ $及び抵抗$ \ R_{1} \ $，$ \ R_{2} \ $の値は固定とし，抵抗$ \ R \ $の値は可変とする。このとき，抵抗$ \ R \ $で消費される最大電力の値を求める。
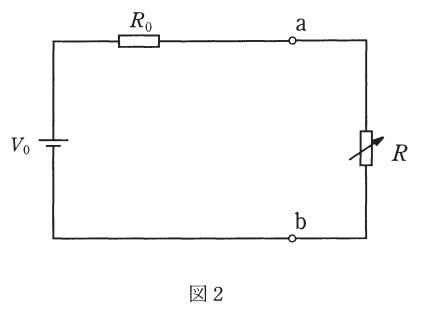
図1の端子$ \ \mathrm {a}-\mathrm {b} \ $から左側の部分を，一つの電圧源と一つの抵抗を用いて等価回路に置き換えると，図2になる。ただし，$ \ V_{0} \ $，$ \ R_{0} \ $は，図1の電圧$ \ E \ $及び抵抗$ \ R_{1} \ $，$ \ R_{2} \ $を用いて，$ \ V_{0}=\fbox {　（１）　} \ $，$ \ R_{0}=\fbox {　（２）　} \ $と表される。
図2において，抵抗$ \ R \ $で消費される電力$ \ P \ $を$ \ V_{0} \ $，$ \ R_{0} \ $，$ \ R \ $を用いて表せば，$ \ P=\fbox {　（３）　} \ $となる。$ \ P \ $が最大となる条件を$ \ V_{0} \ $，$ \ R_{0} \ $，$ \ R \ $を用いて表せば，$ \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}R}=\fbox {　（４）　}=0 \ $となる。
したがって，抵抗$ \ R \ $で消費される最大電力$ \ P_{\mathrm {max}} \ $は，図1の電圧$ \ E \ $及び抵抗$ \ R_{1} \ $，$ \ R_{2} \ $を用いて，$ \ P_{\mathrm {max}}=\fbox {　（５）　} \ $となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　E　　　&（ロ）&　R_{1}　　　&（ハ）&　\frac {{V_{0}}^{2}}{R_{0}} \\[ 5pt ] &（ニ）&　\frac {R_{2}E}{R_{1}+R_{2}}　　　&（ホ）&　R_{1}+R_{2}　　　&（ヘ）&　\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] &（ト）&　\frac {R_{1}E}{R_{1}+R_{2}}　　　&（チ）&　\frac {E^{2}}{4\left( R_{1}+R_{2}\right) }　　　&（リ）&　\frac {\left( R_{0}-R \right) V_{0}^{2}}{\left( R_{0}+R\right) ^{3}} \\[ 5pt ] &（ヌ）&　\frac {\left( R_{0}+R \right) V_{0}^{2}}{\left( R_{0}-R\right) ^{3}}　　　&（ル）&　\frac {\left( R-R_{0} \right) V_{0}^{2}}{\left( R_{0}+R\right) ^{3}}　　　&（ヲ）&　\frac {R_{0}V_{0}^{2}}{\left( R_{0}+R\right) ^{2}} \\[ 5pt ] &（ワ）&　\frac {RV_{0}^{2}}{\left( R_{0}+R\right) ^{2}}　　　&（カ）&　\frac {R_{1}E^{2}}{4R_{2}\left( R_{1}+R_{2}\right) }　　　&（ヨ）&　\frac {R_{2}E^{2}}{4R_{1}\left( R_{1}+R_{2}\right) }
\end{eqnarray}
\]

【ワンポイント解説】

テブナンの定理を用いる必要があるのと，分数の微分の公式を覚えていないと解けません。テブナンの定理は覚えにくい公式の一つですが，頻出の公式となりますので，よく抑えておく必要があります。類題は電験一種や三種でもよくあるので，慣れると$R=R_{0}$の時最大となることが予想できるようになります。オームの法則以外では，本問では以下の公式を使用します。

1.テブナンの定理
　図1において回路中の$ \ 2 \ $端子の電圧を$ \ V_{0} \ $，電圧源を短絡し，電流源を開放した時の端子から見た合成抵抗を$ \ R_{0} \ $とした時，外部抵抗$ \ R \ $とした時，抵抗$ \ R \ $を流れる電流$ \ I \ $は，下式の通りとなります。
\[
\begin{eqnarray}
I&=&\frac {V_{0}}{R+R_{0}} \\[ 5pt ] \end{eqnarray}
\] 　注意：図1の電圧源$ \ E \ $を短絡した回路では，$ \ R_{1} \ $と$ \ R_{2} \ $それぞれの両端の電圧が等しくなるので，回路は並列になります。

2.抵抗で消費される電力
抵抗$ \ R \ $に電流$ \ I \ $が流れている時の消費電力$ \ P \ $は，
\[
\begin{eqnarray}
P&=&RI^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

3.分数の微分
$ \ \displaystyle P\left( R\right)=\frac {u\left( R\right)}{v\left( R\right)} \ $とするとき，
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}R}&=&\frac {u’v-uv’}{v^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　鳳・テブナンの定理の証明

【解答】

(1)解答：ニ
$ \ V_{0} \ $は$ \ E \ $の$ \ R_{1} \ $と$ \ R_{2} \ $の分圧であるから，
\[
\begin{eqnarray}
V_{0}&=&\frac {R_{2}E}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ヘ
テブナンの定理より，$ \ R_{0} \ $は$ \ E \ $を短絡した時の合成抵抗であるから，
\[
\begin{eqnarray}
\frac {1}{R_{0}}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] であり，整理すると，
\[
\begin{eqnarray}
R_{0}&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
図2において，抵抗$ \ R \ $に流れる電流$ \ I \ $は，
\[
\begin{eqnarray}
I&=&\frac {V_{0}}{R_{0}+R} \\[ 5pt ] \end{eqnarray}
\] であるから，抵抗$ \ R \ $で消費される電力$ \ P \ $は，
\[
\begin{eqnarray}
P &=& RI^{2} \\[ 5pt ] &=& R\left( \frac {V_{0}}{R_{0}+R}\right) ^{2} \\[ 5pt ] &=& \frac {RV_{0}^{2}}{\left( R_{0}+R\right) ^{2}}
\end{eqnarray}
\] となる。

(4)解答：リ
ワンポイント解説の「3.分数の微分」より，
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}R} &=& \frac {V_{0}^{2}\left( R_{0}+R\right) ^{2}-RV_{0}^{2}\cdot 2\left( R_{0}+R\right)}{\left( R_{0}+R\right) ^{4}} \\[ 5pt ] &=& \frac {V_{0}^{2}\left( R_{0}+R\right) -2RV_{0}^{2} }{\left( R_{0}+R\right) ^{3}} \\[ 5pt ] &=& \frac {\left( R_{0}-R \right) V_{0}^{2}}{\left( R_{0}+R\right) ^{3}}
\end{eqnarray}
\] となる。

(5)解答：ヨ
$\displaystyle \frac {\mathrm {d}P}{\mathrm {d}R}=0$となる$ \ R \ $は$ \ R=R_{0} \ $の時であるから，これを(3)の解答式に代入すると，
\[
\begin{eqnarray}
P_{\mathrm {max}} &=& \frac {R_{0}V_{0}^{2}}{\left( R_{0}+R_{0}\right) ^{2}} \\[ 5pt ] &=& \frac {R_{0}V_{0}^{2}}{4R_{0}^{2}} \\[ 5pt ] &=& \frac {V_{0}^{2}}{4R_{0}}
\end{eqnarray}
\] となる。さらに上式に$ \ \displaystyle V_{0}=\frac {R_{2}E}{R_{1}+R_{2}} \ $，$ \ \displaystyle R_{0}=\frac {R_{1}R_{2}}{R_{1}+R_{2}} \ $を代入すると，
\[
\begin{eqnarray}
P_{\mathrm {max}} &=& \frac {\displaystyle \left( \frac {R_{2}E}{R_{1}+R_{2}}\right) ^{2}}{\displaystyle 4\left( \frac {R_{1}R_{2}}{R_{1}+R_{2}}\right) } \\[ 5pt ] &=& \frac {R_{2}E^{2}}{4R_{1}\left( R_{1}+R_{2}\right) }
\end{eqnarray}
\] と求められる。