《理論》〈電磁気〉[H26:問5]環状ソレノイドの磁束の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，環状ソレノイドに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。

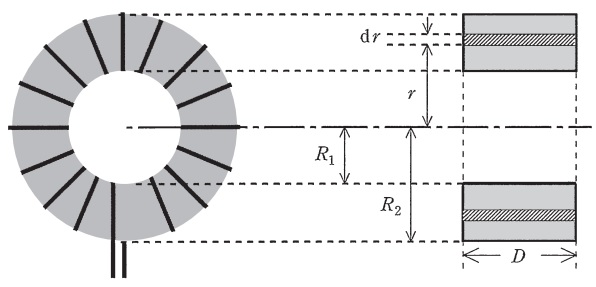
図に示すように，内半径\( \ R_{1} \ \)，外半径\( \ R_{2} \ \)，厚さ\( \ D \ \)の長方形断面をもつ環状鉄心に，総巻数\( \ N \ \)の導線を巻いた環状ソレノイドを考える。このとき，鉄心の比透磁率を\( \ \mu _{\mathrm {r}} \ \)，真空の透磁率を\( \ \mu _{0} \ \)とする。

環状ソレノイドに電流\( \ I \ \)を流したとき，環状鉄心の中心軸から半径\( \ r \ ( R_{1} ＜ r ＜ R_{2} ) \ \)の位置での磁界\( \ H \ \)は\( \ \fbox {　 （１） 　} \ \)である。よって，半径\( \ r \ \)の位置の微小部分\( \ \mathrm {d} r \ \)の部分を通る磁束\( \ \mathrm {d} \mathit {\Phi} _{\mathrm {B}} \ \)は\( \ \fbox {　 （２） 　} \ \)である。

これを\( \ R_{1} \ \)から\( \ R_{2} \ \)まで積分することにより，全磁束\( \ \mathit {\Phi} _{\mathrm {B}} \ \)は\( \ \fbox {　 （３） 　} \ \)と求まる。

鎖交磁束\( \ \mathit {\Phi} \ \)は磁束\( \ \mathit {\Phi} _{\mathrm {B}} \ \)を用いて\( \ N\mathit {\Phi} _{\mathrm {B}} \ \)と表され，電流\( \ I \ \)とインダクタンス\( \ L \ \)を用いると\( \ \mathit {\Phi} =\fbox {　 （４） 　} \ \)の関係があることから，インダクタンス\( \ L \ \)は\( \ \fbox {　 （５） 　} \ \)と求まる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\mu _{\mathrm {r}}NI}{2\pi r}　　　&（ロ）&　\frac {\mu _{\mathrm {r}}\mu _{0}NID}{2\pi }\ln \left( R_{2} -R_{1} \right) 　　　&（ハ）&　\frac {NI}{4\pi r} \\[ 5pt ] &（ニ）&　LI　　　&（ホ）&　\frac {\mu _{\mathrm {r}}\mu _{0}N^{2}D}{2\pi }\left( R_{2} -R_{1} \right) 　　　&（ヘ）&　\frac {\mu _{\mathrm {r}}\mu _{0}ND}{2I\pi }\ln \frac {R_{2}}{R_{1}} \\[ 5pt ] &（ト）&　\frac {\mu _{\mathrm {r}}\mu _{0}NID}{2\pi }\ln \frac {R_{2}}{R_{1}}　　　&（チ）&　\frac {\mu _{\mathrm {r}}\mu _{0}N^{2}D}{2\pi }\ln \frac {R_{2}}{R_{1}}　　　　&（リ）&　\frac {NI}{2\pi r} \\[ 5pt ] &（ヌ）&　\frac {I}{L}　　　&（ル）&　\frac {LI^{2}}{2}　　　&（ヲ）&　\frac {\mu _{\mathrm {r}}\mu _{0}NID}{2\pi r}\mathrm {d}r \\[ 5pt ] &（ワ）&　\frac {\mu _{\mathrm {r}}\mu _{0}NID}{2\pi }\left( R_{2} -R_{1} \right)　　　&（カ）&　\frac {\mu _{\mathrm {r}}\mu _{0}NID}{4\pi r}\mathrm {d}r　　　&（ヨ）&　\frac {\mu _{\mathrm {r}}NID}{2\pi r}\mathrm {d}r \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

環状ソレノイドの鎖交磁束の導出に関する問題です。難易度もそれほど高くなく，基本的な積分とソレノイドの磁束の導出方法を理解するのには非常に良い問題です。三種よりさらに高度になった問題をマスターできるようにしましょう。

1.環状ソレノイドの内部の磁界\( \ H \ \)
巻数\( \ N \ \)，電流\( \ I \ \)，平均磁路長\( \ l \ \)の環状ソレノイドの内部鉄心の磁界の強さ\( \ H \ \)は，アンペアの周回積分の法則により，
\[
\begin{eqnarray}
\Sigma I &=& \int _{\mathrm {c}} \boldsymbol H \cdot d\boldsymbol l \\[ 5pt ] NI &=& Hl \\[ 5pt ] H &=& \frac {NI}{l} \\[ 5pt ] \end{eqnarray}
\] と求められます。

2.環状ソレノイドの内部の磁束\( \ \mathit {\Phi } \ \)
環状ソレノイドの磁束密度\( \ B \ \)は，鉄心中の透磁率を\( \ \mu \ \)とすると，
\[
\begin{eqnarray}
B &=& \mu H \\[ 5pt ] &=& \frac {\mu NI}{l} \\[ 5pt ] \end{eqnarray}
\] となるから，ソレノイド内部の磁束\( \ \mathit {\Phi } \ \)は，ソレノイドの断面積を\( \ S \ \)とすると，
\[
\begin{eqnarray}
\mathit {\Phi } &=& BS \\[ 5pt ] &=& \frac {\mu NIS}{l} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：リ
環状鉄心の中心軸から距離\( \ r \ \)での磁路長\( \ l \ \)は，\( \ l=2\pi r \ \)であるから，ワンポイント解説「1.環状ソレノイドの内部の磁界\( \ H \ \)」より，磁界\( \ H \ \)は，
\[
\begin{eqnarray}
NI &=& H\cdot 2\pi r \\[ 5pt ] H &=& \frac {NI}{2\pi r } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヲ
微小区間における磁束密度\( \ B \ \)は，
\[
\begin{eqnarray}
B &=& \mu _{\mathrm {r}}\mu _{0} H \\[ 5pt ] &=& \frac {\mu _{\mathrm {r}}\mu _{0} NI}{2\pi r } \\[ 5pt ] \end{eqnarray}
\] であり，半径\( \ r \ \)の場所での微小区間の断面積\( \ \mathrm {d}S \ \)は，
\[
\begin{eqnarray}
\mathrm {d}S &=& D\mathrm {d}r \\[ 5pt ] \end{eqnarray}
\] であるから，微小区間を通る磁束\( \ \mathrm {d}\mathit {\Phi _{\mathrm {B}}} \ \)は，
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi _{\mathrm {B}}} &=& B\mathrm {d}S \\[ 5pt ] &=& \frac {\mu _{\mathrm {r}}\mu _{0} NID}{2\pi r } \mathrm {d}r \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ト
(2)の解答式において，\( \ r \ \)を\( \ R_{1} \ \)から\( \ R_{2} \ \)まで積分すると，
\[
\begin{eqnarray}
\mathit {\Phi _{\mathrm {B}}} &=& \int _{R_{1}}^{R_{2}} \frac {\mu _{\mathrm {r}}\mu _{0} NID}{2\pi r } \mathrm {d}r \\[ 5pt ] &=& \frac {\mu _{\mathrm {r}}\mu _{0} NID}{2\pi } \int _{R_{1}}^{R_{2}} \frac {1}{r} \mathrm {d}r \\[ 5pt ] &=& \frac {\mu _{\mathrm {r}}\mu _{0} NID}{2\pi } \left[ \ln r \right] _{R_{1}}^{R_{2}} \\[ 5pt ] &=& \frac {\mu _{\mathrm {r}}\mu _{0} NID}{2\pi } \left[ \ln R_{2}-\ln R_{1} \right] \\[ 5pt ] &=& \frac {\mu _{\mathrm {r}}\mu _{0} NID}{2\pi } \ln \frac {R_{2}}{R_{1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ニ
鎖交磁束\( \ \mathit {\Phi} \ \)は磁束\( \ \mathit {\Phi} _{\mathrm {B}} \ \)を用いて\( \ N\mathit {\Phi} _{\mathrm {B}} \ \)と表され，電流\( \ I \ \)とインダクタンス\( \ L \ \)を用いると\( \ \mathit {\Phi} =LI \ \)の関係がある。

(5)解答：チ
(3)，(4)より，
\[
\begin{eqnarray}
\mathit {\Phi} &=& LI\\[ 5pt ] N\mathit {\Phi} _{\mathrm {B}}&=& LI \\[ 5pt ] \frac {\mu _{\mathrm {r}}\mu _{0} N^{2}ID}{2\pi } \ln \frac {R_{2}}{R_{1}}&=& LI \\[ 5pt ] L&=&\frac {\mu _{\mathrm {r}}\mu _{0} N^{2}D}{2\pi } \ln \frac {R_{2}}{R_{1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。