《理論》〈電気回路〉[H27:問2]交流回路の電流及び電圧の計算方法に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，交流回路の電流及び電圧の計算方法に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。

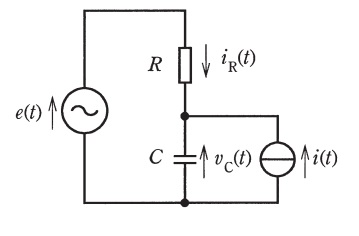
図の回路において，重ね合わせの理(重ねの理)を用いて，抵抗に流れる電流\( \ i_{\mathrm {R}}(t) \ \)，キャパシタの両端の電圧\( \ v_{\mathrm {C}}(t) \ \)を求めたい。

ただし，交流電圧源\( \ e(t)=E_{\mathrm {m}}\cos \omega _{1} t \ \)，交流電流源\( \ i(t)=I_{\mathrm {m}}\sin \omega _{2} t \ \)とする。

抵抗に流れる電流\( \ i_{\mathrm {R}}(t) \ \)は，電流の向きを考えると，
\[
i_{\mathrm {R}}(t)=I_{\mathrm {e}}\cos (\omega _{1}t+\varphi _{\mathrm {e}})-I_{\mathrm {i}}\sin (\omega _{2}t+\varphi _{\mathrm {i}})
\] と表すことが出来る。電圧源のみで考えると，\( \ I_{\mathrm {e}}=\fbox {　 （１） 　} \ \)，電流源のみで考えると\( \ I_{\mathrm {i}}=\fbox {　 （２） 　} \ \)となる。

同様に，キャパシタの両端の電圧\( \ v_{\mathrm {C}}(t) \ \)を，電圧源，電流源それぞれについて求めると，
\[
v_{\mathrm {C}}(t)=V_{\mathrm {e}}\cos (\omega _{1}t+\phi _{\mathrm {e}})+V_{\mathrm {i}}\sin (\omega _{2}t+\phi _{\mathrm {i}})
\] と表すことができる。ここで，\( \ \displaystyle -\frac {\pi }{2} ＜ \phi _{\mathrm {e}} ＜ \frac {\pi }{2} \ \)とする。

このとき，\( \ V_{\mathrm {e}}=\fbox {　 （３） 　} \ \)，\( \ \phi _{\mathrm {e}}=\fbox {　 （４） 　} \ \)，\( \ V_{\mathrm {i}}=\fbox {　 （５） 　} \ \)となる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\omega _{1}CE_{\mathrm {m}}}{1+\omega _{1}CR}　　　&（ロ）&　\frac {\omega _{2}CRI_{\mathrm {m}}}{\sqrt {1+\left( \omega _{2}CR\right) ^{2}}}　　　&（ハ）&　\frac {\pi }{2}-\tan ^{-1}\omega _{1}CR \\[ 5pt ] &（ニ）&　\frac {RI_{\mathrm {m}}}{\sqrt {1+\left( \omega _{2}CR\right) ^{2}}}　　　&（ホ）&　\frac {\omega _{1}CE_{\mathrm {m}}}{\sqrt {1+\left( \omega _{1}CR\right) ^{2}}}　　　&（ヘ）&　\omega _{1}CE_{\mathrm {m}} \\[ 5pt ] &（ト）&　\frac {E_{\mathrm {m}}}{R}　　　&（チ）&　\frac {I_{\mathrm {m}}}{\sqrt {1+\left( \omega _{2}CR\right) ^{2}}}　　　　&（リ）&　\frac {I_{\mathrm {m}}}{\omega _{2}C} \\[ 5pt ] &（ヌ）&　\frac {I_{\mathrm {m}}}{1+\omega _{2}CR}　　　&（ル）&　-\tan ^{-1}\frac {1}{\omega _{1}CR}　　　&（ヲ）&　\frac {RI_{\mathrm {m}}}{1+\omega _{2}CR} \\[ 5pt ] &（ワ）&　\frac {E_{\mathrm {m}}}{\sqrt {1+\left( \omega _{1}CR\right) ^{2}}}　　　&（カ）&　\frac {E_{\mathrm {m}}}{1+\omega _{1}CR}　　　&（ヨ）&　-\tan ^{-1}\omega _{1}CR
\end{eqnarray}
\]

【ワンポイント解説】

重ね合わせの理を用いて解く問題です。重ね合わせの理は３種の頃からよく出題されていた問題であると思います。２種になると内容は少し高度になりますが，考え方は同じです。確実に使いこなせるようにしておきましょう。

1.重ね合わせの理(重ねの理)
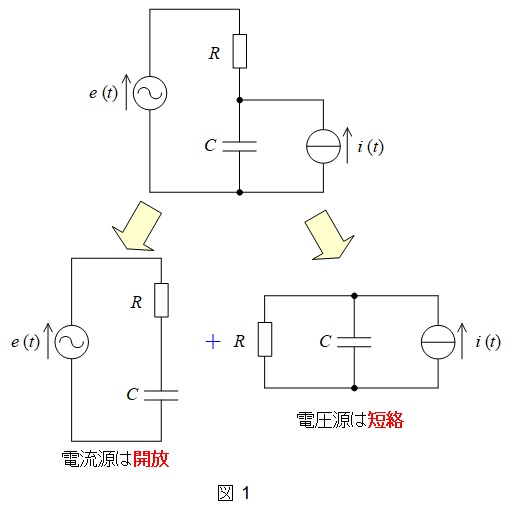
複数の電源で構成された回路は，電源毎に計算した電流を重ね合わせて求めることができます。この時，電圧源は短絡，電流源は開放します。問題に対する回路は図1のようになります。

【関連する「電気の神髄」記事】

　　重ね合わせの理の証明

【解答】

(1)解答：ホ
図1の左図より，電圧源から\( \ E_{\mathrm {m}} \ \)の電圧がかかった時の\( \ {\dot I}_{\mathrm {e}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {e}} &=& \frac {E_{\mathrm {m}}}{R+\frac {1}{\mathrm {j}\omega _{1}C}} \\[ 5pt ] &=& \frac {\mathrm {j}\omega _{1}CE_{\mathrm {m}}}{1+\mathrm {j}\omega _{1}CR}
\end{eqnarray}
\] となるので，その大きさ\( \ I_{\mathrm {e}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {e}} &=& \left| \frac {\mathrm {j}\omega _{1}CE_{\mathrm {m}}}{1+\mathrm {j}\omega _{1}CR}\right| \\[ 5pt ] &=& \frac {\omega _{1}CE_{\mathrm {m}}}{\sqrt {1+\left( \omega _{1}CR\right) ^{2}}}
\end{eqnarray}
\] と求められる。

(2)解答：チ
図1の右図より，電流源から\( \ I_{\mathrm {m}} \ \)の電流が流れた時の\( \ {\dot I}_{\mathrm {i}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {i}} &=& \frac {\frac {1}{\mathrm {j}\omega _{2}C}}{R+\frac {1}{\mathrm {j}\omega _{2}C}}I_{\mathrm {m}} \\[ 5pt ] &=& \frac {I_{\mathrm {m}}}{1+\mathrm {j}\omega _{2}CR}
\end{eqnarray}
\] となるので，その大きさ\( \ I_{\mathrm {i}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {i}} &=& \left| \frac {I_{\mathrm {m}}}{1+\mathrm {j}\omega _{2}CR}\right| \\[ 5pt ] &=& \frac {I_{\mathrm {m}}}{\sqrt {1+\left( \omega _{2}CR\right) ^{2}}}
\end{eqnarray}
\] と求められる。

(3)解答：ワ
電圧源から\( \ E_{\mathrm {m}} \ \)の電圧がかかった時のキャパシタの電圧\( \ {\dot V}_{\mathrm {e}} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {e}} &=& \frac {\frac {1}{\mathrm {j}\omega _{1}C}}{R+\frac {1}{\mathrm {j}\omega _{1}C}}E_{\mathrm {m}} \\[ 5pt ] &=& \frac {E_{\mathrm {m}}}{1+\mathrm {j}\omega _{1}CR}
\end{eqnarray}
\] となるので，その大きさ\( \ V_{\mathrm {e}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {e}} &=& \left| \frac {E_{\mathrm {m}}}{1+\mathrm {j}\omega _{1}CR}\right| \\[ 5pt ] &=& \frac {E_{\mathrm {m}}}{\sqrt {1+\left( \omega _{1}CR\right) ^{2}}}
\end{eqnarray}
\] と求められる。

(4)解答：ヨ
(3)より，\( \ {\dot V}_{\mathrm {e}} \ \)を変形すると，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {e}} &=& \frac {E_{\mathrm {m}}}{1+\mathrm {j}\omega _{1}CR} \\[ 5pt ] &=& \frac {E_{\mathrm {m}}}{1+\left( \omega _{1}CR\right) ^{2}}(1-\mathrm {j}\omega _{1}CR)
\end{eqnarray}
\] となるので，\( \ \phi _{\mathrm {e}} \ \)は，
\[
\begin{eqnarray}
\phi _{\mathrm {e}} &=& \tan ^{-1} \frac {-\omega _{1}CR}{1} \\[ 5pt ] &=&-\tan ^{-1} \omega _{1}CR
\end{eqnarray}
\] と求められる。

(5)解答：ニ
図1右図より，電流源から\( \ I_{\mathrm {m}} \ \)の電流が流れた時のキャパシタに現れる電圧\( \ V_{\mathrm {i}} \ \)は抵抗に現れる電圧と等しいので，
\[
\begin{eqnarray}
V_{\mathrm {i}} &=& RI_{\mathrm {i}} \\[ 5pt ] &=& R\cdot \frac {I_{\mathrm {m}}}{\sqrt {1+\left( \omega _{2}CR\right) ^{2}}} \\[ 5pt ] &=&\frac {RI_{\mathrm {m}}}{\sqrt {1+\left( \omega _{2}CR\right) ^{2}}}
\end{eqnarray}
\] と求められる。