《理論》〈電磁気〉[H27:問5]単相変圧器の特性計算に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，変圧器に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

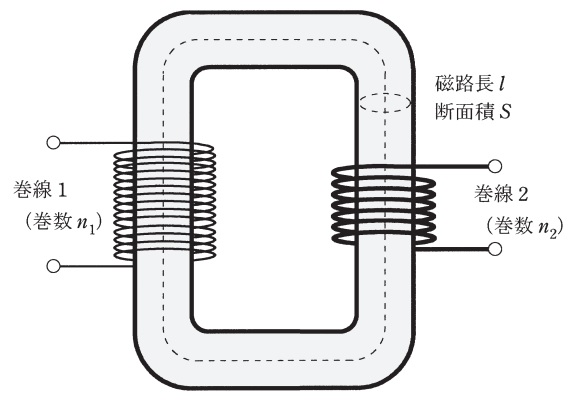
図に示すような単相変圧器がある。ここで，鉄心の比透磁率を$ \ \mu _{\mathrm {r}} \ $，磁路長を$ \ l \ $，断面積を$ \ S \ $とし，巻数が$ \ n_{1} \ $の巻線$ \ 1 \ $と巻数が$ \ n_{2} \ $の巻線$ \ 2 \ $が巻かれている。また，真空の透磁率を$ \ \mu _{0} \ $とし，磁束の漏れは無視できるものとする。

巻線$ \ 1 \ $に周波数$ \ f \ $の交流電流$ \ i \ $を流したとき，鉄心の磁気回路を考えることで，鉄心中の磁束$ \ \mathit {\Phi } \ $は$ \ \mathit {\Phi } =\fbox {　（１）　} \ $と表される。

鉄心中の磁束$ \ \mathit {\Phi } \ $を用いると，巻線$ \ 2 \ $に発生する起電力$ \ U \ $は$ \ U=\fbox {　（２）　} \ $と表される。

例えば，交流電流の周波数を$ \ 50 \ \mathrm {Hz} \ $，実効値を$ \ 1 \ \mathrm {A} \ $とすると，交流電流$ \ i \ $は三角関数を用いて$ \ i= \ \fbox {　（３）　} \ \sin \left( \ \fbox {　（４）　} \ t\right) \ \mathrm {[A]} \ $と表すことができるため，$ \ \mathit {\Phi }= \ \fbox {　（１）　} \ $と$ \ U=\fbox {　（２）　} \ $の関係を用いて，巻線$ \ 2 \ $の両端に発生する電圧を求めることができる。

例えば，$ \ n_{1}=100 \ $，$ \ n_{2}=20 \ $，$ \ \mu _{0} =4\pi \times 10^{-7} \ \mathrm {[H/m]} \ $，$ \ \mu _{\mathrm {r}}=1 \ 000 \ $，$ \ S=3.0\times 10^{-3} \ \mathrm {m^{2}} \ $，$ \ l=0.5 \ \mathrm {m} \ $とすると，巻線$ \ 2 \ $の両端には実効値で$ \ \fbox {　（５）　} \ \mathrm {V} \ $の電圧が発生することになる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　-n_{2}\frac {\mathrm {d}^{2}\mathit {\Phi}}{{\mathrm {d}t}^{2}}　　　&（ロ）&　\frac {n_{1}i\mu _{0} \mu _{\mathrm {r}}S}{2\pi l}　　　&（ハ）&　\frac {n_{1}i\mu _{0} \mu _{\mathrm {r}}S}{l} \\[ 5pt ] &（ニ）&　\sqrt {2}　　　&（ホ）&　4.73　　　&（ヘ）&　2 \\[ 5pt ] &（ト）&　3.46　　　&（チ）&　-n_{2}{\mathit {\Phi}}^{2}　　　　&（リ）&　100\pi \\[ 5pt ] &（ヌ）&　50　　　&（ル）&　\frac {n_{1}i\mu _{0} \mu _{\mathrm {r}}S}{2\pi l^{2}}　　　&（ヲ）&　2.82 \\[ 5pt ] &（ワ）&　-n_{2}\frac {\mathrm {d}\mathit {\Phi}}{\mathrm {d}t}　　　&（カ）&　\sqrt {3}　　　&（ヨ）&　50\pi
\end{eqnarray}
\]

【ワンポイント解説】

変圧器に関する問題で，内容はそれほど複雑ではありませんが，高い計算能力が求められる問題となっています。

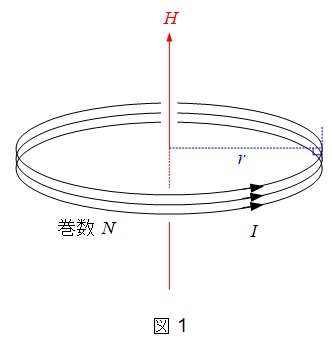
1.アンペールの法則
図1の示すような，電流$I$が流れているコイルの中心に発生する磁界の大きさ$H$は，
\[
NI=\int H\cdot \mathrm {d}l
\] となります。

2.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係
透磁率が$ \ \mu \ $の時，磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係は，
\[
B=\mu H
\] となります。

3.磁束$ \ \mathit {\Phi } \ $と磁束密度$ \ B \ $の関係
断面積が$ \ S \ $，磁束密度$ \ B \ $が与えられているとき，磁束$ \ \mathit {\Phi } \ $の大きさは，
\[
\mathit {\Phi }=\int B\cdot \mathrm {d}S
\] となります。

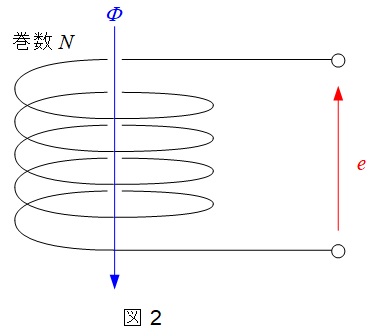
4.電磁誘導に関するファラデーの法則
図2に示すような巻線$ \ N \ $のコイルに磁束$ \ \mathit {\Phi } \ $が通過している時，発生する誘導起電力$ \ e \ $は，
\[
\begin{eqnarray}
e&=&-N\frac {\mathrm {d}\mathit {\Phi }}{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] となります。式についている－の符号は変化する磁束を打ち消す方向に誘導起電力が発生するという意味です。

【解答】

(1)解答：ハ
ワンポイント解説「1.アンペールの法則」より，巻線$1$に周波数$f$の交流電流$i$を流したとき，鉄心の磁気回路中に発生する磁界の大きさ$ \ H \ $は，
\[
\begin{eqnarray}
n_{1}i&=& Hl \\[ 5pt ] H&=& \frac {n_{1}i}{l} \\[ 5pt ] \end{eqnarray}
\] となる。よって，鉄心中の磁束密度$ \ B \ $は，ワンポイント解説「2.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係」より，
\[
\begin{eqnarray}
B&=& \mu H \\[ 5pt ] &=& \mu _{0} \mu _{\mathrm {r}} \frac {n_{1}i}{l} \\[ 5pt ] &=& \frac {n_{1}i\mu _{0} \mu _{\mathrm {r}}}{l} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「3.磁束$ \ \mathit {\Phi } \ $と磁束密度$ \ B \ $の関係」より，断面積が$ \ S \ $であるから，
\[
\begin{eqnarray}
\mathit {\Phi }&=& BS \\[ 5pt ] &=& \frac {n_{1}i\mu _{0} \mu _{\mathrm {r}}}{l} S \\[ 5pt ] &=& \frac {n_{1}i\mu _{0} \mu _{\mathrm {r}}S}{l} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ワ
ワンポイント解説「4.電磁誘導に関するファラデーの法則」より，巻線$ \ 2 \ $に発生する誘導起電力$ \ U \ $は，
\[
U=-n_{2}\frac {\mathrm {d}\mathit {\Phi}}{\mathrm {d}t}
\] と求められる。

(3)解答：ニ
正弦波において，波高値は実効値の$ \ \sqrt {2} \ $倍であるから，$ \ \sqrt {2} \ \mathrm {[A]} \ $と求められる。

(4)解答：リ
交流電流は$ \ i=A\sin \omega t \ $で表せ，$ \ \omega =2\pi f \ $であるから，
\[
\begin{eqnarray}
\omega &=& 2\pi f \\[ 5pt ] &=& 2\pi \times 50 \\[ 5pt ] &=& 100 \pi \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
\[
\begin{eqnarray}
\mathit {\Phi } &=& \frac {n_{1}i\mu _{0} \mu _{\mathrm {r}}S}{l} \\[ 5pt ] &=& \frac {n_{1}\mu _{0} \mu _{\mathrm {r}}S}{l}\sqrt {2}\sin \left( 100 \pi t\right) \\[ 5pt ] &=& \frac {\sqrt {2} n_{1}\mu _{0} \mu _{\mathrm {r}}S}{l}\sin \left( 100 \pi t\right) \\[ 5pt ] \end{eqnarray}
\] より，
\[
\begin{eqnarray}
\frac {\mathrm {d}\mathit {\Phi }}{\mathrm {d}t} &=& \frac {\sqrt {2} n_{1}\mu _{0} \mu _{\mathrm {r}}S}{l} \frac {\mathrm {d}}{\mathrm {d}t}\left[ \sin \left( 100 \pi t\right) \right] \\[ 5pt ] &=& \frac {100\sqrt {2}\pi n_{1}\mu _{0} \mu _{\mathrm {r}}S}{l}\cos \left( 100 \pi t\right) \\[ 5pt ] \end{eqnarray}
\] となるので，誘導起電力$ \ U \ $は，
\[
\begin{eqnarray}
U &=&-n_{2}\frac {\mathrm {d}\mathit {\Phi}}{\mathrm {d}t} \\[ 5pt ] &=&-n_{2}\frac {100\sqrt {2}\pi n_{1}\mu _{0} \mu _{\mathrm {r}}S}{l}\cos \left( 100 \pi t\right) \\[ 5pt ] &=&- \frac {100\sqrt {2}\pi n_{1}n_{2}\mu _{0} \mu _{\mathrm {r}}S}{l}\cos \left( 100 \pi t\right) \\[ 5pt ] \end{eqnarray}
\] となるので，誘導起電力$ \ U \ $の実効値$ \ U_{\mathrm {d}} \ $は，
\[
\begin{eqnarray}
U_{\mathrm {d}} &=&\frac {100\pi n_{1}n_{2}\mu _{0} \mu _{\mathrm {r}}S}{l} \\[ 5pt ] &=&\frac {100\pi \times 100\times 20\times 4\pi \times 10^{-7} \times 1000 \times 3.0\times 10^{-3}}{0.5} \\[ 5pt ] &≒& 4.73 \ \mathrm {[V]}
\end{eqnarray}
\] と求められる。