【問題】
【難易度】★★★☆☆(普通)
次の文章は,接地抵抗計に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選びなさい。
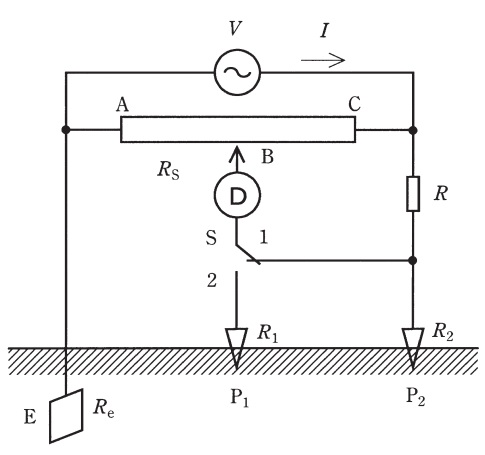
図のように,測定対象の接地電極を\(\mathrm {E}\),補助電極を\(\mathrm {P_{1}}\)及び\(\mathrm {P_{2}}\)とし,その接地抵抗値をそれぞれ\(R_{\mathrm {e}}\),\(R_{1}\)及び\(R_{2}\)とする。また,交流電源の電圧を\(V\),固定抵抗器の抵抗値を\(R\),滑り抵抗器の抵抗値(\(\mathrm {A-C}\)間)を\(R_{\mathrm {S}}\)とする。ただし,各電極は互いに影響がないように十分離して接地されている。
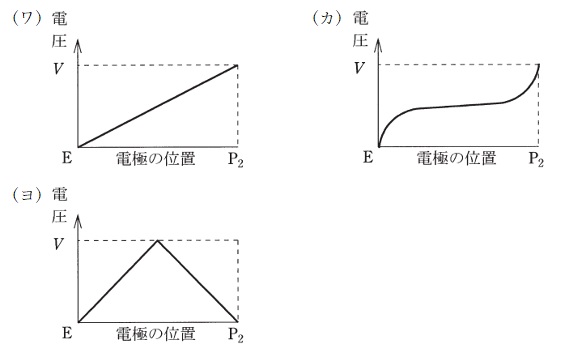
図に示す接地抵抗値の測定において,電流\(I\)が図のように流れ,スイッチ\(\mathrm {S}\)が1側に閉じているときの電極\(\mathrm {E}\)及び\(\mathrm {P_{2}}\)間の地中の電位分布を図に表すと\(\fbox { (1) }\)のようになる。
いま,スイッチ\(\mathrm {S}\)を1側に閉じ,滑り抵抗器の\(\mathrm {A-B}\)間の抵抗値が\(r_{1}\),\(\mathrm {B-C}\)間の抵抗値が\(r_{2}\)を示したときに検出器Ⓓの読みが零になり回路が平衡したとすれば,①式が得られる。
\[
r_{1}R=\fbox { (2) } ・・・・・・・・・・ ①
\]
次に,スイッチ\(\mathrm {S}\)を2側に閉じ,同様に滑り抵抗器の\(\mathrm {A-B}\)間の抵抗値が\(r_{3}\),\(\mathrm {B-C}\)間の抵抗値が\(r_{4}\)を示したときに回路が平衡したとすれば,②式が得られる。
\[
r_{4}R_{\mathrm {e}}=\fbox { (3) } \ ・・・・・・・・・ ②
\]
以上の測定から,①式及び②式より\(R_{2}\)を消去して接地抵抗値\(R_{\mathrm {e}}\)を求めれば,\(r_{1}\),\(r_{2}\),\(r_{3}\),\(r_{4}\)及び\(\fbox { (4) }\)の値を用いて,\(R_{\mathrm {e}}=\fbox { (5) }\)となる。
ただし,\(r_{1}+r_{2}=r_{3}+r_{4}=R_{\mathrm {S}}\)である。
〔問8の解答群〕
\[
\begin{eqnarray}
&(イ)& R &(ロ)& r_{2}\left( R_{\mathrm {e}}+R_{2}\right) &(ハ)& R_{1} \\[ 5pt ]
&(ニ)& r_{2}\left( R_{1}+R_{2}\right) &(ホ)& \displaystyle \frac {r_{3}}{r_{2}}R_{1} &(ヘ)& \displaystyle \frac {r_{3}}{r_{2}}R \\[ 5pt ]
&(ト)& r_{3}\left( R_{1}+R_{2}\right) &(チ)& r_{1}R_{2} &(リ)& \displaystyle \frac {R_{2}}{R_{1}} \\[ 5pt ]
&(ヌ)& r_{3}\left( R_{2}+R\right) &(ル)& \displaystyle \frac {r_{4}}{r_{2}}R &(ヲ)& r_{3}R_{2} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
接地抵抗計に関する問題で,実際に建設所で接地抵抗測定をする際も似たような方法で測定します。そのメカニズムを理解するのには非常に良い問題となりますので,理解しておくようにしましょう。
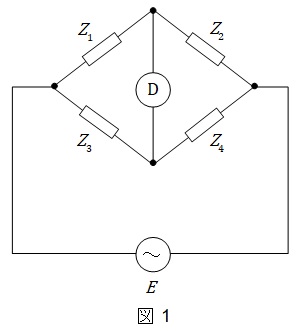
1.交流ブリッジ回路の平衡条件
図1の回路において,検流計に電流が流れない条件(平衡条件)は,
\[
Z_{1}Z_{4}=Z_{2}Z_{3}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)解答:カ
電極近傍での電位は電極からの距離に反比例するので,\(\mathrm {P_{2}}\)では反比例に近い形,\(\mathrm {E}\)は反比例をひっくり返したような形になる。よって,(カ)の波形となる。
(2)解答:ロ
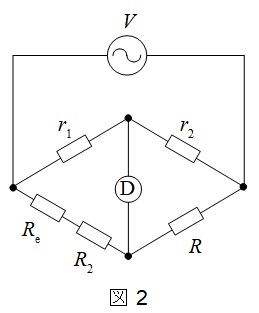
スイッチ\(\mathrm {S}\)を1側に閉じ,滑り抵抗器の\(\mathrm {A-B}\)間の抵抗値が\(r_{1}\),\(\mathrm {B-C}\)間の抵抗値が\(r_{2}\)を示したときの等価回路を図2に示す。
ワンポイント解説「1.交流ブリッジ回路の平衡条件」より,
\[
r_{1}R=r_{2}\left( R_{\mathrm {e}}+R_{2}\right)
\]
と求められる。
(3)解答:ヌ
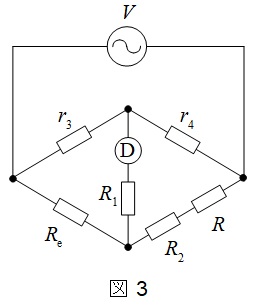
スイッチ\(\mathrm {S}\)を2側に閉じ,滑り抵抗器の\(\mathrm {A-B}\)間の抵抗値が\(r_{3}\),\(\mathrm {B-C}\)間の抵抗値が\(r_{4}\)を示したときの等価回路を図3に示す。
ワンポイント解説「1.交流ブリッジ回路の平衡条件」より,
\[
r_{4}R_{\mathrm {e}}=r_{3}\left( R_{2}+R\right)
\]
と求められる。
(4)解答:イ
(5)解答:ヘ
①,②式を\(R_{2}\)について整理すると,
\[
\begin{eqnarray}
r_{1}R&=&r_{2}\left( R_{\mathrm {e}}+R_{2}\right) \\[ 5pt ]
R_{2}&=&\frac {r_{1}R-r_{2}R_{\mathrm {e}}}{r_{2}} ・・・・・・・ ①^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
及び
\[
\begin{eqnarray}
r_{4}R_{\mathrm {e}}&=&r_{3}\left( R_{2}+R\right) \\[ 5pt ]
R_{2}&=&\frac {r_{4}R_{\mathrm {e}}-r_{3}R}{r_{3}} ・・・・・・ ②^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\(R_{2}\)を消去すると,
\[
\begin{eqnarray}
\frac {r_{1}R-r_{2}R_{\mathrm {e}}}{r_{2}}&=&\frac {r_{4}R_{\mathrm {e}}-r_{3}R}{r_{3}} \\[ 5pt ]
r_{1}r_{3}R-r_{2}r_{3}R_{\mathrm {e}}&=&r_{2}r_{4}R_{\mathrm {e}}-r_{2}r_{3}R \\[ 5pt ]
r_{2}\left( r_{3}+r_{4}\right) R_{\mathrm {e}}&=&r_{3}\left( r_{1}+r_{2}\right) R \\[ 5pt ]
R_{\mathrm {e}}&=&\frac {r_{3}\left( r_{1}+r_{2}\right) }{r_{2}\left( r_{3}+r_{4}\right) } R \\[ 5pt ]
\end{eqnarray}
\]
となるので,題意より\(r_{1}+r_{2}=r_{3}+r_{4}=R_{\mathrm {S}}\)であるので,
\[
R_{\mathrm {e}}=\frac {r_{3}}{r_{2}} R
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは