《理論》〈電気回路〉[H28:問6] 交流回路における位相の関係に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。

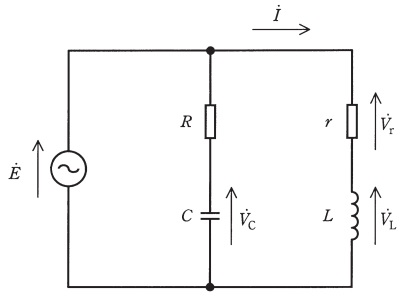
図の回路において交流電圧源\( \ \dot E \ \)の角周波数は\( \ \omega \ \)とする。それぞれの素子の両端の電圧と，素子に流れる電流を求めたい。
抵抗\( \ r \ \)に流れる電流\( \ \dot I \ \)は，
\[
\begin{eqnarray}
\dot I &=& \ \fbox {　 （１） 　}　\\[ 5pt ] \end{eqnarray}
\] インダクタンス\( \ L \ \)のコイルの両端の電圧\( \ {\dot V}_{\mathrm{L}} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm{L}} &=& \ \fbox {　 （２） 　}　\\[ 5pt ] \end{eqnarray}
\] 静電容量\( \ C \ \)のコンデンサの両端の電圧\( \ {\dot V}_{\mathrm{C}} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm{C}} &=& \ \fbox {　 （３） 　}　\\[ 5pt ] \end{eqnarray}
\] となる。
各素子の値が\( \ \fbox {　 （４） 　} \ \)の関係にあるとき，\( \ \omega \ \)の値に関係なく\( \ {\dot V}_{\mathrm{C}}={\dot V}_{\mathrm{r}} \ \)となる。このとき，\( \ {\dot V}_{\mathrm{C}} \ \)の位相は\( \ {\dot V}_{\mathrm{L}} \ \)に対して，\( \ \fbox {　 （５） 　} \ \)。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\mathrm {j}\omega L}{r+\mathrm {j}\omega L}\dot E　　　&（ロ）&　\frac {1}{\mathrm {j}\omega L}\dot E　　　&（ハ）&　Rr=\sqrt {LC} \\[ 5pt ] &（ニ）&　\frac {\mathrm {j}\omega L}{r}\dot E　　　&（ホ）&　\frac {R}{1+\mathrm {j}\omega CR}\dot E　　　&（ヘ）&　\frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}\dot E \\[ 5pt ] &（ト）&　\frac {1}{r+\mathrm {j}\omega L}\dot E　　　&（チ）&　\frac {1}{1+\mathrm {j}\omega CR}\dot E 　　　&（リ）&　\frac {r}{r+\mathrm {j}\omega L}\dot E \\[ 5pt ] &（ヌ）&　Rr=\frac {C}{L}　　　&（ル）&　\frac {1}{r}\dot E　　　&（ヲ）&　Rr=\frac {L}{C}　 \\[ 5pt ] &（ワ）&　同相である　　　&（カ）&　90°遅れている　　　&（ヨ）&　90°進んでいる
\end{eqnarray}
\]

【ワンポイント解説】

交流回路ではコンデンサでは電流の位相が90°進み，インダクタンスでは電流の位相が\( \ 90° \ \)遅れるという特性があります。

1.コンデンサとインダクタンスのインピーダンス
角周波数\( \ \omega \ \)としたとき，各インピーダンス\( \ \dot Z \ \)は以下の通りとなる。
①コンデンサ
\[
\begin{eqnarray}
\dot Z&=&\frac {1}{\mathrm {j}\omega C}　\\[ 5pt ] \end{eqnarray}
\] ②インダクタンス
\[
\begin{eqnarray}
\dot Z&=&\mathrm {j}\omega L　\\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)解答：ト
抵抗\( \ r \ \)とインダクタンス\( \ L \ \)の直列インピーダンスにかかる電圧は\( \ \dot E \ \)であるから，抵抗\( \ r \ \)に流れる電流\( \ \dot I \ \)は，
\[
\begin{eqnarray}
\dot I&=&\frac {1}{r+\mathrm {j}\omega L}\dot E　\\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：イ
インダクタンス\( \ L \ \)にかかる電圧\( \ {\dot V}_{\mathrm{L}} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{L} &=& \mathrm {j}\omega L \dot I 　\\[ 5pt ] &=& \mathrm {j}\omega L \frac {1}{r+\mathrm {j}\omega L}\dot E 　\\[ 5pt ] &=& \frac {\mathrm {j}\omega L}{r+\mathrm {j}\omega L}\dot E　\\[ 5pt ] \end{eqnarray}
\] となる。

(3)解答：チ
静電容量\( \ C \ \)のコンデンサの両端の電圧\( \ {\dot V}_{\mathrm{C}} \ \)は，\( \ R \ \)と\( \ C \ \)の分圧であるから，
\[
\begin{eqnarray}
{\dot V}_{\mathrm{C}} &=& \frac {\displaystyle \frac {1}{\mathrm {j}\omega C}}{\displaystyle R+\frac {1}{\mathrm {j}\omega C}}\dot E 　\\[ 5pt ] &=& \frac {1}{1+\mathrm {j}\omega CR}\dot E \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヲ
抵抗\( \ r \ \)にかかる電圧を\( \ {\dot V}_{\mathrm{r}} \ \)とするとき，
\[
\begin{eqnarray}
{\dot V}_{\mathrm{r}} &=& r \dot I \\[ 5pt ] &=& r \frac {1}{r+\mathrm {j}\omega L}\dot E \\[ 5pt ] &=& \frac {r}{r+\mathrm {j}\omega L}\dot E \\[ 5pt ] \end{eqnarray}
\] であるから，\( \ {\dot V}_{\mathrm{C}}={\dot V}_{\mathrm{r}} \ \)となるとき，
\[
\begin{eqnarray}
\frac {1}{1+\mathrm {j}\omega CR}\dot E &=& \frac {r}{r+\mathrm {j}\omega L}\dot E \\[ 5pt ] \frac {1}{1+\mathrm {j}\omega CR} &=& \frac {r}{r+\mathrm {j}\omega L} \\[ 5pt ] r+\mathrm {j}\omega CRr &=& r+\mathrm {j}\omega L \\[ 5pt ] \mathrm {j}\omega CRr &=& \mathrm {j}\omega L \\[ 5pt ] CRr &=& L \\[ 5pt ] Rr &=& \frac {L}{C} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：カ
\( \ \displaystyle {\dot V}_{\mathrm{C}}=\frac {1}{1+\mathrm {j}\omega CR}\dot E \ \)，\( \ \displaystyle {\dot V}_{\mathrm{L}}=\frac {\mathrm {j}\omega L}{r+\mathrm {j}\omega L}\dot E \ \)であり，
\[
\begin{eqnarray}
{\dot V}_{\mathrm{L}}&=&\frac {\mathrm {j}\omega L}{r+\mathrm {j}\omega L}\dot E \\[ 5pt ] &=&\frac {\mathrm {j}\omega CRr}{r+\mathrm {j}\omega CRr}\dot E \\[ 5pt ] &=&\frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}\dot E \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
\frac {{\dot V}_{\mathrm{C}}}{{\dot V}_{\mathrm{L}}} &=& \frac {\displaystyle \frac {1}{1+\mathrm {j}\omega CR}\dot E}{\displaystyle \frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}\dot E}\\[ 5pt ] &=& \frac {1}{\mathrm {j}\omega CR} \\[ 5pt ] &=& -\mathrm {j}\frac {1}{\omega CR} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ {\dot V}_{\mathrm{C}} \ \)の位相は\( \ {\dot V}_{\mathrm{L}} \ \)に対して，\( \ 90° \ \)遅れていることとなる。