《理論》〈電子理論〉[H28:問7]電子回路のエミッタフォロワに関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，増幅回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

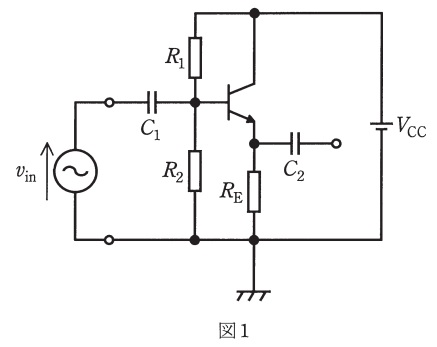
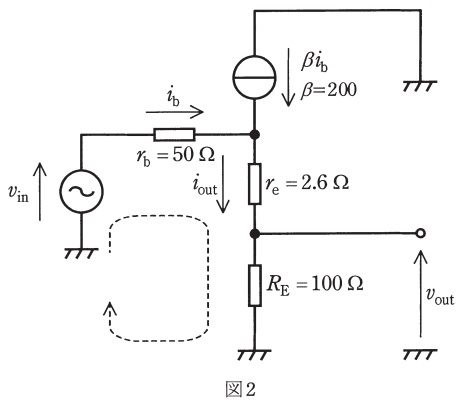
図1の回路は\( \ \fbox {　 （１） 　} \ \)接地増幅回路又はエミッタフォロワと呼ばれる回路であり，その小信号等価回路(交流等価回路)は図2で与えられる。
図2において，電流\( \ i_{\mathrm{b}} \ \)が図に示す向きに流れるとき，\( \ r_{\mathrm{e}} \ \)及び\( \ R_{\mathrm{E}} \ \)に流れる電流\( \ i_{\mathrm{out}} \ \)は\( \ \fbox {　 （２） 　} \ \)となる。よって，出力電圧\( \ v_{\mathrm{out}} \ \)は，
\[
v_{\mathrm{out}}=\fbox {　 （２） 　}\times R_{\mathrm{E}}　　・・・・・・・・・・・・・・①
\] と表される。一方，図2中の点線で表す経路にキルヒホッフの電圧則を適用することで，入力電圧\( \ v_{\mathrm{in}} \ \)を，
\[
v_{\mathrm{in}}=\fbox {　 （３） 　}　・・・・・・・・・・・・・・・・・・②
\] と表すことができる。図1の回路の電圧利得\( \ \displaystyle \frac {v_{\mathrm{out}}}{v_{\mathrm{in}}} \ \)は①式及び②式を用いて，\( \ \displaystyle \frac {v_{\mathrm{out}}}{v_{\mathrm{in}}}= \ \fbox {　 （４） 　} \ \)と導かれる。この結果に図2中の数値を代入し，電圧利得\( \ \displaystyle \frac {v_{\mathrm{out}}}{v_{\mathrm{in}}} \ \)を求めることで，エミッタフォロワは\( \ \fbox {　 （５） 　} \ \)ことが分かる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　エミッタ　　　&（ロ）&　ベース　　　&（ハ）&　コレクタ \\[ 5pt ] &（ニ）&　r_{\mathrm{b}}i_{\mathrm{b}}+\left( 1+\beta \right) r_{\mathrm{e}}i_{\mathrm{b}}　　　&（ホ）&　\frac {-\beta R_{\mathrm{E}}}{r_{\mathrm{b}}+\left( 1+\beta \right) r_{\mathrm{e}}}　　　&（ヘ）&　r_{\mathrm{b}}i_{\mathrm{b}}+\beta \left( r_{\mathrm{e}}+ R_{\mathrm{E}}\right) i_{\mathrm{b}} \\[ 5pt ] &（ト）&　\frac {-\left( 1+\beta \right) R_{\mathrm{E}}}{r_{\mathrm{b}}+\beta \left( r_{\mathrm{e}}+R_{\mathrm{E}} \right) }　　　&（チ）&　i_{\mathrm{b}} 　　　&（リ）&　\left( 1+\beta \right) i_{\mathrm{b}} \\[ 5pt ] &（ヌ）&　\beta i_{\mathrm{b}}　　　&（ル）&　\frac {\left( 1+\beta \right) R_{\mathrm{E}}}{r_{\mathrm{b}}+\left( 1+\beta \right) \left( r_{\mathrm{e}}+R_{\mathrm{E}} \right) }　　　　&（ヲ）&　r_{\mathrm{b}}i_{\mathrm{b}}+\left( 1+\beta \right) \left( r_{\mathrm{e}}+ R_{\mathrm{E}}\right) i_{\mathrm{b}}
\end{eqnarray}
\]\[
\begin{eqnarray}
&（ワ）&　非反転増幅回路であり，ほぼ \ 1 \ 倍の電圧利得を有する \\[ 5pt ] &（カ）&　反転増幅回路であり，大きな電圧利得を有する \\[ 5pt ] &（ヨ）&　反転増幅回路であり，ほぼ \ -1 \ 倍の電圧利得を有する
\end{eqnarray}
\]

【ワンポイント解説】

電子回路は回路が違っても基本的な解き方は同じです。毎年のように出題されるので，確実に得点源となるようにしましょう。

【解答】

(1)解答：ハ
小信号等価回路において，直流電圧源\( \ V_{\mathrm{CC}} \ \)は短絡すれば良いので，図1の回路はコレクタが接地された回路となる。

(2)解答：リ
\( \ r_{\mathrm{e}} \ \)に流れる電流は，\( \ r_{\mathrm{b}} \ \)に流れる電流\( \ i_{\mathrm{b}} \ \)と電流源側から流れてくる電流\( \ \beta i_{\mathrm{b}} \ \)との合計になるので，
\[
\begin{eqnarray}
i_{\mathrm{out}}&=&i_{\mathrm{b}}+\beta i_{\mathrm{b}} \\[ 5pt ] &=&\left( 1+\beta \right) i_{\mathrm{b}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヲ
図2の閉回路にキルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
v_{\mathrm{in}}&=&r_{\mathrm{b}}i_{\mathrm{b}}+\left( r_{\mathrm{e}}+R_{\mathrm{E}}\right) i_{\mathrm{out}} \\[ 5pt ] &=&r_{\mathrm{b}}i_{\mathrm{b}}+\left( 1+\beta \right) \left( r_{\mathrm{e}}+ R_{\mathrm{E}}\right) i_{\mathrm{b}}
\end{eqnarray}
\] と求められる。

(4)解答：ル
①，②より，
\[
\begin{eqnarray}
\frac {v_{\mathrm{out}}}{v_{\mathrm{in}}}&=&\frac {\left( 1+\beta \right) i_{\mathrm{b}}R_{\mathrm{E}}}{r_{\mathrm{b}}i_{\mathrm{b}}+\left( 1+\beta \right) \left( r_{\mathrm{e}}+ R_{\mathrm{E}}\right) i_{\mathrm{b}}} \\[ 5pt ] &=&\frac {\left( 1+\beta \right) R_{\mathrm{E}}}{r_{\mathrm{b}}+\left( 1+\beta \right) \left( r_{\mathrm{e}}+R_{\mathrm{E}} \right) }
\end{eqnarray}
\] と求められる。

(5)解答：ワ
(4)の解答に各値を代入すると，
\[
\begin{eqnarray}
\frac {v_{\mathrm{out}}}{v_{\mathrm{in}}}&=&\frac {\left( 1+200 \right) \times 100}{50+\left( 1+200 \right) \left( 2.6+100 \right) } \\[ 5pt ] &=&\frac {20100}{20672.6} \\[ 5pt ] &≒&0.97
\end{eqnarray}
\] となる。よって，電圧利得はほぼ\( \ 1 \ \)倍であり，非反転増幅回路である。