《理論》〈電気・電子計測〉[H28:問8] 周波数の測定に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，周波数の測定に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

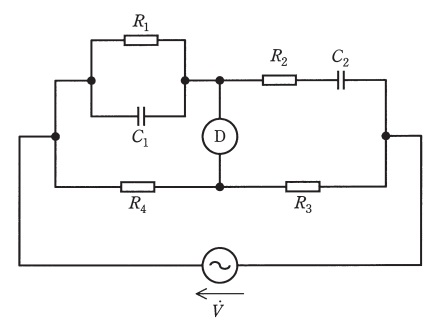
図に示す交流ブリッジ回路において，交流電源の電圧を\( \ \dot V \ \)，その角周波数を\( \ \omega \ \) ( \( \ \omega =2\pi f \ \)，\( \ f \ \)は周波数)，\( \ R_{1}～R_{4} \ \)を抵抗，\( \ C_{1} \ \)及び\( \ C_{2} \ \)を静電容量，Ⓓを検出器とする。
いま，検出器の指示が零となりブリッジが平衡したとすると，以下の関係が成立する。
\[
\begin{eqnarray}
R_{3}\left( \frac {R_{1}}{ \ \fbox {　 （１） 　}} \ \right) &=&R_{4}\left( \frac {1+\mathrm {j}\omega C_{2}R_{2}}{\mathrm {j}\omega C_{2}}\right)　・・・・・・・・・・・① \\[ 5pt ] \end{eqnarray}
\] ①式の虚数部より\( \ C_{1}= \ \fbox {　 （２） 　} \ C_{2} \ \)となる。また，実数部より\( \ \fbox {　 （３） 　} \ =1 \ \)となるから，交流電源の周波数\( \ f \ \)は，\( \ \displaystyle \frac {1}{2\pi \sqrt { \ \fbox {　 （４） 　} \ }}\)で表される。
このような交流ブリッジは一般に\( \ \fbox {　 （５） 　} \ \)ブリッジと呼ばれ，ブリッジの平衡条件に周波数が関係するため，周波数の測定に利用することができる。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　1-\mathrm {j}\omega C_{1}R_{1}　　　&（ロ）&　ケルビンダブル　　　&（ハ）&　1+\mathrm {j}\omega C_{1}R_{1} \\[ 5pt ] &（ニ）&　C_{1}C_{2}R_{1}R_{2}　　　&（ホ）&　C_{1}C_{2}R_{1}R_{4}　　　&（ヘ）&　\omega ^{2}C_{1}C_{2}R_{1}R_{4} \\[ 5pt ] &（ト）&　ホイートストン　　　&（チ）&　\frac {R_{1}R_{3}}{R_{4}} 　　　&（リ）&　\mathrm {j}\omega C_{1} \\[ 5pt ] &（ヌ）&　ウィーン　　　&（ル）&　C_{1}C_{2}R_{2}R_{4}　　　&（ヲ）&　\frac {R_{1}R_{3}-R_{2}R_{4}}{R_{1}R_{4}}　 \\[ 5pt ] &（ワ）&　\frac {R_{2}R_{4}-R_{1}R_{3}}{R_{2}R_{3}}　　　&（カ）&　\omega ^{2}C_{1}C_{2}R_{2}R_{4}　　　&（ヨ）&　\omega ^{2}C_{1}C_{2}R_{1}R_{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ウィーンブリッジは回路が平衡となった時の周波数を抵抗とコンデンサの値から導出できるものです。ホイートストンブリッジと似ていますが，ホイートストンブリッジは問題図の\( \ C_{1} \ \)と\( \ C_{2} \ \)がないものです。

1.交流ブリッジの平衡条件
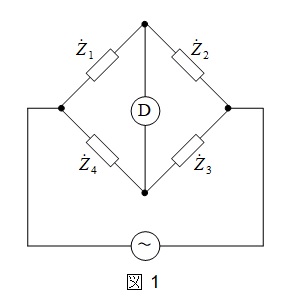
図1の回路において，検流計Ⓓに電流が流れない平衡条件は，
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{4}}&=&\frac {Z_{2}}{Z_{3}} \\[ 5pt ] Z_{1}Z_{3}&=&Z_{2}Z_{4} \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　静電容量測定用ブリッジ回路まとめ

【解答】

(1)解答：ハ
\( \ R_{1} \ \)と\( \ C_{1} \ \)の合成インピーダンスは，
\[
\begin{eqnarray}
\frac {\displaystyle R_{1}\frac {1}{\mathrm {j}\omega C_{1}}}{\displaystyle R_{1}+\frac {1}{\mathrm {j}\omega C_{1}}}&=&\frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}} \\[ 5pt ] \end{eqnarray}
\] であるから，回路の平衡条件は，
\[
\begin{eqnarray}
R_{3}\left( \frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}}\right) &=&R_{4}\left( \frac {1+\mathrm {j}\omega C_{2}R_{2}}{\mathrm {j}\omega C_{2}}\right) \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ヲ
①を展開して整理すると，
\[
\begin{eqnarray}
R_{3}\left( \frac {R_{1}}{1+\mathrm {j}\omega C_{1}R_{1}}\right) &=&R_{4}\left( \frac {1+\mathrm {j}\omega C_{2}R_{2}}{\mathrm {j}\omega C_{2}}\right) \\[ 5pt ] \mathrm {j}\omega C_{2}R_{1}R_{3}&=&R_{4}\left( 1+\mathrm {j}\omega C_{1}R_{1}\right) \left( 1+\mathrm {j}\omega C_{2}R_{2}\right) \\[ 5pt ] &=&R_{4}\left( 1-\omega ^{2}C_{1}C_{2}R_{1}R_{2}\right) +\mathrm {j}\omega R_{4}\left( C_{1}R_{1}+C_{2}R_{2}\right) \\[ 5pt ] \end{eqnarray}
\] 虚数部の係数比較すると，
\[
\begin{eqnarray}
\omega C_{2}R_{1}R_{3} &=&\omega R_{4}\left( C_{1}R_{1}+C_{2}R_{2}\right) \\[ 5pt ] C_{2}R_{1}R_{3} &=&R_{4}\left( C_{1}R_{1}+C_{2}R_{2}\right) \\[ 5pt ] R_{1}R_{4}C_{1} &=&R_{1}R_{3}C_{2}-R_{2}R_{4}C_{2} \\[ 5pt ] C_{1} &=&\frac {R_{1}R_{3}-R_{2}R_{4}}{R_{1}R_{4}}C_{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヨ
同様に実数部を比較すると，
\[
\begin{eqnarray}
0 &=&1-\omega ^{2}C_{1}C_{2}R_{1}R_{2} \\[ 5pt ] \omega ^{2}C_{1}C_{2}R_{1}R_{2} &=&1 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ニ
(3)解答において\( \ \omega =2\pi f \ \)に注意して整理すると，
\[
\begin{eqnarray}
\omega ^{2} &=&\frac {1}{C_{1}C_{2}R_{1}R_{2}} \\[ 5pt ] \omega &=&\frac {1}{\sqrt {C_{1}C_{2}R_{1}R_{2}}} \\[ 5pt ] 2\pi f &=&\frac {1}{\sqrt {C_{1}C_{2}R_{1}R_{2}}} \\[ 5pt ] f &=&\frac {1}{2\pi\sqrt {C_{1}C_{2}R_{1}R_{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
本回路はウィーンブリッジと呼ばれます。