【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,影像電荷による静電界の解法に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
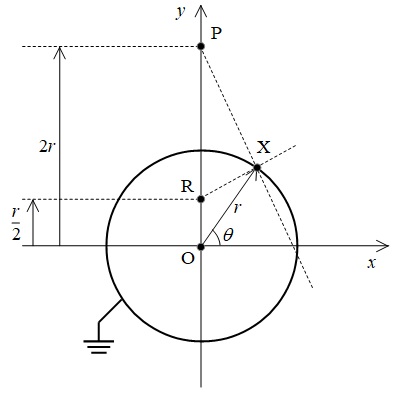
真空中に,原点\( \ \mathrm {O} \ \)を中心とする半径\(r\)の接地された導体球がある。図は原点を通る断面であり,\( \ xy \ \)平面を図のようにとり,以下では対称性により\( \ xy \ \)平面上で考える。このとき\( \ y \ \)軸上の点\( \ \mathrm {P} \ \)の座標を\( \ ( 0,2r ) \ \)とし,そこには電荷量\( \ Q ( > 0 ) \ \)の点電荷が置かれている。なお,真空中の誘電率を\( \ \varepsilon _{0} \ \)とする。
球面上の点\( \ \mathrm {X} \ \)の座標を\( \ ( r\cos \theta ,r\sin \theta ) \ \)とすると,導体球がなくて点\( \ \mathrm {P} \ \)の電荷だけを考えた場合の点\( \ \mathrm {X} \ \)の電位と電界の大きさは,それぞれ\( \ \fbox { (1) } \ \),\( \ \fbox { (2) } \ \)である。
次に,導体球の代わりに,電荷量\( \ -q ( > 0 ) \ \)の影像電荷を\( \ y \ \)軸上の点\( \ \mathrm {R} ( 0,\displaystyle \frac {r}{2} ) \ \)を仮想的に置く。点\( \ \mathrm {X} \ \)の位置が\( \ \displaystyle \theta =\frac {\pi }{2} \ \)のとき,そこの電位が零となる\( \ q \ \)は,\( \ \fbox { (3) } \ \)である。このとき,任意の\( \ \theta \ \)について点\( \ \mathrm {X} \ \)の電位が零となる。
この影像電荷を利用すると,点\( \ \mathrm {P} \ \)の電荷が導体球に誘導された電荷から受ける力の大きさは,\( \ \fbox { (4) } \ \)であると分かる。また,点\( \ \mathrm {X} \ \)の位置が\( \ \displaystyle \theta =0 \ \)のとき,そこにおける電界ベクトル\( \ \boldsymbol E = ( E_{\mathrm {x}},E_{\mathrm {y}} ) \ \)は,\( \ \fbox { (5) } \ \)である。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {Q}{2} &(ロ)& \frac {Q^{2}}{9\pi \varepsilon _{0} r^{2}} &(ハ)& \left( -\frac {3Q}{50\pi \varepsilon _{0} r^{2}},-\frac {3Q}{100\pi \varepsilon _{0} r^{2}} \right) \\[ 5pt ]
&(ニ)& \frac {Q}{4\pi \varepsilon _{0} r^{2}\left( 5-4\sin \theta \right) } &(ホ)& \frac {Q}{4\sqrt {5}\pi \varepsilon _{0} r } &(ヘ)& \frac {Q}{4\pi \varepsilon _{0} r^{2}\left( 5+4\sin \theta \right) } \\[ 5pt ]
&(ト)& \frac {Q^{2}}{18\pi \varepsilon _{0} r^{2}} &(チ)& \left( 0,-\frac {3\sqrt {5}Q}{100\pi \varepsilon _{0} r^{2}} \right) &(リ)& \left( -\frac {3\sqrt {5}Q}{100\pi \varepsilon _{0} r^{2}},0 \right) \\[ 5pt ]
&(ヌ)& 2Q &(ル)& \frac {Q}{4\pi \varepsilon _{0} r\sqrt{ 5-4\sin \theta } } &(ヲ)& \frac {Q}{4\pi \varepsilon _{0} r\sqrt{ 5+4\sin \theta } } \\[ 5pt ]
&(ワ)& \frac {Q}{20\pi \varepsilon _{0} r^{2}} &(カ)& \frac {Q^{2}}{32\pi \varepsilon _{0} r^{2}} &(ヨ)& Q \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
扱う公式は三種でも出題される電磁気の基本公式のみですが,計算がやや複雑な問題となっています。(5)は計算に時間がかかるので,他の問題が終わってから取り組んだ方が時間切れにならないと思われます。
1.クーロンの法則
真空中で距離\( \ r \ \)離れた点電荷\( \ Q_{1} \ \)と\( \ Q_{2} \ \)に加わる力の大きさ\( \ F \ \)は,
\[
\begin{eqnarray}
F&=&\frac {Q_{1}Q_{2}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ Q_{1} \ \)と\( \ Q_{2} \ \)が同符号の時斥力,\( \ Q_{1} \ \)と\( \ Q_{2} \ \)が異符号の時引力が働きます。
2.電界の強さ\( \ E \ \)
真空中で\( \ Q \ \)が作る電界の大きさ\( \ E \ \)は,距離\( \ r \ \)の地点で,
\[
\begin{eqnarray}
E&=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.点電荷の作る電位\( \ V \ \)
真空中で\( \ Q \ \)が作る電位\( \ V \ \)は,電界の強さ\( \ E \ \)より,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r} E \mathrm {d}r \\[ 5pt ]
&=&-\int _{\infty }^{r} \frac {Q}{4\pi \varepsilon _{0}r^{2}} \mathrm {d}r \\[ 5pt ]
&=&-\left[ -\frac {Q}{4\pi \varepsilon _{0}r}\right] _{\infty }^{r} \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ル
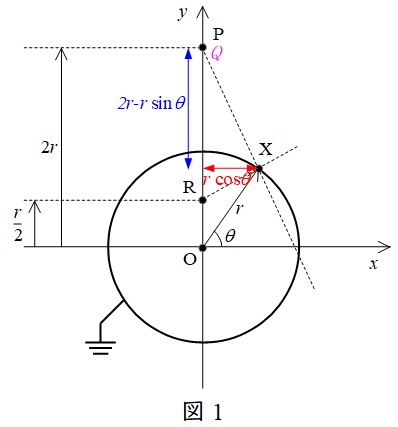
図1の通り各部の長さが求められるので,点\( \ \mathrm {P} \ \)と点\( \ \mathrm {X} \ \)の距離\( \ R \ \)は,三平方の定理より,
\[
\begin{eqnarray}
R&=& \sqrt {\left( r\cos \theta \right) ^{2} +\left( 2r-r\sin \theta \right) ^{2}} \\[ 5pt ]
&=& \sqrt { r ^{2}\cos ^{2}\theta + 4r^{2}-4r^{2}\sin \theta + r^{2}\sin ^{2}\theta } \\[ 5pt ]
&=& r\sqrt { 4-4\sin \theta + \sin ^{2}\theta +\cos ^{2}\theta } \\[ 5pt ]
&=&r\sqrt { 4-4\sin \theta + 1 } \\[ 5pt ]
&=&r\sqrt { 5-4\sin \theta } \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,ワンポイント解説「3.点電荷の作る電位\( \ V \ \)」より,点\( \ \mathrm {X} \ \)の電位\( \ V_{\mathrm {X1}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {X1}}&=& \frac {Q}{4\pi \varepsilon _{0}R} \\[ 5pt ]
&=& \frac {Q}{4\pi \varepsilon _{0}r\sqrt { 5-4\sin \theta }} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
ワンポイント解説「2.電界の強さ\( \ E \ \)」より,点\( \ \mathrm {X} \ \)の電界の強さ\( \ E_{\mathrm {X}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {X}}&=& \frac {Q}{4\pi \varepsilon _{0}R^{2}} \\[ 5pt ]
&=& \frac {Q}{4\pi \varepsilon _{0} r^{2}\left( 5-4\sin \theta \right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:イ
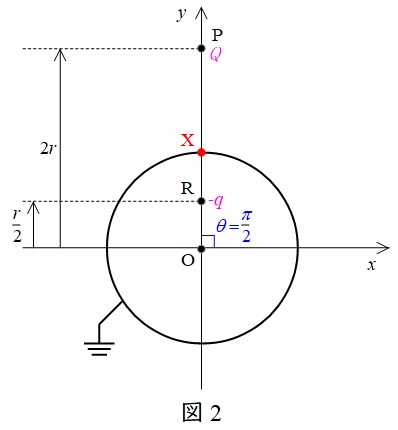
題意に沿って図を描くと図2のようになる。
この時電荷\( \ Q \ \)と電荷\( \ -q \ \)による電位\( \ V_{\mathrm {X2}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {X2}}&=& \frac {Q}{4\pi \varepsilon _{0}r}-\frac {q}{4\pi \varepsilon _{0}\frac {r}{2}} \\[ 5pt ]
&=& \frac {Q}{4\pi \varepsilon _{0}r}-\frac {2q}{4\pi \varepsilon _{0}r} \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より,\( \ V_{\mathrm {X2}}=0 \ \)であるから,
\[
\begin{eqnarray}
\frac {Q}{4\pi \varepsilon _{0}r}-\frac {2q}{4\pi \varepsilon _{0}r}&=& 0 \\[ 5pt ]
\frac {Q}{4\pi \varepsilon _{0}r}&=&\frac {2q}{4\pi \varepsilon _{0}r} \\[ 5pt ]
Q&=&2q \\[ 5pt ]
q&=&\frac {Q}{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ト
点\( \ \mathrm {P} \ \)の電荷が導体球に誘導された電荷から受ける力の大きさは,影像電荷と点\( \ \mathrm {P} \ \)の電荷に働く力の大きさと等しいので,ワンポイント解説「1.クーロンの法則」より,
\[
\begin{eqnarray}
F&=&\frac {Qq}{4\pi \varepsilon _{0}\left( \frac {3}{2}r\right) ^{2}} \\[ 5pt ]
&=&\frac {Q\frac {Q}{2}}{4\pi \varepsilon _{0}\left( \frac {3}{2}r\right) ^{2}} \\[ 5pt ]
&=&\frac {Q^{2}}{18\pi \varepsilon _{0} r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
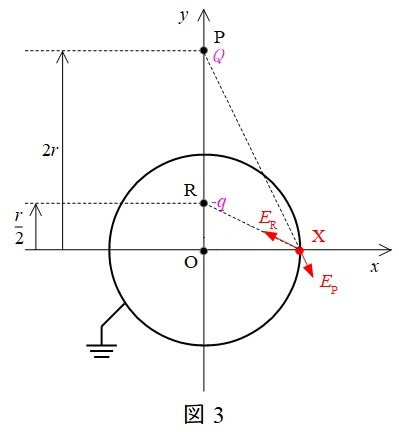
(5)解答:リ
題意に沿って図を描くと図3のようになる。図3において,点\( \ \mathrm {P} \ \)と点\( \ \mathrm {X} \ \)の距離\( \ r_{\mathrm {PX}} \ \)と点\( \ \mathrm {R} \ \)と点\( \ \mathrm {X} \ \)の距離\( \ r_{\mathrm {RX}} \ \)は,
\[
\begin{eqnarray}
r_{\mathrm {PX}}&=&\sqrt {r^{2}+\left( 2r\right) ^{2}} \\[ 5pt ]
&=&\sqrt {5}r \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
r_{\mathrm {RX}}&=&\sqrt {r^{2}+\left( \frac {r}{2}\right) ^{2}} \\[ 5pt ]
&=&\frac {\sqrt {5}}{2}r \\[ 5pt ]
\end{eqnarray}
\]
であるからそれぞれの電荷が作る電界の強さ\( \ E_{\mathrm {P}} \ \)と\( \ E_{\mathrm {R}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {P}}&=&\frac {Q}{4\pi \varepsilon _{0}{r_{\mathrm {PX}}}^{2}} \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon _{0}\left( \sqrt {5}r\right) ^{2}} \\[ 5pt ]
&=&\frac {Q}{20\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
E_{\mathrm {R}}&=&\frac {q}{4\pi \varepsilon _{0}{r_{\mathrm {RX}}}^{2}} \\[ 5pt ]
&=&\frac {\frac {Q}{2}}{4\pi \varepsilon _{0}\left( \frac {\sqrt {5}}{2}r\right) ^{2}} \\[ 5pt ]
&=&\frac {Q}{10\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。これより,合成電界の\( \ x \ \)成分\( \ E_{\mathrm {x}} \ \)と\( \ y \ \)成分\( \ E_{\mathrm {y}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&E_{\mathrm {P}}\cdot \frac {r}{\sqrt {5}r} – E_{\mathrm {R}}\cdot \frac {r}{\frac {\sqrt {5}}{2}r}\\[ 5pt ]
&=&\frac {Q}{20\pi \varepsilon _{0}r^{2}}\cdot \frac {1}{\sqrt {5}} – \frac {Q}{10\pi \varepsilon _{0}r^{2}}\cdot \frac {2}{\sqrt {5}}\\[ 5pt ]
&=&-\frac {3Q}{20\sqrt {5} \pi \varepsilon _{0}r^{2}} \\[ 5pt ]
&=&-\frac {3\sqrt {5} Q}{100 \pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
E_{\mathrm {y}}&=&E_{\mathrm {P}}\cdot \frac {2r}{\sqrt {5}r} – E_{\mathrm {R}}\cdot \frac {\frac {r}{2}}{\frac {\sqrt {5}}{2}r}\\[ 5pt ]
&=&\frac {Q}{20\pi \varepsilon _{0}r^{2}}\cdot \frac {2}{\sqrt {5}} – \frac {Q}{10\pi \varepsilon _{0}r^{2}}\cdot \frac {1}{\sqrt {5}}\\[ 5pt ]
&=&\frac {Q}{10\sqrt {5}\pi \varepsilon _{0}r^{2}}-\frac {Q}{10\sqrt {5}\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは