《理論》〈電気回路〉[H30:問3]LC並列回路の過渡現象に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，回路の過渡現象に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選べ。

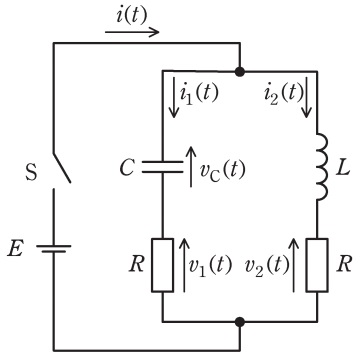
図に示す，コンデンサ，抵抗，コイル，直流電圧源からなる回路を考える。時刻\( \ t＜0 \ \)でスイッチ\( \ \mathrm {S} \ \)は開いており，各素子の電圧，電流は零とする。

\( t=0 \ \)でスイッチ\( \ \mathrm {S} \ \)を閉じると，\( \ t≧0 \ \)でコンデンサの電圧は，\( \ v_{\mathrm {C}}(t)=E\times \left( \fbox {　 （１） 　}\right) =E-v_{1}(t) \)，コイルの電流は\(\displaystyle \ i_{2}(t)=\frac {E}{R}\times \left( \fbox {　 （２） 　}\right) \)となる。これらより，\( \ t≧0 \ \)で直流電圧源\( \ E \ \)を流れる電流は，
\[
\begin{eqnarray}
i(t)&=&i_{1}(t)+i_{2}(t)=\frac {v_{1}(t)}{R}+i_{2}(t)=\frac {E}{R}\times \left( \fbox {　 （３） 　}\right) \\[ 5pt ] \end{eqnarray}
\] となる。特に\( \ \displaystyle \frac {1}{CR}=\frac {R}{L} \ \)のときは\(\fbox {　 （３） 　}\)は一定であり，\( \ t≧0 \ \)で，
\[
\begin{eqnarray}
i_{1}(t)+i_{2}(t)&=&\frac {E}{R}(一定値)　　・・・・・・・・・・・・・・・① \\[ 5pt ] \end{eqnarray}
\] が成立する。

次に，\( \ \displaystyle \frac {1}{CR}=\frac {R}{L} \ \)のときに\( \ i_{1}(t)=i_{2}(t) \ \)となる時刻\( \ t \ \)を\( \ T (＞0) \ \)で表すと，\(\displaystyle \ i_{1}(T)=\frac {E}{R}\times \fbox {　 （４） 　}\)及び①式より\(\displaystyle \ i_{1}(T)=i_{2}(T)=\frac {E}{2R} \ \)であるから，\(\displaystyle \fbox {　 （４） 　}=\frac {1}{2} \ \)となる。両辺の対数をとると，\(T=\fbox {　 （５） 　}\)が求められる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　1-\mathrm {e}^{-\frac {1}{CR}t}　　　&（ロ）&　1+\mathrm {e}^{-\frac {1}{CR}t}　　　&（ハ）&　2-\mathrm {e}^{-\left( \frac {1}{CR}-\frac {R}{L}\right) t} \\[ 5pt ] &（ニ）&　\mathrm {e}^{-\frac {1}{CR}T}　　　&（ホ）&　2-\mathrm {e}^{\left( \frac {1}{CR}-\frac {R}{L}\right) t}　　　&（ヘ）&　1+\mathrm {e}^{-\frac {R}{L}t} \\[ 5pt ] &（ト）&　\mathrm {e}^{-\frac {1}{2CR}T}　　　&（チ）&　\mathrm {e}^{-\frac {R}{L}t}-2　　　　&（リ）&　\ln CR \\[ 5pt ] &（ヌ）&　1-\mathrm {e}^{-\frac {R}{L}t}　　　&（ル）&　1+\mathrm {e}^{-\frac {1}{CR}t}-\mathrm {e}^{-\frac {R}{L}t}　　　&（ヲ）&　CR \ln 2 \\[ 5pt ] &（ワ）&　\mathrm {e}^{-\frac {1}{CR}t}-2　　　&（カ）&　2\ln CR　　　&（ヨ）&　\mathrm {e}^{-\frac {2}{CR}T} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電験二種ならではの過渡現象に関する問題です。最初はとっつきにくいですが，慣れてしまえばパターンが決まっているので，確実に得点源になります。本問の場合はコイルとコンデンサの両方の導出を練習できますので，練習問題としては非常に良い問題と言えます。

1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \)とし，抵抗\( \ R \ \)の電圧\( \ V_{\mathrm{R}} \ \)，リアクトル\( \ L \ \)の電圧\( \ V_{\mathrm{L}} \ \)，コンデンサ\( \ C \ \)の電圧\( \ V_{\mathrm{C}} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ] V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ] V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となり，電荷\( \ q \ \)との間に\( \ \displaystyle i=\frac {\mathrm {d}q}{\mathrm {d}t} \ \)の関係があるので，
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& R\frac {\mathrm {d}q}{\mathrm {d}t} \\[ 5pt ] V_{\mathrm{L}} &=& L\frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}} \\[ 5pt ] V_{\mathrm{C}} &=& \frac {q}{C}
\end{eqnarray}
\] となります。

2.過渡現象における定常解と過渡解
ⅰ．定常解を\( \ i_{\mathrm {s}} \ \)，過渡解を\( \ i_{\mathrm {t}} \ \)とすると，電流値\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ．定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ．過渡解はスイッチを入れた直後の解すなわち\( \ L \ \)開放(\( \ E=0 \ \)と同義)の時の解です。

3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x}　\\[ 5pt ] \end{eqnarray}
\] ②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right)　\\[ 5pt ] \end{eqnarray}
\] となり，
\[
\begin{eqnarray}
\ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ] \end{eqnarray}
\] となった場合，両辺とも対数を外すと，
\[
\begin{eqnarray}
x&=&A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right) \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　LC並列回路の過渡現象（直流回路）

【解答】

(1)解答：イ
電源\( \ E \ \)とコンデンサ\( \ C \ \)，抵抗\( \ R \ \)が作る閉回路の回路方程式は，\(t\)秒後にコンデンサに蓄えられる電荷を\(q_{1}(t)\)と置くと，
\[
\begin{eqnarray}
v_{1}(t) +v_{\mathrm {C}}(t) &=&E \\[ 5pt ] Ri_{1}(t) +\frac {1}{C}\int i_{1}(t) \mathrm {d}t &=&E \\[ 5pt ] R\frac {\mathrm {d}q_{1}}{\mathrm {d}t} +\frac {q_{1}}{C} &=&E \\[ 5pt ] \end{eqnarray}
\] となる。

ワンポイント解説「2.過渡現象における定常解と過渡解」の通り，定常解を\(q_{\mathrm {1s}}\)，過渡解を\(q_{\mathrm {1t}}\)と置くと，\(\displaystyle \frac {dq_{\mathrm {1s}}}{dt}=0\)であるから，
\[
\begin{eqnarray}
\frac {q_{\mathrm {1s}}}{C} &=&E \\[ 5pt ] q_{\mathrm {1s}} &=&CE \\[ 5pt ] \end{eqnarray}
\] と求められる。一方，過渡解は\(E=0\)とすると，
\[
\begin{eqnarray}
R\frac {\mathrm {d}q_{\mathrm {1t}}}{\mathrm {d}t} +\frac {q_{\mathrm {1t}}}{C} &=&0 \\[ 5pt ] R\frac {\mathrm {d}q_{\mathrm {1t}}}{\mathrm {d}t} &=&-\frac {q_{\mathrm {1t}}}{C} \\[ 5pt ] \frac {1}{q_{\mathrm {1t}}}\mathrm {d}q_{\mathrm {1t}} &=&-\frac {1}{CR}\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となり，両辺積分をとると，
\[
\begin{eqnarray}
\int \frac {1}{q_{\mathrm {1t}}}\mathrm {d}q_{\mathrm {1t}} &=&\int \left( -\frac {1}{CR}\right) \mathrm {d}t \\[ 5pt ] \ln q_{\mathrm {1t}} &=& -\frac {1}{CR}t+C^{\prime }\left( C^{\prime }は積分定数\right) \\[ 5pt ] q_{\mathrm {1t}} &=& A\mathrm {e}^{-\frac {1}{CR}t}\left( Aは積分定数\right) \\[ 5pt ] \end{eqnarray}
\] と求められるので，一般解は，
\[
\begin{eqnarray}
q_{1}(t) &=&q_{\mathrm {1s}}+q_{\mathrm {1t}} \\[ 5pt ] &=& CE+A\mathrm {e}^{-\frac {1}{CR}t} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\(q_{1}(0)=0\)であるので，\(A=-CE\)となり，
\[
\begin{eqnarray}
q_{1}(t) &=& CE\left( 1-\mathrm {e}^{-\frac {1}{CR}t}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，コンデンサの電圧\( \ v_{\mathrm {C}}(t) \ \)は，
\[
\begin{eqnarray}
v_{\mathrm {C}}(t) &=& \frac {q_{1}(t)}{C} \\[ 5pt ] &=&E\left( 1-\mathrm {e}^{-\frac {1}{CR}t}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヌ
電源\( \ E \ \)とコイル\( \ L \ \)，抵抗\( \ R \ \)が作る閉回路の回路方程式は，\(t\)秒後にコイルに流れる電流を\(i_{2}(t)\)と置くと，
\[
\begin{eqnarray}
v_{2}(t) +L\frac {\mathrm {d}i_{2}}{\mathrm {d}t} &=&E \\[ 5pt ] Ri_{2}(t) +L\frac {\mathrm {d}i_{2}}{\mathrm {d}t} &=&E \\[ 5pt ] \end{eqnarray}
\] となる。

ワンポイント解説「2.過渡現象における定常解と過渡解」の通り，定常解を\(i_{\mathrm {2s}}\)，過渡解を\(i_{\mathrm {2t}}\)と置くと，\(\displaystyle \frac {\mathrm {d}i_{\mathrm {2s}}}{\mathrm {d}t}=0\)であるから，
\[
\begin{eqnarray}
Ri_{\mathrm {2s}} &=&E \\[ 5pt ] i_{\mathrm {2s}} &=&\frac {E}{R} \\[ 5pt ] \end{eqnarray}
\] と求められる。一方，過渡解は\(E=0\)とすると，
\[
\begin{eqnarray}
Ri_{\mathrm {2t}} +L\frac {\mathrm {d}i_{\mathrm {2t}}}{\mathrm {d}t} &=&0 \\[ 5pt ] L\frac {\mathrm {d}i_{\mathrm {2t}}}{\mathrm {d}t} &=&-Ri_{\mathrm {2t}} \\[ 5pt ] \frac {1}{i_{\mathrm {2t}}}\mathrm {d}i_{\mathrm {2t}} &=&-\frac {R}{L}\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となり，両辺積分をとると，
\[
\begin{eqnarray}
\int \frac {1}{i_{\mathrm {2t}}}\mathrm {d}i_{\mathrm {2t}} &=&\int -\frac {R}{L}\mathrm {d}t \\[ 5pt ] \ln i_{\mathrm {2t}} &=& -\frac {R}{L}t+C^{\prime }\left( C^{\prime }は積分定数\right) \\[ 5pt ] i_{\mathrm {2t}} &=& A\mathrm {e}^{-\frac {R}{L}t}\left( Aは積分定数\right) \\[ 5pt ] \end{eqnarray}
\] と求められるので，一般解は，
\[
\begin{eqnarray}
i_{2}(t) &=&i_{\mathrm {2s}}+i_{\mathrm {2t}} \\[ 5pt ] &=& \frac {E}{R}+A\mathrm {e}^{-\frac {R}{L}t} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\(i_{2}(0)=0\)であるので，\(\displaystyle A=-\frac {E}{R}\)となり，
\[
\begin{eqnarray}
i_{2}(t) &=& \frac {E}{R}\left( 1-\mathrm {e}^{-\frac {R}{L}t}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
コンデンサ側の抵抗の電圧\(v_{1}(t)\)は，
\[
\begin{eqnarray}
v_{1}(t) &=& E-v_{\mathrm {C}}(t) \\[ 5pt ] &=& E-E\left( 1-\mathrm {e}^{-\frac {1}{CR}t}\right) \\[ 5pt ] &=& E\mathrm {e}^{-\frac {1}{CR}t} \\[ 5pt ] \end{eqnarray}
\] であるから，直流電圧源に流れる電流\( \ i(t) \ \)は，
\[
\begin{eqnarray}
i(t) &=& i_{1}(t)+i_{2}(t) \\[ 5pt ] &=& \frac {v_{1}(t)}{R}+i_{2}(t) \\[ 5pt ] &=& \frac {E}{R}\mathrm {e}^{-\frac {1}{CR}t}+\frac {E}{R}\left( 1-\mathrm {e}^{-\frac {R}{L}t}\right) \\[ 5pt ] &=& \frac {E}{R}\left( 1+\mathrm {e}^{-\frac {1}{CR}t}-\mathrm {e}^{-\frac {R}{L}t}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ニ
(3)より，
\[
\begin{eqnarray}
i_{1}(T) &=& \frac {v_{1}(T)}{R} \\[ 5pt ] &=& \frac {E}{R}\mathrm {e}^{-\frac {1}{CR}T} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
題意より，
\[
\begin{eqnarray}
i_{1}(T) &=& \frac {E}{2R} \\[ 5pt ] \frac {E}{R}\mathrm {e}^{-\frac {1}{CR}T}&=& \frac {E}{2R} \\[ 5pt ] \mathrm {e}^{-\frac {1}{CR}T}&=& \frac {1}{2} \\[ 5pt ] \end{eqnarray}
\] となり，両辺の対数を取ると，
\[
\begin{eqnarray}
-\frac {1}{CR}T&=& \ln \frac {1}{2} \\[ 5pt ] -\frac {1}{CR}T&=& -\ln 2 \\[ 5pt ] \frac {1}{CR}T&=& \ln 2 \\[ 5pt ] T&=& CR\ln 2 \\[ 5pt ] \end{eqnarray}
\] と求められる。