電験二種過去問解説・理論問5（令和元年度）

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，電流が作る磁界に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

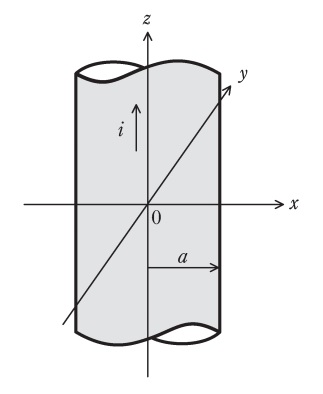
$ \ x \ $，$ \ y \ $，$ \ z \ $軸の直交座標系で表される真空中に，図のように$ \ z \ $軸を中心軸とした半径$ \ a \ $の無限長円柱導体が存在している。導体中には$ \ z \ $軸の正の方向に電流が流れており，電流密度$ \ i\left( ＞0\right) \ $は場所によらず一定とする。なお，導体の透磁率は真空と同じ$ \ \mu _{0} \ $とする。

$ \ z \ $軸を中心とした半径$ \ r=\sqrt {x^{2}+y^{2}} \ $の円断面中を流れる電流は，導体内部$ \ \left( r≦a\right) \ $では$ \ \fbox {　（１）　} \ $となるので，アンペアの周回積分の法則を用いて$ \ z \ $軸から距離$ \ r \ $の地点における磁束密度の大きさを求めることができる。導体内部$ \ \left( r≦a\right) \ $の磁束密度の大きさ$ \ B_{\mathrm {in}} \ $は，
\[
\begin{eqnarray}
B_{\mathrm {in}} &=& \ \fbox {　（２）　} \ \\[ 5pt ] \end{eqnarray}
\] 導体外部の真空中$ \ \left( r＞a\right) \ $の磁束密度の大きさ$ \ B_{\mathrm {out}} \ $は，
\[
\begin{eqnarray}
B_{\mathrm {out}} &=& \ \fbox {　（３）　} \ \\[ 5pt ] \end{eqnarray}
\] となるので，磁束密度の大きさは$ \ r=a \ $において，最大値
\[
\begin{eqnarray}
B_{\mathrm {max}} &=& \ \fbox {　（４）　} \ \\[ 5pt ] \end{eqnarray}
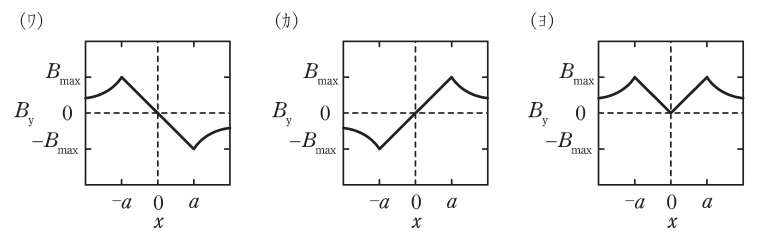
\] をとる。磁界は電流を取り巻くようにできることを考慮すると，磁束密度の$ \ y \ $方向成分$ \ B_{\mathrm {y}} \ $の$ \ x \ $軸に沿った分布の概形は$ \ \fbox {　（５）　} \ $のようになる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\mu _{0}ri}{2}　　　&（ロ）&　\frac {\mu _{0}r^{3}i}{2a}　　　&（ハ）&　\frac {\mu _{0}i}{2a} \\[ 5pt ] &（ニ）&　\frac {\mu _{0}a^{2}i}{2r}　　　&（ホ）&　2\pi ri　　　&（ヘ）&　\frac {\mu _{0}i}{2r} \\[ 5pt ] &（ト）&　\pi r^{2}i　　　&（チ）&　\frac {\mu _{0}ri}{2a^{2}}　　　　&（リ）&　\frac {\pi r^{3}i}{4} \\[ 5pt ] &（ヌ）&　\frac {\mu _{0}ai}{2}　　　&（ル）&　\frac {\mu _{0}r^{2}i}{2}　　　&（ヲ）&　\frac {\mu _{0}a^{2}i}{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

導体内部における電流密度の扱いが最大のポイントとなる問題です。電界でも同様な問題が出題されることがありますが，解き方としては同じです。

1.アンペールの周回積分の法則
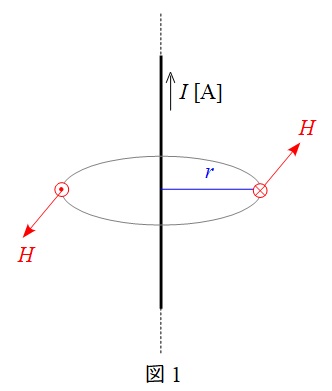
図1のように無限長直線電流$ \ I \ $が流れているとき，電線から距離$ \ r \ $の位置での磁界の強さ$ \ H \ $は，
\[
\begin{eqnarray}
H&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

2.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係
透磁率が$ \ \mu \ $の時，磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係は，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ト
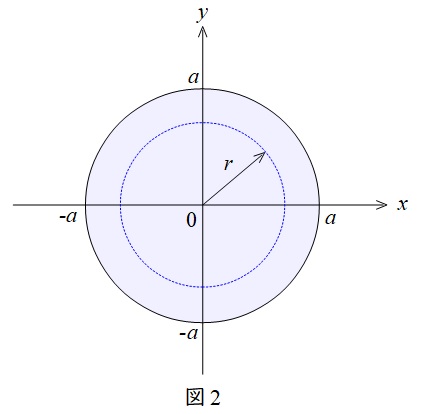
導体内部$ \ \left( r≦a\right) \ $で円断面中を流れる電流$ \ I \ $は図2の通り，半径$ \ r \ $の内部の電流であるから，
\[
\begin{eqnarray}
I&=&\pi r^{2} i \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：イ
ワンポイント解説「1.アンペールの周回積分の法則」より，$ \ z \ $軸から距離$ \ r \ $$ \ \left( r≦a\right) \ $の地点における磁界の大きさ$ \ H_{\mathrm {in}} \ $は，
\[
\begin{eqnarray}
H_{\mathrm {in}}&=&\frac {I}{2\pi r} \\[ 5pt ] &=&\frac {\pi r^{2} i}{2\pi r} \\[ 5pt ] &=&\frac {ri}{2} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「2.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係」より，磁束密度の大きさ$ \ B_{\mathrm {in}} \ $は，
\[
\begin{eqnarray}
B_{\mathrm {in}}&=&\mu _{0}H_{\mathrm {in}} \\[ 5pt ] &=&\frac {\mu _{0}ri}{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ニ
導体外部$ \ \left( r＞a\right) \ $で円断面中を流れる電流$ \ I \ $は，半径$ \ a \ $の電流であるから，
\[
\begin{eqnarray}
I&=&\pi a^{2} i \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「1.アンペールの周回積分の法則」より，$ \ z \ $軸から距離$ \ r \ $$ \ \left( r＞a\right) \ $の地点における磁界の大きさ$ \ H_{\mathrm {out}} \ $は，
\[
\begin{eqnarray}
H_{\mathrm {out}}&=&\frac {I}{2\pi r} \\[ 5pt ] &=&\frac {\pi a^{2} i}{2\pi r} \\[ 5pt ] &=&\frac {a^{2}i}{2r} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「2.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係」より，磁束密度の大きさ$ \ B_{\mathrm {out}} \ $は，
\[
\begin{eqnarray}
B_{\mathrm {out}}&=&\mu _{0}H_{\mathrm {out}} \\[ 5pt ] &=&\frac {\mu _{0}a^{2}i}{2r} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヌ
磁束密度が最大となる$ \ B_{\mathrm {max}} \ $は$ \ r=a \ $の時であるから，
\[
\begin{eqnarray}
B_{\mathrm {max}}&=&\frac {\mu _{0}a^{2}i}{2a} \\[ 5pt ] &=&\frac {\mu _{0}ai}{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：カ
(2)の通り，$ \ r≦a \ $において，磁束密度の大きさ$ \ B_{\mathrm {in}} \ $は$ \ r \ $に比例し，(3)の通り，$ \ r＞a \ $において，磁束密度の大きさ$ \ B_{\mathrm {out}} \ $は$ \ r \ $に反比例する。
また，ワンポイント解説「1.アンペールの周回積分の法則」図1の通り，$ \ r＜0 \ $の時$ \ x \ $軸上の磁束密度の向きは逆となるので，概形は(カ)となる。