《理論》〈電磁気〉[R02:問2]鉄心を移動することによるコイルに蓄えられるエネルギーに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，コイルに蓄えられるエネルギーに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

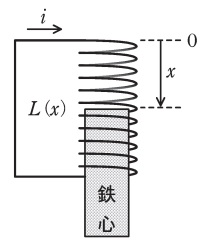
図のようなコイルがあり，鉄心が完全に挿入された状態から$ \ x \ $だけ引き出された時の自己インダクタンスを$ \ L\left( x\right) \ $とする。ただし，鉄心の渦電流，磁気飽和やヒステリシスは無視できるものとする。また，コイルの電気抵抗は無視でき，コイルに流れる電流は電気抵抗によって減衰しないものとする。

鉄心の最初の位置は$ \ x=0 \ $であり，コイルは短絡されて電流$ \ i=I \ $が流れ続けているものとする。このとき，コイルに鎖交する磁束数は$ \ \fbox {　（１）　} \ $で，コイルが蓄えているエネルギーは$ \ \fbox {　（２）　} \ $である。

次に，コイルを短絡したまま，外力を加えて鉄心を$ \ x \ $まで引き出した。このとき，コイルに鎖交する磁束数は$ \ \fbox {　（１）　} \ $のまま変わらないため，電流$ \ i \ $は$ \ \fbox {　（３）　} \ $となり，コイルが蓄えているエネルギーは$ \ \fbox {　（４）　} \ $に変化する。また，外力がした仕事は$ \ \fbox {　（５）　} \ $。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　L\left( 0\right) I　　　　&（ロ）&　\frac {1}{2}\frac {L\left( 0 \right) ^{2}}{L\left( x\right) }I^{2}　　　　&（ハ）&　全て鉄心で熱になった \\[ 5pt ] &（ニ）&　\frac {1}{2}L\left( x\right) I^{2} 　　　　&（ホ）&　\frac {1}{2}L\left( 0\right) I　　　　&（ヘ）&　L\left( 0\right) I^{2} \\[ 5pt ] &（ト）&　L\left( x\right) I^{2}　　　　&（チ）&　0　　　　&（リ）&　全て巻線で熱になった \\[ 5pt ] &（ヌ）&　全てコイルに蓄えられた　　　　　　　　&（ル）&　\frac {L\left( x\right) }{L\left( 0 \right) }I　　　　&（ヲ）&　\frac {1}{4}L\left( 0\right) I^{2} \\[ 5pt ] &（ワ）&　\frac {L\left( 0 \right) }{L\left( x\right) }I　　　　&（カ）&　I　　　&（ヨ）&　\frac {1}{2}L\left( 0\right) I^{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

コイルに蓄えられるエネルギーの変化に関する問題です。
あまり$ \ 3 \ $種では見ないような問題であり，戸惑う受験生も多いかもしれませんが，扱う公式は$ \ 3 \ $種で覚えた公式と変わらない公式です。
しっかりと内容を理解し，(3)や(4)を試験本番までに解けるようにしましょう。

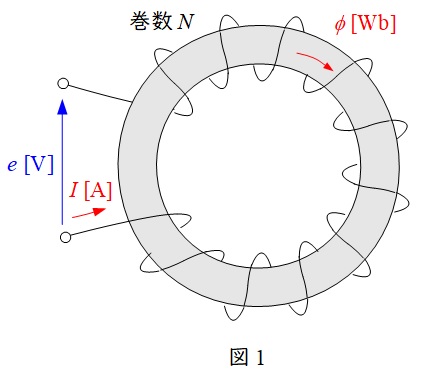
1.自己インダクタンス$ \ L \ $
図1のような環状ソレノイド回路において，巻数$ \ N \ $のコイルに電流$ \ I \ $を流した時の鉄心の磁束$ \ \phi \ $と比例定数$ \ L \ $の関係は，起電力$ \ e \ $を求める関係より，
\[
\begin{eqnarray}
-N\frac {\Delta \phi }{\Delta t}&=&-L\frac {\Delta I}{\Delta t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] L &=&\frac {N\phi }{I} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ L \ $を自己インダクタンスと言います。

2.自己インダクタンス$ \ L \ $と蓄積される電磁エネルギー$ \ W \ $の関係式
自己インダクタンス$ \ L \ $のコイルに電流$ \ I \ $を流し，十分時間が経った時にコイルに蓄積されるエネルギー$ \ W \ $は，
\[
\begin{eqnarray}
W&=&\frac {1}{2}LI^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：イ
ワンポイント解説「1.自己インダクタンス$ \ L \ $」の通り，鎖交する磁束$ \ \varPhi \ $は，
\[
\begin{eqnarray}
\varPhi &=&N\phi \\[ 5pt ] &=&L\left( 0\right) I \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヨ
ワンポイント解説「2.自己インダクタンス$ \ L \ $と蓄積される電磁エネルギー$ \ W \ $の関係式」の通り，コイルに蓄積されるエネルギー$ \ W \ $は，
\[
\begin{eqnarray}
W&=&\frac {1}{2}L\left( 0\right) I^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
題意より，外力を加えて鉄心を$ \ x \ $まで引き出したとき，自己インダクタンスは$ \ L\left( x\right) \ $であり，コイルに鎖交する磁束数は$ \ L\left( 0\right) I \ $のままであるから，
\[
\begin{eqnarray}
L\left( x\right) i&=&L\left( 0\right) I \\[ 5pt ] i&=&\frac {L\left( 0 \right) }{L\left( x\right) }I \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ロ
$ \ x \ $まで引き出したときのコイルに蓄積されるエネルギー$ \ W^{\prime } \ $は，
\[
\begin{eqnarray}
W^{\prime }&=&\frac {1}{2}L\left( x\right) i^{2} \\[ 5pt ] &=&\frac {1}{2}L\left( x\right) \left\{ \frac {L\left( 0 \right) }{L\left( x\right) }I\right\} ^{2} \\[ 5pt ] &=&\frac {1}{2}\frac {L\left( 0 \right) ^{2}}{L\left( x\right) }I^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
題意より，鉄心の渦電流，磁気飽和やヒステリシスは無視できるとなっているので，熱損失は発生せず，外力がした仕事は全てコイルに蓄えられます。