《理論》〈電気回路〉[R02:問5]交流回路における進み及び遅れ無効電力の特性に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，交流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

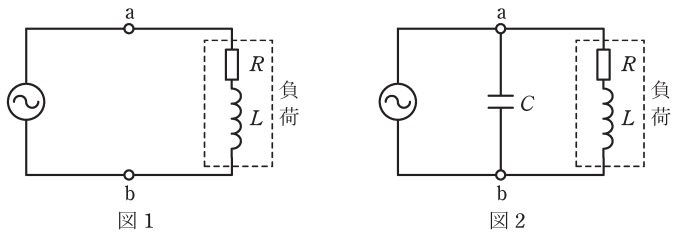
図1の回路において，負荷の抵抗は$ \ R=3 \ \mathrm {\Omega } \ $，有効電力は$ \ 600 \ \mathrm {W} \ $，力率は$ \ 0.6 \ $である。また，電源の角周波数は$ \ \omega \ $である。

この負荷の無効電力は$ \ \fbox {　（１）　} \ \mathrm {var} \ $であり，負荷のリアクタンスは$ \ \omega L= \ \fbox {　（２）　} \ \mathrm {\Omega } \ $である。

図2のように，図1の回路の端子$ \ \mathrm {a－b} \ $にキャパシタ$ \ C \ $を接続すると，電源からみた回路の合成負荷のアドミタンスは，$ \ \displaystyle {\dot Y}=\frac {R}{R^{2}+\left( \omega L \right) ^{2}}+\mathrm {j}\left( \omega C -\frac {\omega L}{R^{2}+\left( \omega L \right) ^{2}}\right) \ $となる。図2において電源からみた回路の合成負荷の力率を$ \ 1 \ $とした。このとき，キャパシタ$ \ C \ $のサセプタンスは$ \ \omega C= \ \fbox {　（３）　} \ \mathrm {S} \ $である。

キャパシタ$ \ C \ $を接続して合成負荷の力率を$ \ 1 \ $にした後に，電源の角周波数$ \ \omega \ $を$ \ \displaystyle \frac {1}{2} \ $倍にすると，電源からみた回路の合成負荷は，力率$ \ \fbox {　（４）　} \ $の$ \ \fbox {　（５）　} \ $負荷となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　0.16　　　　　　&（ロ）&　0.12　　　　　　&（ハ）&　1 \\[ 5pt ] &（ニ）&　5　　　　　　&（ホ）&　600　　　　　　&（ヘ）&　容量性 \\[ 5pt ] &（ト）&　6.25　　　　　　&（チ）&　誘導性　　　　　　&（リ）&　3 \\[ 5pt ] &（ヌ）&　4　　　　　　&（ル）&　800　　　　　　&（ヲ）&　400 \\[ 5pt ] &（ワ）&　0.952　　　　　　&（カ）&　抵抗　　　　　　&（ヨ）&　0.192 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

交流回路における各インピーダンスと無効電力の変化に関する問題です。
難易度は標準程度か迷いましたが，$ \ 2 \ $種受験生としては解いて欲しいと思う期待もこめて★２つとしています。
ぜひ(5)まで完答できるよう習得して下さい。

1.皮相電力，有効電力，無効電力
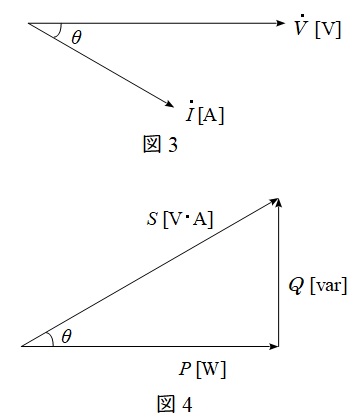
図3のような電圧$ \ V \ $，電流$ \ I \ $，電圧と電流の位相差が$ \ \theta \ $(電流が遅れ)のベクトル図が与えられている時，皮相電力$ \ S \ $，有効電力$ \ P \ $，無効電力$ \ Q \ $は図4のように描くことができ，力率を$ \ \cos \theta \ $とすると，
\[
\begin{eqnarray}
S &=&VI \\[ 5pt ] P &=&VI\cos \theta \\[ 5pt ] Q &=&VI\sin \theta \\[ 5pt ] \end{eqnarray}
\] となり，
\[
\begin{eqnarray}
S &=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.抵抗，コイル，コンデンサのインピーダンスとアドミタンス
抵抗$ \ R \ \mathrm {[\Omega ]} \ $，コイル$ \ L \ \mathrm {[H]} \ $，コンデンサ$ \ C \ \mathrm {[F]} \ $があり，電源周波数$ \ f \ \mathrm {[Hz]} \ $が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ] &=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれのアドミタンスは，
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {R}}&=&\frac {1}{R} \\[ 5pt ] {\dot Y}_{\mathrm {L}}&=&\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1}{\mathrm {j}2\pi f L} \\[ 5pt ] {\dot Y}_{\mathrm {C}}&=&\mathrm {j}\omega C \\[ 5pt ] &=&\mathrm {j}2\pi f C \\[ 5pt ] \end{eqnarray}
\] で求められます。

【関連する「電気の神髄」記事】

　　有効電力・無効電力・複素電力

【解答】

(1)解答：ル
ワンポイント解説「1.皮相電力，有効電力，無効電力」より，無効電力$ \ Q \ $の大きさは，
\[
\begin{eqnarray}
Q &=&P\tan \theta \\[ 5pt ] &=&P\cdot \frac {\sin \theta }{\cos \theta } \\[ 5pt ] &=&P\cdot \frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta } \\[ 5pt ] &=&600\times \frac {\sqrt {1-0.6 ^{2} }}{0.6 } \\[ 5pt ] &=&600\times \frac {0.8}{0.6} \\[ 5pt ] &=&800 \ \mathrm {[var]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヌ
(1)より，$ \ \displaystyle \tan \theta = \frac {0.8}{0.6}=\frac {4}{3} \ $であるから，ワンポイント解説「2.抵抗，コイル，コンデンサのインピーダンスとアドミタンス」より，
\[
\begin{eqnarray}
\frac {\omega L}{R} &=&\tan \theta \\[ 5pt ] \frac {\omega L}{3} &=&\frac {4}{3} \\[ 5pt ] \omega L&=&4 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：イ
合成負荷のアドミタンスの力率が$ \ 1 \ $であるためには，アドミタンスの虚数項（サセプタンス）が零でなければならないので，
\[
\begin{eqnarray}
\omega C -\frac {\omega L}{R^{2}+\left( \omega L \right) ^{2}} &=&0 \\[ 5pt ] \omega C &=&\frac {\omega L}{R^{2}+\left( \omega L \right) ^{2}} \\[ 5pt ] &=&\frac {4}{3^{2}+4 ^{2}} \\[ 5pt ] &=&0.16 \ \mathrm {[S]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ワ
電源の角周波数$ \ \omega \ $を$ \ \displaystyle \frac {1}{2} \ $倍にすると，電源からみた回路の合成負荷のアドミタンス$ \ \displaystyle {\dot Y}^{\prime } \ $は，
\[
\begin{eqnarray}
\displaystyle {\dot Y}^{\prime } &=&\frac {R}{\displaystyle R^{2}+\left( \frac {1}{2}\omega L \right) ^{2}}+\mathrm {j}\left( \frac {1}{2}\omega C -\frac {\displaystyle \frac {1}{2}\omega L}{\displaystyle R^{2}+\left( \frac {1}{2}\omega L \right) ^{2}}\right) \\[ 5pt ] &=&\frac {3}{\displaystyle 3^{2}+\left( \frac {1}{2}\times 4 \right) ^{2}}+\mathrm {j}\left( \frac {1}{2}\times 0.16 -\frac {\displaystyle \frac {1}{2}\times 4}{\displaystyle 3^{2}+\left( \frac {1}{2}\times 4 \right) ^{2}}\right) \\[ 5pt ] &=&\frac {3}{9+4}+\mathrm {j}\left( 0.08 -\frac {2}{9+4}\right) \\[ 5pt ] &≒&0.23077-\mathrm {j}0.073846 \ \mathrm {[S]} \\[ 5pt ] \end{eqnarray}
\] となるので，力率$ \ \cos \theta \ $は
\[
\begin{eqnarray}
\cos \theta &=&\frac {0.23077}{\sqrt {0.23077^{2}+0.073846^{2}}} \\[ 5pt ] &≒&\frac {0.23077}{0.24230} \\[ 5pt ] &≒&0.952 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：チ
電源からみた回路の合成負荷のアドミタンスは，$ \ \displaystyle {\dot Y}^{\prime }=0.23077-\mathrm {j}0.073846 \ \mathrm {[S]} \ $であり，虚数項がマイナスなので誘導性であることがわかる。