【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,直流ブリッジを用いた抵抗測定に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
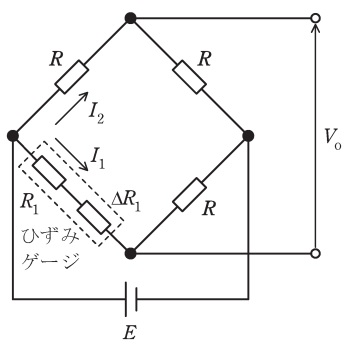
図は,ひずみにより微小な抵抗変化を生じるひずみゲージを用いた測定回路である。このような抵抗の測定には,図のような\( \ \fbox { (1) } \ \)ブリッジの原理が使用される。
図において,直流電圧源を\( \ E \ \),回路の電流を\( \ I_{1} \ \),\( \ I_{2} \ \)とする。ひずみがなく,ひずみゲージの固定抵抗\( \ R_{1} \ \)の変化\( \ \Delta R_{1} \ \)が\( \ \Delta R_{1}=0 \ \)の場合,ブリッジの出力電圧\( \ V_{\mathrm {o}} \ \)を\( \ R_{1} \ \),\( \ R \ \),\( \ E \ \)を用いて表すと,
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& \ \fbox { (2) } \ ・・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。ただし,周囲温度の変化による各抵抗の変化は無視できるものとする。
次に,ひずみが生じ,\( \ R_{1} \ \)が\( \ \left( R_{1}+\Delta R_{1} \right) \ \)になった場合を考える。
\( \ R_{1}=R \ \)となるようなひずみゲージを選べば,\(①\)式より\( \ V_{\mathrm {o}} \ \)は
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& \ \fbox { (3) } \ ・・・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで、通常,\( \ R_{1} ≫ \Delta R_{1} \ \)であることから,\(②\)式より\( \ V_{\mathrm {o}} \ \)は
\[
\begin{eqnarray}
V_{\mathrm {o}} &≒& \ \fbox { (4) } \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \Delta R_{1} \ \)に比例した電圧が得られる。
したがって,\( \ R_{1}=R=100 \ \mathrm {\Omega } \ \),\( \ E=2 \ \mathrm {V} \ \)であるとき,ある大きさのひずみにより,\( \ 0.2 \ \mathrm {%} \ \)の抵抗増加が\( \ R_{1} \ \)に生じたとすれば,\( \ \fbox { (5) } \ \mathrm {mV} \ \)の出力電圧\( \ V_{\mathrm {o}} \ \)が得られる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& ウィーン &(ロ)& ホイートストン &(ハ)& \frac {R_{1}-R}{2\left( R_{1}+R\right) }E \\[ 5pt ]
&(ニ)& \frac {\Delta R_{1}}{\left( 2R+\Delta R_{1}\right) }E &(ホ)& \frac {R_{1}}{2\left( R_{1}+R\right) }E &(ヘ)& \frac {\Delta R_{1}}{4R}E \\[ 5pt ]
&(ト)& \frac {\Delta R_{1}}{\left( 4R+2\Delta R_{1}\right) }E &(チ)& \frac {R_{1}-R}{\left( R_{1}+R\right) }E &(リ)& 2.0 \\[ 5pt ]
&(ヌ)& \frac {\Delta R_{1}}{\left( R+\Delta R_{1}\right) }E &(ル)& 1.0 &(ヲ)& シェーリング \\[ 5pt ]
&(ワ)& 20.0 &(カ)& \frac {\Delta R_{1}}{R}E &(ヨ)& \frac {\Delta R_{1}}{2R}E \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
ホイートストンブリッジをはじめとするブリッジ回路に関する問題は,過去何回も出題されており,電気電子計測の分野では一番出題確率が高い分野ではないかと思います。
具体的には平成28年問8や平成27年問8,平成26年問6で出題されており,それぞれ静電容量や周波数といった違うものを測定し,回路も若干異なることがわかると思います。
1.直流ブリッジの平衡条件
直流ブリッジ回路は抵抗の抵抗値を求める方法であり,ホイートストンブリッジと呼ばれます。
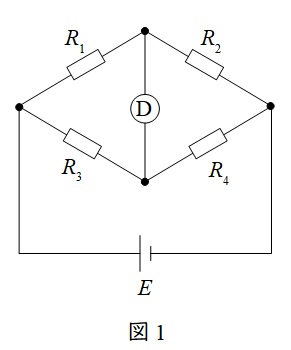
図1の回路において,検出器\( \ Ⓓ \ \)に電流が流れない条件を平衡条件と言い,
\[
\begin{eqnarray}
R_{1}R_{4} &=& R_{2}R_{3} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。したがって,3つの既知の抵抗があれば,残りの1つの抵抗値を求めることができます。
※ 本問では平衡条件は使用しませんが,必須の知識となるので覚えておきましょう。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ロ
題意より,解答候補は(イ)ウィーン,(ロ)ホイートストン,(ヲ)シェーリング,となると思います。抵抗値の測定する方法はホイートストンブリッジといい,ウィーンブリッジは電源の周波数を求める方法,シェ-リングブリッジはコンデンサの静電容量を求める方法です。
(2)解答:ハ
分圧の法則より,図2の\( \ V_{\mathrm {a}} \ \)及び\( \ V_{\mathrm {b}} \ \)の電圧は,
\[
\begin{eqnarray}
V_{\mathrm {a}} &=& \frac {R}{R+R}E \\[ 5pt ]
&=& \frac {1}{2}E \\[ 5pt ]
V_{\mathrm {b}} &=& \frac {R}{R_{1}+R}E \\[ 5pt ]
\end{eqnarray}
\]
であるから,ブリッジの出力電圧\( \ V_{\mathrm {o}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& V_{\mathrm {a}}-V_{\mathrm {b}} \\[ 5pt ]
&=& \frac {1}{2}E-\frac {R}{R_{1}+R}E \\[ 5pt ]
&=& \frac {R_{1}+R-2R}{2\left( R_{1}+R\right) }E \\[ 5pt ]
&=& \frac {R_{1}-R}{2\left( R_{1}+R\right) }E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。

(3)解答:ト
(2)解答式を\( \ R_{1} \ → \ \left( R_{1}+\Delta R_{1} \right) \ \)とし,\( \ R_{1} \ → \ R \ \)とすれば良いので,
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& \frac {\left( R_{1}+\Delta R_{1} \right) -R}{2\left\{ \left( R_{1}+\Delta R_{1} \right) +R\right\} }E \\[ 5pt ]
&=& \frac {\left( R+\Delta R_{1} \right) -R}{2\left\{ \left( R+\Delta R_{1} \right) +R\right\} }E \\[ 5pt ]
&=& \frac {\Delta R_{1} }{2\left( 2R+\Delta R_{1}\right) }E \\[ 5pt ]
&=& \frac {\Delta R_{1}}{\left( 4R+2\Delta R_{1}\right) }E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※ 選択肢に合わせ,分母にカッコをつけています。
(4)解答:ヘ
(3)の解答式において,題意より\( \ R_{1} ≫ \Delta R_{1} \ \)であるから,分母の\( \ \Delta R_{1} \ \)を無視すると,
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& \frac {\Delta R_{1}}{4R+2\Delta R_{1}}E \\[ 5pt ]
&≃& \frac {\Delta R_{1}}{4R}E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ル
\( \ 0.2 \ \mathrm {%} \ \)の抵抗増加が\( \ R_{1} \ \)に生じたとなっているので,\( \ \Delta R_{1} \ \)は,
\[
\begin{eqnarray}
\Delta R_{1} &=& \frac {0.2}{100}R_{1} \\[ 5pt ]
&=& \frac {0.2}{100}\times 100 \\[ 5pt ]
&=& 0.2 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,(4)解答式より,出力電圧\( \ V_{\mathrm {o}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& \frac {\Delta R_{1}}{4R}E \\[ 5pt ]
&=& \frac {0.2}{4\times 100}\times 2 \\[ 5pt ]
&=& 0.001 \ \mathrm {[V]} → 1 \ \mathrm {[mV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは