Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
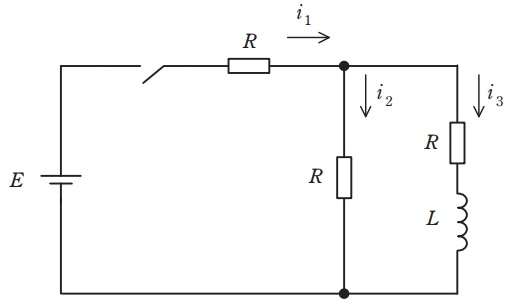
図に示すような,抵抗,コイル,直流電圧源,及びスイッチからなる回路を考える。初期状態ではスイッチは開いており,回路には電流は流れていないものとする。
時刻\( \ t=0 \ \)でスイッチを閉じると,図に示す電流\( \ i_{1} \ \),\( \ i_{2} \ \),\( \ i_{3} \ \)について
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
i_{1}=i_{2}+i_{3} &・・・・・・・・・・・・・・ ①& \\
\displaystyle Ri_{2}=Ri_{3}+L\frac {\mathrm {d}i_{3}}{\mathrm {d}t} &・・・・・・・・・・・・・・ ②& \\
\displaystyle E=Ri_{1}+Ri_{2} &・・・・・・・・・・・・・・ ③& \\
\end{array}
\right.
\end{eqnarray}
\]
という式が得られる。③式に①式を代入し,さらに②式を代入すると,③式は\( \ i_{3} \ \)を用いて,
\[
\begin{eqnarray}
E&=& \ \fbox { (1) } \ i_{3} + \ \fbox { (2) } \ \frac {\mathrm {d}i_{3}}{\mathrm {d}t} ・・・・・・・・・ ③^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
と表すことができる。 \( \ i_{3}\left( 0 \right) =0 \ \)であることを考慮すると\( \ i_{3}\left( t \right) \ \)は,
\[
\begin{eqnarray}
i_{3}\left( t \right) &=& \ \fbox { (3) } \ \times \displaystyle \left( 1-\mathrm {e}^{-\frac {t}{\tau _{1}}}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。ここで\( \ \tau _{1}=\fbox { (4) } \ \)である。
スイッチを閉じてから十分な時間が経過した時刻\( \ t=T \ \)にスイッチを開くと,\( \ t≧T \ \)における\( \ i_{3}\left( t \right) \ \)は
\[
\begin{eqnarray}
i_{3}\left( t \right) &=& \ \fbox { (3) } \ \times \displaystyle \mathrm {e}^{-\frac {t-T}{\tau _{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \tau _{2}=\fbox { (5) } \ \)である。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {E}{3R} &(ロ)& \frac {3L}{R} &(ハ)& LR \\[ 5pt ]
&(ニ)& \frac {E}{R} &(ホ)& L &(ヘ)& R \\[ 5pt ]
&(ト)& 3L &(チ)& \frac {L}{2R} &(リ)& \frac {2E}{R} \\[ 5pt ]
&(ヌ)& 2LR &(ル)& 2R &(ヲ)& \frac {2R}{L} \\[ 5pt ]
&(ワ)& 3R &(カ)& 2L &(ヨ)& \frac {2L}{3R} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
毎年定番となっている過渡現象からの出題です。
\( \ i_{2} \ \)の抵抗がなければ相当易しい問題となりますが,\( \ i_{2} \ \)が受験生を考えさせる問題となっています。
まともに微分方程式を解くと時間がかかる問題ですが,(5)等は初期条件を求めずに時定数を導出する等の工夫をして大問\( \ 1 \ \)問あたり\( \ 15 \ \)分以内には解き終えたいところです。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
過渡現象における\( \ RLC \ \)それぞれの電圧は,線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ v_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ v_{\mathrm{L}} \ \),リアクトル\( \ C \ \)の電圧\( \ v_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ]
v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,一般解\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解すなわち\( \ L \ \)開放(\( \ E=0 \ \)と同義)の時の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となった場合,両辺とも対数を外すと,
\[
\begin{eqnarray}
x&=&A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ワ
(2)解答:カ
③式に①式を代入すると,
\[
\begin{eqnarray}
E&=&Ri_{1}+Ri_{2} \\[ 5pt ]
&=&R\left( i_{2}+i_{3}\right)+Ri_{2} \\[ 5pt ]
&=&Ri_{2}+Ri_{3}+Ri_{2} \\[ 5pt ]
&=&2Ri_{2}+Ri_{3} \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに②式を代入すると,
\[
\begin{eqnarray}
E&=&2Ri_{2}+Ri_{3} \\[ 5pt ]
&=&2\left( Ri_{3}+L\frac {\mathrm {d}i_{3}}{\mathrm {d}t}\right) +Ri_{3} \\[ 5pt ]
&=&2Ri_{3}+2L\frac {\mathrm {d}i_{3}}{\mathrm {d}t}+Ri_{3} \\[ 5pt ]
&=&3Ri_{3}+2L\frac {\mathrm {d}i_{3}}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:イ
(1)及び(2)の解答式について,定常解\( \ i_{\mathrm {3s}} \ \)は,\( \ \displaystyle \frac {\mathrm {d}i_{3}}{\mathrm {d}t}=0 \ \)とすると,
\[
\begin{eqnarray}
E&=&3Ri_{\mathrm {3s}} \\[ 5pt ]
i_{\mathrm {3s}}&=&\frac {E}{3R} \\[ 5pt ]
\end{eqnarray}
\]
であり,過渡解\( \ i_{\mathrm {3t}} \ \)を求める関係式は,\( \ \displaystyle E=0 \ \)とすると,
\[
\begin{eqnarray}
0&=&3Ri_{\mathrm {3t}}+2L\frac {\mathrm {d}i_{\mathrm {3t}}}{\mathrm {d}t} \\[ 5pt ]
2L\frac {\mathrm {d}i_{\mathrm {3t}}}{\mathrm {d}t}&=&-3Ri_{\mathrm {3t}} \\[ 5pt ]
\frac {1}{i_{\mathrm {3t}}}\mathrm {d}i_{\mathrm {3t}}&=&-\frac {3R}{2L}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺積分すると,ワンポイント解説「3.自然対数の微分積分」の通り,
\[
\begin{eqnarray}
\int \frac {1}{i_{\mathrm {3t}}}\mathrm {d}i_{\mathrm {3t}}&=&\int -\frac {3R}{2L}\mathrm {d}t \\[ 5pt ]
\ln i_{\mathrm {3t}}&=&-\frac {3R}{2L}t+C \ \left( C \ は積分定数\right) \\[ 5pt ]
i_{\mathrm {3t}}&=&A\mathrm {e}^{-\frac {3R}{2L}t} \ \left( A \ は積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
なる。よって,一般解\( \ i_{\mathrm {3}} \ \)は,ワンポイント解説「2.過渡現象における定常解と過渡解」の通り,
\[
\begin{eqnarray}
i_{\mathrm {3}}&=&i_{\mathrm {3s}}+i_{\mathrm {3t}} \\[ 5pt ]
&=&\frac {E}{3R}+A\mathrm {e}^{-\frac {3R}{2L}t} \\[ 5pt ]
\end{eqnarray}
\]
となるので,初期条件\( \ i_{3}\left( 0 \right) =0 \ \)より,
\[
\begin{eqnarray}
0&=&\frac {E}{3R}+A\mathrm {e}^{-\frac {3R}{2L}\times 0} \\[ 5pt ]
0&=&\frac {E}{3R}+A \\[ 5pt ]
A&=&-\frac {E}{3R} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
i_{\mathrm {3}}&=&\frac {E}{3R}-\frac {E}{3R}\mathrm {e}^{-\frac {3R}{2L}t} \\[ 5pt ]
&=&\frac {E}{3R}\left( 1-\mathrm {e}^{-\frac {3R}{2L}t}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
(3)の解答式より,\( \ \displaystyle \tau _{1}=\frac {2L}{3R} \ \)と求められる。
(5)解答:チ
\( \ t≧T \ \)における回路方程式から,
\[
\begin{eqnarray}
Ri_{\mathrm {3}}+L\frac {\mathrm {d}i_{3}}{\mathrm {d}t}+Ri_{3}&=&0 \\[ 5pt ]
L\frac {\mathrm {d}i_{3}}{\mathrm {d}t}&=&-2Ri_{3} \\[ 5pt ]
\frac {1}{i_{3}}\mathrm {d}i_{3}&=&-\frac {2R}{L}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺積分すると,ワンポイント解説「3.自然対数の微分積分」の通り,
\[
\begin{eqnarray}
\int \frac {1}{i_{3}}\mathrm {d}i_{3}&=&\int -\frac {2R}{L}\mathrm {d}t \\[ 5pt ]
\ln i_{3}&=&-\frac {2R}{L}t+C^{\prime } \ \left( C^{\prime } \ は積分定数\right) \\[ 5pt ]
i_{3}&=&A^{\prime }\mathrm {e}^{-\frac {2R}{L}t} \ \left( A^{\prime } \ は積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。(3)の定常解より\( \ \displaystyle i_{3}\left( T\right) =\frac {E}{3R} \ \)であるから,
\[
\begin{eqnarray}
\frac {E}{3R}&=&A^{\prime }\mathrm {e}^{-\frac {2R}{L}T} \\[ 5pt ]
A^{\prime }&=&\frac {E}{3R}\mathrm {e}^{\frac {2R}{L}T} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
i_{3}&=&\frac {E}{3R}\mathrm {e}^{\frac {2R}{L}T}\mathrm {e}^{-\frac {2R}{L}t} \\[ 5pt ]
&=&\frac {E}{3R}\mathrm {e}^{-\frac {2R}{L}\left( t-T\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められ,\( \ \displaystyle \tau _{2}=\frac {L}{2R} \ \)となる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは