【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,無限長の直線電流が作る磁束に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。ただし,真空中の透磁率を\( \ \mu_ {0} \ \)とする。
真空中に無限長の直線電流\( \ I \ \)が流れている。このとき,直線電流から距離\( \ r \left( r>0 \right) \ \)離れた場所の磁束密度の大きさ\( \ B \left( r \right) \ \)は,①式である。
\[
\begin{eqnarray}
B\left( r \right) &=& \ \fbox { (1) } \ ・・・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
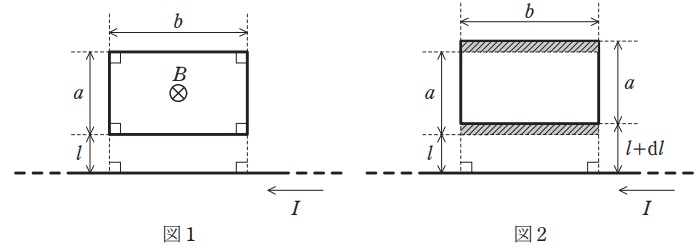
次に,直線電流と同一平面上に,図1のような巻数\( \ 1 \ \)の長方形コイルを置く。ただし,コイルの導体は十分細く,コイルに流れる電流は十分小さいものとする。直線電流が作り出す磁束のうち,直線電流から距離\( \ l \ \)離れた長方形コイルに鎖交する磁束を\( \ \mathit {\Phi } \left( l \right) \ \)とする。ただし,紙面の手前から奥に鎖交する磁束の向きを正とする。
ここで,図2のように,長方形コイルを\( \ \mathrm {d}l \ \)だけ直線電流から微小に遠ざけたときの鎖交磁束の変化\( \ \mathrm {d}\mathit {\Phi } \left( l \right) \ \)を考える。図2において,ハッチングした領域の磁束の増減を考えれば良いので,\( \ B \ \)を用いて\( \ \mathrm {d}\mathit {\Phi } \left( l \right) = \ \fbox { (2) } \ b\mathrm {d}l \ \)と表せる。これより,②式が成り立つ。
\[
\begin{eqnarray}
\frac {\mathrm {d}\mathit {\Phi } \left( l \right) }{\mathrm {d}l } &=& \ \fbox { (2) } \ b \ \ ・・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
ここで,\( \ t \ \)を時間とする。コイルが速度\( \ v \ \)で直線電流から遠ざかっているとき③式が成り立つ。
\[
\begin{eqnarray}
v &=& \ \fbox { (3) } \ ・・・・・・・・・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
ファラデーの法則により,コイルに誘起される電圧\( \ V \left( l \right) \ \)は④式で表せる。
\[
\begin{eqnarray}
V \left( l \right) &=& \ \fbox { (4) } \ ・・・・・・・・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
④式に①式,②式及び③式を代入すると,\( \ V \left( l \right) \ \)は⑤式のように計算できる。
\[
\begin{eqnarray}
V \left( l \right) &=& \ \fbox { (5) } \ ・・・・・・・・・・・・・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \left[ B\left( l+a\right) -B\left( l\right) \right] &(ロ)& -\frac {\mathrm {d}\mathit {\Phi } \left( l \right) }{\mathrm {d}t } &(ハ)& \frac {\mu_ {0}I}{2r} \\[ 5pt ]
&(ニ)& \frac {\mathrm {d}l}{\mathrm {d}t} &(ホ)& \frac {\mu_ {0}I}{\pi r^{2}} &(ヘ)& -\frac {\mathrm {d}\mathit {\Phi } \left( l \right) }{\mathrm {d}a } \\[ 5pt ]
&(ト)& \frac {\mu _{0}abvI}{\pi l^{2}\left( l+a\right) } &(チ)& \frac {\mathrm {d}a}{\mathrm {d}t} &(リ)& \frac {\mathrm {d}b}{\mathrm {d}t} \\[ 5pt ]
&(ヌ)& \left[ B\left( l+\mathrm {d}l\right) -B\left( l\right) \right] &(ル)& \frac {\mu _{0}abvI}{2l\left( l+a\right) } &(ヲ)& -\frac {\mathrm {d}\mathit {\Phi } \left( l \right) }{\mathrm {d}l } \\[ 5pt ]
&(ワ)& \frac {\mu_ {0}I}{2\pi r} &(カ)& \left[ B\left( l+b\right) -B\left( l\right) \right] &(ヨ)& \frac {\mu _{0}abvI}{2\pi l\left( l+a\right) } \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
無限長の直線電流が作る磁束に関する問題です。
\( \ 3 \ \)種の頃にはあまり出て来なかった概念が出題されているので,微分積分の考え方を理解していない受験生には苦しい問題であったかなという印象です。
一方で,しっかりと理解していれば完答も狙えるいかにも\( \ 2 \ \)種らしい良問と言えるかなと思います。
1.アンペア(アンペール)の周回積分の法則
空間上の磁界ベクトルを\( \ \boldsymbol H \ \),\( \ \mathrm {C} \ \)を閉曲線,\( \ \mathrm {d}\boldsymbol l \ \)を\( \ \mathrm {C} \ \)上の微小区間ベクトル,\( \ I \ \)を\( \ \mathrm {C} \ \)と鎖交する電流の総量とすると,
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,これをアンペアの周回積分の法則といいます。
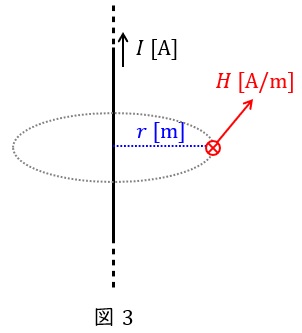
例えば,図3のように無限長直線電流\( \ I \ \mathrm {[A]} \ \)が流れているとき,電線から距離\( \ r \ \mathrm {[m]} \ \)の位置での磁界の強さ\( \ H \ \mathrm {[A / m]} \ \)は,\( \ l=2\pi r \ \)なので,
\[
\begin{eqnarray}
2\pi r H&=&I \\[ 5pt ]
H&=&\frac {I}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.磁束密度\( \ B \ \)
単位面積あたりに通過する磁束のことで,微小な面積\( \ \mathrm {d}\boldsymbol S \ \)を通過する磁束が\( \ \mathrm {d}\mathit {\Phi } \ \)であるとき,磁束密度\( \ \boldsymbol B \ \)との関係は,
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi }&=&\boldsymbol B\cdot \mathrm {d}\boldsymbol S \\[ 5pt ]
\mathit {\Phi }&=&\int_{\mathrm {S}} \boldsymbol B\cdot \mathrm {d}\boldsymbol S \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係
透磁率が\( \ \mu \ \mathrm {[H / m]} \ \)の時,磁束密度\( \ B \ \mathrm {[T]} \ \)と磁界の大きさ\( \ H \ \mathrm {[A / m]} \ \)の関係は,
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)
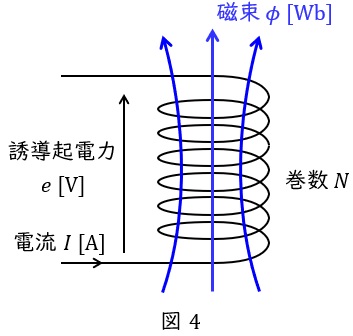
図4において,巻数\( \ N \ \)のコイルを貫通する磁束\( \ \phi \ \mathrm {[Wb]} \ \)があるとき,ファラデーの電磁誘導の法則より,コイルに発生する誘導起電力\( \ e \ \mathrm {[V]} \ \)は,磁束の時間変化に比例し,
\[
\begin{eqnarray}
e&=&−N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。これをファラデーの電磁誘導の法則といいます。このとき,電流変化によりコイル内の磁束が変化したと考えれば,
\[
\begin{eqnarray}
e&=&−L\frac {\mathrm {d}I }{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
という関係も成り立ち,\( \ L \ \mathrm {[H]} \ \)を自己インダクタンスと言います。これらの関係から,
\[
\begin{eqnarray}
−N\frac {\mathrm {d}\phi }{\mathrm {d}t}&=&−L\frac {\mathrm {d}I }{\mathrm {d}t} \\[ 5pt ]
N\phi &=&LI \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(1)解答:ワ
直線電流から距離\( \ r \ \)離れた場所の磁界の大きさ\( \ H \left( r \right) \ \)は,ワンポイント解説「1.アンペア(アンペール)の周回積分の法則」の通り,
\[
\begin{eqnarray}
H \left( r \right) &=&\frac {I}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
であるから,磁束密度の大きさ\( \ B \left( r \right) \ \)は,ワンポイント解説「3.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係」の通り,
\[
\begin{eqnarray}
B\left( r \right) &=&\mu _{0} H\left( r \right) \\[ 5pt ]
&=&\frac {\mu_ {0}I}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:イ
鎖交磁束の変化は,図2における\( \ 2 \ \)つのハッチングした領域を通過する磁束の差である。面積\( \ \mathrm {d}S \ \)はともに,
\[
\begin{eqnarray}
\mathrm {d}S&=&b\mathrm {d}l \\[ 5pt ]
\end{eqnarray}
\]
であり,通過する磁束が増える部分の磁束密度が\( \ B \left( l+a \right) \ \),通過する磁束が減る部分の磁束密度が\( \ B \left( l \right) \ \)であるから,鎖交磁束の変化\( \ \mathrm {d}\mathit {\Phi } \left( l \right) \ \)は,
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi } \left( l \right) &=&B \left( l+a \right) \mathrm {d}S-B \left( l \right) \mathrm {d}S \\[ 5pt ]
&=&\left[ B\left( l+a \right) -B \left( l \right) \right] \mathrm {d}S \\[ 5pt ]
&=&\left[ B\left( l+a \right) -B \left( l \right) \right] b\mathrm {d}l \\[ 5pt ]
\frac {\mathrm {d}\mathit {\Phi } \left( l \right) }{\mathrm {d}l}&=&\left[ B\left( l+a \right) -B \left( l \right) \right] b \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ニ
速度\( \ v \ \)は位置の時間変化であるから,今回は\( \ \mathrm {d}t \ \)の間に\( \ \mathrm {d}l \ \)変化したので,
\[
\begin{eqnarray}
v&=&\frac {\mathrm {d}l}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ロ
本問のコイルは巻き数\( \ 1 \ \)であるから,ファラデーの電磁誘導の法則より,コイルに誘起される電圧\( \ V \left( l \right) \ \)は,ワンポイント解説「4.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)」の通り,
\[
\begin{eqnarray}
V \left( l \right) &=&−\frac {\mathrm {d}\mathit {\Phi } \left( l \right) }{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
(4)解答式を計算していくと,
\[
\begin{eqnarray}
V \left( l \right) &=&−\frac {\mathrm {d}\mathit {\Phi } \left( l \right) }{\mathrm {d}t} \\[ 5pt ]
&=&−\frac {\mathrm {d}\mathit {\Phi } \left( l \right) }{\mathrm {d}l}\cdot \frac {\mathrm {d}l}{\mathrm {d}t} \\[ 5pt ]
&=&−\left[ B\left( l+a \right) -B \left( l \right) \right] b\cdot v \\[ 5pt ]
&=&−\left\{ \frac {\mu_ {0}I}{2\pi \left( l+a \right) }-\frac {\mu_ {0}I}{2\pi l} \right\} b\cdot v \\[ 5pt ]
&=&−\frac {\mu_ {0}bvI}{2\pi }\left( \frac {1}{l+a}-\frac {1}{l} \right) \\[ 5pt ]
&=&−\frac {\mu_ {0}bvI}{2\pi }\cdot \frac {l-\left( l+a\right) }{l\left( l+a\right) } \\[ 5pt ]
&=&\frac {\mu _{0}abvI}{2\pi l\left( l+a\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは