Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,正弦波交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
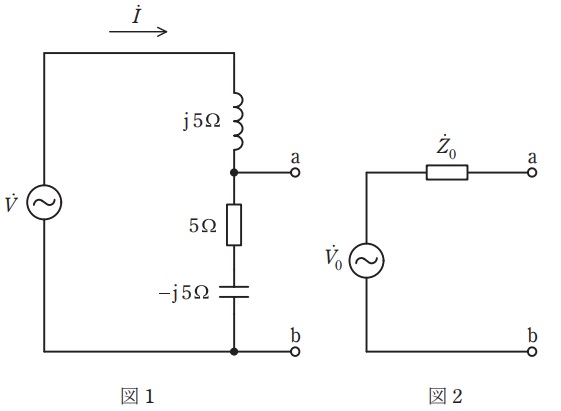
図1の回路において,電源電圧\( \ \dot V=10∠0=10 \ \mathrm {V} \ \)であり,各素子のインピーダンスは図1に示すとおりである。図1の回路において,電流\( \ \dot I= \ \fbox { (1) } \ \mathrm {A} \ \)である。
図1の回路の端子\( \ \mathrm {a – b} \ \)に負荷\( \ {\dot Z}_{\mathrm {L}}=5+\mathrm {j}5 \ \mathrm {\Omega } \ \)を接続したときに,負荷\( \ {\dot Z}_{\mathrm {L}} \ \)を流れる電流\( \ {\dot I}_{\mathrm {L}} \ \)と負荷\( \ {\dot Z}_{\mathrm {L}} \ \)で消費される有効電力\( \ P_{\mathrm {L}} \ \)を,以下の手順に従って求める。
端子\( \ \mathrm {a – b} \ \)から見込んだ図1の等価回路は図2となる。ただし,図2の等価回路において\( \ {\dot V}_{\mathrm {0}} = \ \fbox { (2) } \ \mathrm {V} \ \),\( \ {\dot Z}_{\mathrm {0}} = \ \fbox { (3) } \ \mathrm {\Omega } \ \)である。
したがって,求める電流\( \ {\dot I}_{\mathrm {L}} \ \)と有効電力\( \ P_{\mathrm {L}} \ \)は,図2の等価回路の端子\( \ \mathrm {a – b} \ \)に負荷\( \ {\dot Z}_{\mathrm {L}} \ \)を接続したときに,負荷\( \ {\dot Z}_{\mathrm {L}} \ \)を流れる電流,及び負荷\( \ {\dot Z}_{\mathrm {L}} \ \)で消費される有効電力として,\( \ {\dot I}_{\mathrm {L}}= \ \fbox { (4) } \ \mathrm {A} \ \),及び \( \ P_{\mathrm {L}}= \ \fbox { (5) } \ \mathrm {W} \ \)と求められる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& -\mathrm {j} &(ロ)& 5+\mathrm {j}5 &(ハ)& 10+\mathrm {j}10 \\[ 5pt ]
&(ニ)& 2-\mathrm {j}2 &(ホ)& 5 &(ヘ)& \mathrm {j} \\[ 5pt ]
&(ト)& 2 &(チ)& -10-\mathrm {j}10 &(リ)& 5-\mathrm {j}5 \\[ 5pt ]
&(ヌ)& 10-\mathrm {j}10 &(ル)& 1+\mathrm {j} &(ヲ)& \mathrm {j}5 \\[ 5pt ]
&(ワ)& 2+\mathrm {j}2 &(カ)& 20 &(ヨ)& 10 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
テブナンの定理を利用した交流回路の演算に関する問題です。
交流回路の各素子のインピーダンスや電力の求め方,合成インピーダンス,分圧の法則等はここではカバーしきれないため\( \ 3 \ \)種の問題や参考書を参考にするようにして下さい。
1.テブナンの定理
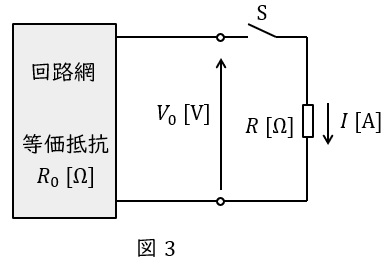
図3のような回路において,端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \),端子\( \ \mathrm {a-b} \ \)から電源側をみた合成抵抗を\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)とする(ただし,電圧源は短絡,電流源は開放する)と,図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流の大きさ\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。この関係は抵抗のみでなく,リアクタンスにも適用可能です。
【解答】
(1)解答:ト
図1における合成インピーダンス\( \ {\dot Z}_{\mathrm {1}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {1}}&=&\mathrm {j}5+5-\mathrm {j}5 \\[ 5pt ]
&=&5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
なので,電流\( \ \dot I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
\dot I&=&\frac {\dot V}{{\dot Z}_{\mathrm {1}}} \\[ 5pt ]
&=&\frac {10}{5} \\[ 5pt ]
&=&2 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヌ
端子\( \ \mathrm {a – b} \ \)に加わる電圧\( \ {\dot V}_{\mathrm {0}} \ \mathrm {[V]} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {0}}&=&\frac {5-\mathrm {j}5}{{\dot Z}_{\mathrm {1}}}\dot V \\[ 5pt ]
&=&\frac {5-\mathrm {j}5}{5}\times 10 \\[ 5pt ]
&=&10-\mathrm {j}10 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ロ
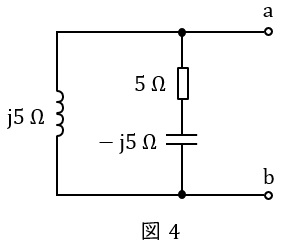
端子\( \ \mathrm {a – b} \ \)から電源側を見た等価抵抗は電圧源を短絡すれば良いので,図4のようになる。したがって,等価インピーダンス\( \ {\dot Z}_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {0}}&=&\frac {\mathrm {j}5\left( 5-\mathrm {j}5\right) }{\mathrm {j}5+\left( 5-\mathrm {j}5\right) } \\[ 5pt ]
&=&\frac {25+\mathrm {j}25}{5} \\[ 5pt ]
&=&5+\mathrm {j}5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:イ
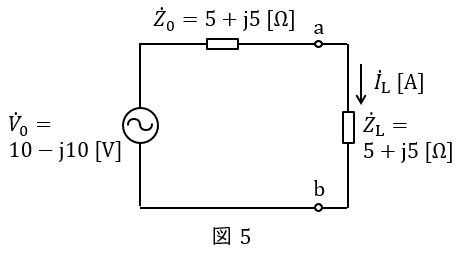
(2)及び(3)より,等価回路は図5のようになる。したがって,負荷\( \ {\dot Z}_{\mathrm {L}} \ \)を流れる電流\( \ {\dot I}_{\mathrm {L}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {L}}&=&\frac {{\dot V}_{\mathrm {0}}}{{\dot Z}_{\mathrm {0}}+{\dot Z}_{\mathrm {L}}} \\[ 5pt ]
&=&\frac {10-\mathrm {j}10}{\left( 5+\mathrm {j}5\right) +\left( 5+\mathrm {j}5\right) } \\[ 5pt ]
&=&\frac {10-\mathrm {j}10}{10+\mathrm {j}10} \\[ 5pt ]
&=&\frac {10-\mathrm {j}10}{10+\mathrm {j}10}\times \frac {10-\mathrm {j}10}{10-\mathrm {j}10} \\[ 5pt ]
&=&\frac {100-\mathrm {j}200-100}{100+100} \\[ 5pt ]
&=&\frac {-\mathrm {j}200}{200} \\[ 5pt ]
&=&-\mathrm {j} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ホ
負荷\( \ {\dot Z}_{\mathrm {L}} \ \)で消費される有効電力\( \ P_{\mathrm {L}} \ \mathrm {[W]} \ \)は,負荷の抵抗分\( \ R_{\mathrm {L}}=5 \ \mathrm {[\Omega ]} \ \)なので,
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&R_{\mathrm {L}}\left| {\dot I}_{\mathrm {L}}\right| ^{2} \\[ 5pt ]
&=&5\times \left| -\mathrm {j}\right| ^{2} \\[ 5pt ]
&=&5\times 1 ^{2} \\[ 5pt ]
&=&5 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは