《理論》〈電気回路〉[R05上:問9]抵抗と誘導性リアクタンスが接続された交流回路の力率に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

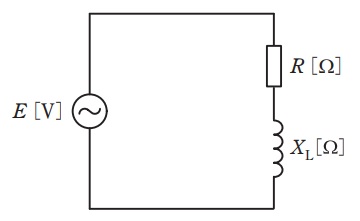
図のように，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)と誘導性リアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)が直列に接続された交流回路がある。\( \ \displaystyle \frac {R}{X_{\mathrm {L}}}=\frac {1}{\sqrt {2}} \ \)の関係があるとき，この回路の力率\( \ \cos \phi \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.43 \ \)　　(2)　\( \ 0.50 \ \)　　(3)　\( \ 0.58 \ \)　　(4)　\( \ 0.71 \ \)　　(5)　\( \ 0.87 \ \)

【ワンポイント解説】

抵抗と誘導性リアクタンスのインピーダンス比が与えられているときの力率を求める問題です。
抵抗とコイル，コンデンサの電圧と電流の関係は交流回路の基本となりますので，必ず理解しておくようにして下さい。
本問は平成14年問6からの再出題となります。

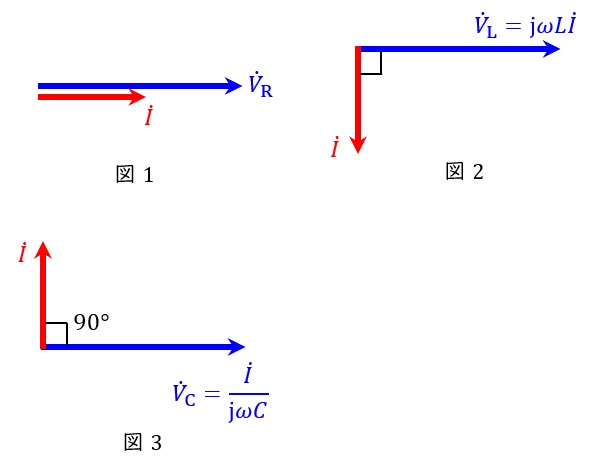
1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
\] となります。この関係をベクトル図に表すと，図1～図3となります。

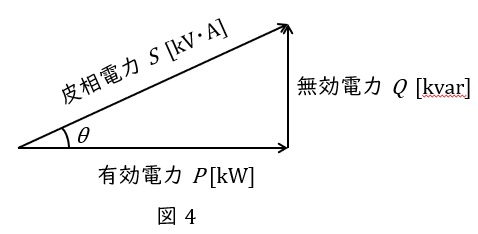
2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図4のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図4において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

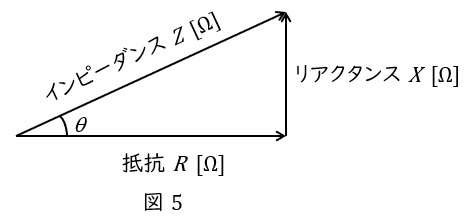
また，線路に電流\( \ I \ \mathrm {[A]} \ \)が流れているとき，皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)，有効電力\( \ P \ \mathrm {[W]} \ \)，無効電力\( \ Q \ \mathrm {[var]} \ \)は，インピーダンスを\( \ Z \ \mathrm {[\Omega ]} \ \)，抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)，リアクタンスを\( \ X \ \mathrm {[\Omega ]} \ \)とすると，
\[
\begin{eqnarray}
S &=&ZI^{2} \\[ 5pt ] P &=&RI^{2} \\[ 5pt ] Q &=&XI^{2} \\[ 5pt ] \end{eqnarray}
\] となるため，\( \ Z \ \mathrm {[\Omega ]} \ \)，\( \ R \ \mathrm {[\Omega ]} \ \)，\( \ X \ \mathrm {[\Omega ]} \ \)に関しても電力と同様な図5のような関係を描くことができます。

【解答】

解答：(3)
ワンポイント解説「2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り，回路の力率\( \ \cos \phi \ \)は，
\[
\begin{eqnarray}
\cos \phi &=&\frac {R}{\sqrt {R^{2}+{X_{\mathrm {L}}}^{2}}} \\[ 5pt ] &=&\frac {R}{\sqrt {R^{2}+\left( \sqrt {2}R\right)^{2}}} \\[ 5pt ] &=&\frac {R}{\sqrt {3R^{2}}} \\[ 5pt ] &=&\frac {R}{\sqrt {3}R} \\[ 5pt ] &=&\frac {1}{\sqrt {3}} \\[ 5pt ] &≒&0.58 \\[ 5pt ] \end{eqnarray}
\] と求められる。