《理論》〈電子理論〉[R05:問7]MOSFET を用いた回路に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，$ \ \mathrm {MOSFET} \ $を用いた回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

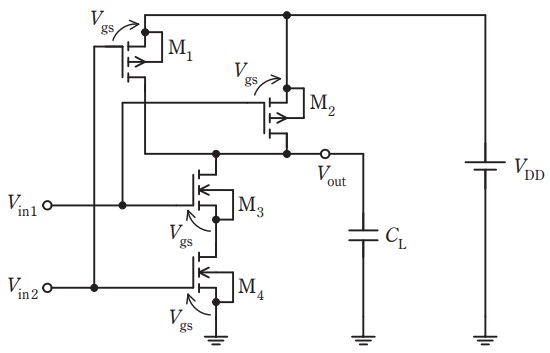
図に$ \ \mathrm {n} \ $チャネル$ \ \mathrm {MOSFET} \ $及び$ \ \mathrm {p} \ $チャネル$ \ \mathrm {MOSFET} \ $からなる回路を示す。本問では，$ \ \mathrm {MOSFET} \ $のゲート－ソース間電圧$ \ V_{\mathrm {gs}} \ \mathrm {[V]} \ $は図中に示す向きを正とし，$ \ \mathrm {n} \ $チャネル$ \ \mathrm {MOSFET} \ $及び$ \ \mathrm {p} \ $チャネル$ \ \mathrm {MOSFET} \ $はいずれも$ \ V_{\mathrm {gs}} \ $により制御される理想的なスイッチとみなせるとする。$ \ V_{\mathrm {gs}}＞V_{\mathrm {T}} \ $を満たすときにスイッチは導通し，ドレイン－ソース間は短絡（ショート）となる。一方，$ \ V_{\mathrm {gs}}≦V_{\mathrm {T}} \ $のときスイッチは非導通となり，ドレイン－ソース間は開放（オープン）になる。ただし，$ \ V_{\mathrm {T}} \ \mathrm {[V]} \ $は正の定数であり，電源電圧$ \ V_{\mathrm {DD}} \ \mathrm {[V]} \ $は$ \ V_{\mathrm {T}} \ $より十分に大きいとする。また，回路には$ \ C_{\mathrm {L}} \ \mathrm {[F]} \ $の負荷容量が接続されている。

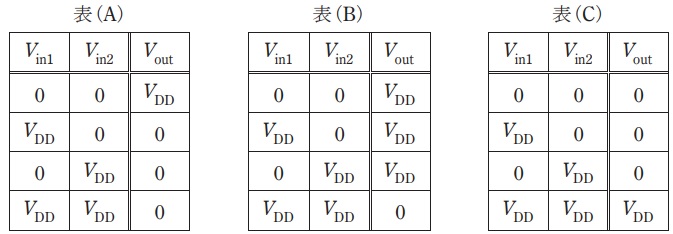
まず，図の回路に入力電圧として$ \ V_{\mathrm {in1}} \ $と$ \ V_{\mathrm {in2}} \ $のいずれにも$ \ 0 \ \mathrm {V} \ $を加える。このとき各$ \ \mathrm {MOSFET} \ $の状態は$ \ \fbox {　（１）　} \ $となるため，出力電圧$ \ V_{\mathrm {out}} \ \mathrm {[V]} \ $は$ \ \fbox {　（２）　} \ $となる。次に，$ \ V_{\mathrm {in1}} \ $と$ \ V_{\mathrm {in2}} \ $を$ \ V_{\mathrm {DD}} \ $又は$ \ 0 \ \mathrm {V} \ $として回路の入出力電圧の関係を調べると，表$ \ \fbox {　（３）　} \ $が得られる。$ \ V_{\mathrm {DD}} \ $に$ \ 1 \ $（真），$ \ 0 \ \mathrm {V} \ $に$ \ 0 \ $（偽）をそれぞれ割り当てると，回路の出力の論理式は$ \ \fbox {　（４）　} \ $となる。

図の回路にはいずれの状態でも定常的な電流は流れない。回路には負荷容量$ \ C_{\mathrm {L}} \ $を充放電する電流のみが流れる。回路の出力が$ \ 0 \ \mathrm {V} \ $と$ \ V_{\mathrm {DD}} \ $を$ \ f \ \mathrm {[Hz]} \ $で繰り返しているとき，電源から回路に流れ込む平均電流は$ \ \fbox {　（５）　} \ \mathrm {[A]} \ $となる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　V_{\mathrm {in1}}\cdot V_{\mathrm {in2}}　　　　　&（ロ）&　0　　　　　&（ハ）&　\frac {1}{2}C_{\mathrm {L}}{V_{\mathrm {DD}}}^{2} \\[ 5pt ] &（ニ）&　\overline {V_{\mathrm {in1}}+ V_{\mathrm {in2}}}　　　　　&（ホ）&　fC_{\mathrm {L}}V_{\mathrm {DD}}　　　　　&（ヘ）&　\overline {V_{\mathrm {in1}}\cdot V_{\mathrm {in2}}} \\[ 5pt ] &（ト）&　V_{\mathrm {DD}}　　　　　&（チ）&　\frac {V_{\mathrm {DD}}}{2}　　　　　&（リ）&　fC_{\mathrm {L}}{V_{\mathrm {DD}}}^{2} \\[ 5pt ] &（ヌ）&　\left( \mathrm {A} \right)　　　　　&（ル）&　\left( \mathrm {B} \right)　　　　　&（ヲ）&　\left( \mathrm {C} \right) \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ワ）&　\mathrm {M} _{1} \ と \ \mathrm {M} _{2} \ がオンとなり \ \mathrm {M} _{3} \ と \ \mathrm {M} _{4} \ がオフ \\[ 5pt ] &（カ）&　\mathrm {M} _{1} \ と \ \mathrm {M} _{3} \ がオンとなり \ \mathrm {M} _{2} \ と \ \mathrm {M} _{4} \ がオフ \\[ 5pt ] &（ヨ）&　\mathrm {M} _{3} \ と \ \mathrm {M} _{4} \ がオンとなり \ \mathrm {M} _{1} \ と \ \mathrm {M} _{2} \ がオフ \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電子回路とブール代数を組み合わせた問題です。
機械科目のパワーエレクトロニクスや情報の内容を組み合わせたやや複合的な問題となっています。文章読解も必要となるため落ち着いて解く必要があります。

1.ブール代数における論理積，論理和，否定
ブール代数における論理積，論理和，否定はベン図を組み合わせると理解しやすいです。

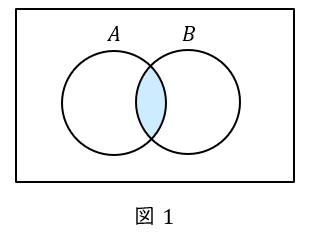
①論理積$ \ \left( \mathrm {AND} \right) \ $
　$ \ A \ $かつ$ \ B \ $の条件を満たすものを$ \ A\cdot B \ $で表し，ベン図で表すと図1のようになります。

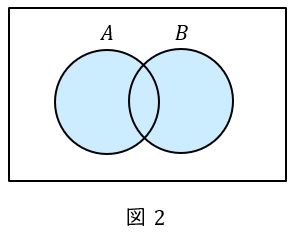
②論理和$ \ \left( \mathrm {OR} \right) \ $
　$ \ A \ $または$ \ B \ $の条件を満たすものを$ \ A+B \ $で表し，ベン図で表すと図2のようになります。

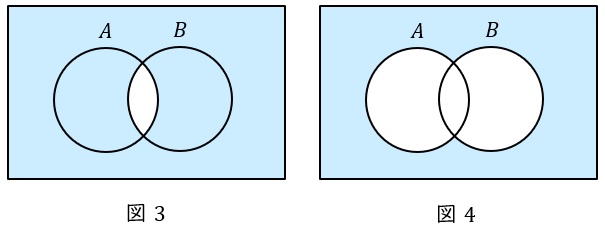
③否定$ \ \left( \mathrm {NOT} \right) \ $
　条件を満たさないものを表し，論理積$ \ A\cdot B \ $の否定は$ \ \overline {A\cdot B} \ $でベン図で表すと図3，論理和$ \ A+B \ $の否定は$ \ \overline {A+B} \ $でベン図で表すと図4のようになります。

【解答】

(1)解答：ワ
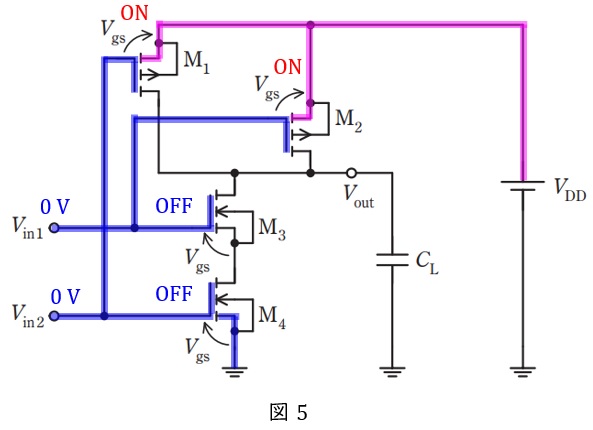
$ \ V_{\mathrm {in1}} \ $と$ \ V_{\mathrm {in2}} \ $のいずれにも$ \ 0 \ \mathrm {V} \ $を加えたとき，各$ \ \mathrm {MOSFET} \ $に加わる電圧は図5のようになる。
したがって，$ \ V_{\mathrm {gs}}＞V_{\mathrm {T}} \ $となり，オンとなる$ \ \mathrm {MOSFET} \ $は$ \ \mathrm {M} _{1} \ $と$ \ \mathrm {M} _{2} \ $，$ \ V_{\mathrm {gs}}≦V_{\mathrm {T}} \ $となり，オフとなる$ \ \mathrm {MOSFET} \ $は$ \ \mathrm {M} _{3} \ $と$ \ \mathrm {M} _{4} \ $と求められる。

(2)解答：ト
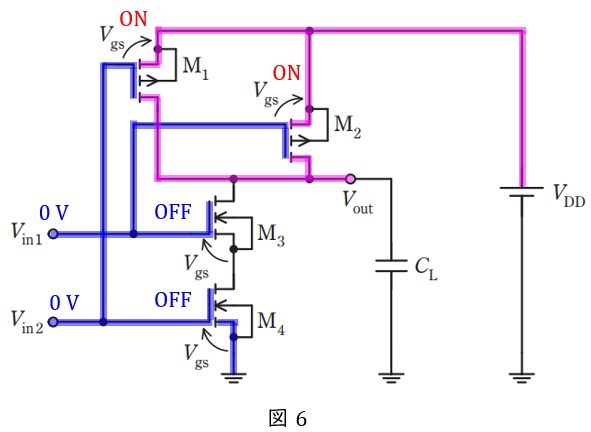
題意より，$ \ \mathrm {MOSFET} \ $がオンのときドレイン－ソース間は短絡（ショート)となり，$ \ \mathrm {MOSFET} \ $がオフのときドレイン－ソース間は開放(オープン)となるので，$ \ \mathrm {M} _{1} \ $と$ \ \mathrm {M} _{2} \ $は短絡，$ \ \mathrm {M} _{3} \ $と$ \ \mathrm {M} _{4} \ $は開放と考えれば良い。
したがって，図6に示すように$ \ \mathrm {M} _{1} \ $と$ \ \mathrm {M} _{2} \ $が導通するため，出力電圧$ \ V_{\mathrm {out}} \ \mathrm {[V]} \ $は$ \ V_{\mathrm {DD}} \ \mathrm {[V]} \ $となる。

(3)解答：ル
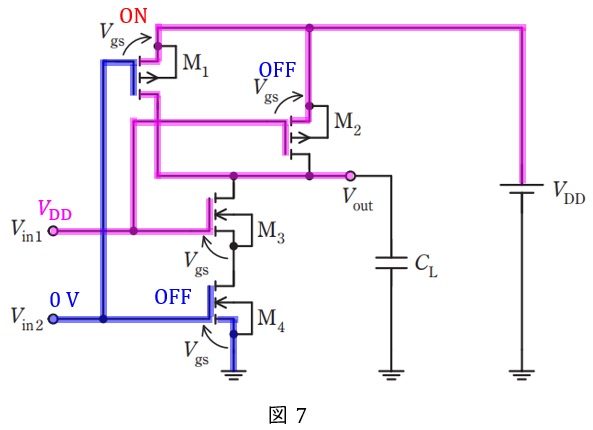
(2)と同様，回路の入出力電圧を考えると，
$ \ V_{\mathrm {in1}} \ $が$ \ V_{\mathrm {DD}} \ \mathrm {[V]} \ $，$ \ V_{\mathrm {in2}} \ $が$ \ 0 \ \mathrm {V} \ $のとき図7のようになり$ \ V_{\mathrm {out}} \ \mathrm {[V]} \ $は$ \ V_{\mathrm {DD}} \ \mathrm {[V]} \ $
$ \ V_{\mathrm {in1}} \ $が$ \ 0 \ \mathrm {V} \ $，$ \ V_{\mathrm {in2}} \ $が$ \ V_{\mathrm {DD}} \ \mathrm {[V]} \ $のとき図8のようになり$ \ V_{\mathrm {out}} \ \mathrm {[V]} \ $は$ \ V_{\mathrm {DD}} \ \mathrm {[V]} \ $
$ \ V_{\mathrm {in1}} \ $と$ \ V_{\mathrm {in2}} \ $がともに$ \ V_{\mathrm {DD}} \ \mathrm {[V]} \ $のとき図9のようになり$ \ V_{\mathrm {out}} \ \mathrm {[V]} \ $は$ \ 0 \ \mathrm {V} \ $
となるため，真理値表は$ \ \left( \mathrm {B} \right) \ $と求められる。

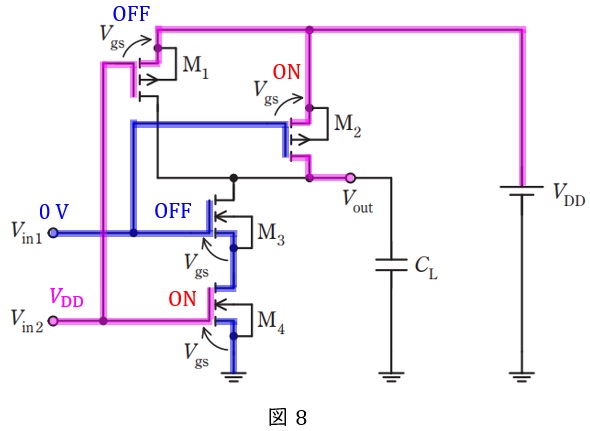
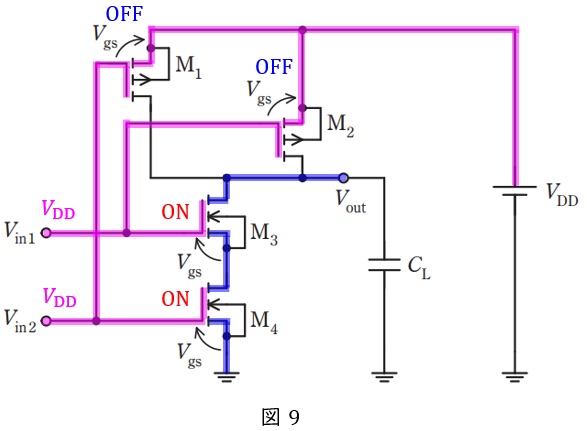
(4)解答：ヘ
$ \ V_{\mathrm {DD}} \ $に$ \ 1 \ $(真)，$ \ 0 \ \mathrm {V} \ $に$ \ 0 \ $(偽)をそれぞれ割り当てると，出力は入力がともに$ \ 1 \ $のとき$ \ 0 \ $となるため，$ \ \overline {V_{\mathrm {in1}}\cdot V_{\mathrm {in2}}} \ $と求められる。

(5)解答：ホ
問題文より，定常的な電流は流れないので，回路の出力が$ \ 0 \ \mathrm {V} \ $と$ \ V_{\mathrm {DD}} \ $の１回で充放電する電荷量は$ \ C_{\mathrm {L}}V_{\mathrm {DD}} \ $であり，これが$ \ 1 \ $秒間に$ \ f \ $回繰り返される$ \ \left( =f \ \mathrm {[Hz]}\right) \ $ので，$ \ 1 \ $秒間に電源から流れ込む電荷量（＝電流）は$ \ fC_{\mathrm {L}}V_{\mathrm {DD}} \ \mathrm {[A]} \ $と求められる。