Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は理想変成器を含む交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
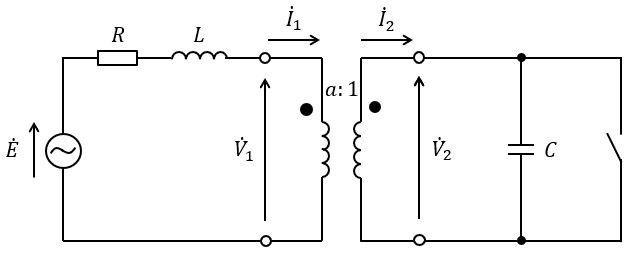
図のように,電圧\( \ \dot E \ \),角周波数\( \ \omega \ \)の正弦波交流電源に抵抗値\( \ R \ \)の抵抗,インダクタンス\( \ L \ \)のコイル,巻数比\( \ a:1 \ \)の理想変成器,静電容量\( \ C \ \)のコンデンサとスイッチが接続されている。理想変成器の一次側,二次側の電圧,電流の関係は次のとおりである。
\[
\begin{eqnarray}
\begin{bmatrix}
{\dot V}_{1} \\
{\dot I}_{1}
\end{bmatrix} &=& \begin{bmatrix}
a & 0 \\
0 & \displaystyle \frac {1}{a}
\end{bmatrix}\begin{bmatrix}
{\dot V}_{2} \\
{\dot I}_{2}
\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
(a) 回路のスイッチが開いているとき,理想変成器の一次側の電流\( \ {\dot I}_{1} \ \)は\( \ {\dot I}_{1}=\fbox { (1) } \ \)となる。電流\( \ {\dot I}_{1} \ \)が電源電圧\( \ \dot E \ \)と同相となるのは巻数比\( \ a \ \)が\( \ a= \ \fbox { (2) } \ \)のときである。このとき理想変成器の一次側の電圧\( \ {\dot V}_{1} \ \)が\( \ \left| {\dot V}_{1}\right| =\left| \dot E\right| \ \)となる角周波数\( \ \omega \ \)は\( \ \omega = \ \fbox { (3) } \ \)である。
(b) 回路のスイッチが閉じているとき,理想変成器の一次側の電流\( \ {\dot I}_{1} \ \)は\( \ {\dot I}_{1}= \ \fbox { (4) } \ \)となる。このときの回路の消費電力を\( \ P \ \)とすると\( \ P= \ \fbox { (5) } \ \)となる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\dot E}{\sqrt {R^{2}+\omega ^{2}L^{2}}} &(ロ)& \frac {\dot Ea}{R+\mathrm {j}\omega L+\displaystyle \frac {a}{\mathrm {j}\omega C}} &(ハ)& \frac {\dot E}{R} \\[ 5pt ]
&(ニ)& \frac {\dot Ea^{2}}{R+\mathrm {j}\omega L+\displaystyle \frac {a^{2}}{\mathrm {j}\omega C}} &(ホ)& \omega \sqrt {LC} &(ヘ)& \frac {\dot E}{R+\mathrm {j}\omega L+\displaystyle \frac {a^{2}}{\mathrm {j}\omega C}} \\[ 5pt ]
&(ト)& \omega ^{2}LC &(チ)& \frac {1}{CR} &(リ)& \frac {R}{L} \\[ 5pt ]
&(ヌ)& \frac {1}{\omega \sqrt {LC}} &(ル)& \frac {\left| \dot E\right| ^{2}\omega L}{R^{2}+\omega ^{2}L^{2}} &(ヲ)& \frac {\left| \dot E\right| ^{2}R}{R^{2}+\omega ^{2}L^{2}} \\[ 5pt ]
&(ワ)& \frac {1}{LC} &(カ)& \frac {\left| \dot E\right| ^{2}}{R} &(ヨ)& \frac {\dot E}{R+\mathrm {j}\omega L} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
理想変成器を含む交流回路の計算問題です。
一般的に電力科目や機械科目で出題される変圧比の関係を理論科目に持ってきた点が\( \ 3 \ \)種よりも難易度が高いポイントかと思います。やや面倒でも図4や図5のようにきちんと回路を描くと間違えにくくなりますので,ぜひ取り入れるようにして下さい。
1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンスは,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,それぞれの電圧と電流の関係は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ]
{\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ]
{\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ]
\end{eqnarray}
\]
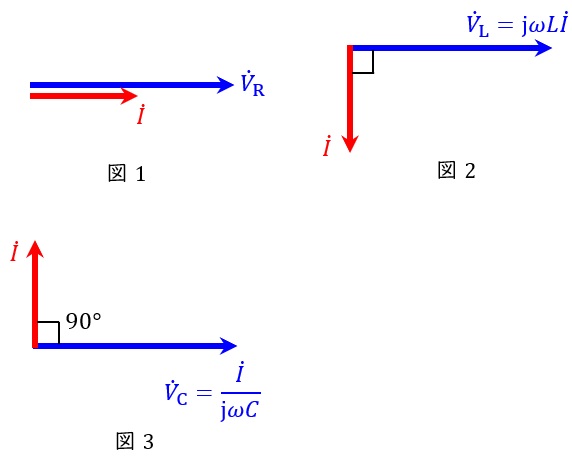
となります。この関係をベクトル図に表すと,図1~図3となります。
2.変圧器の巻数比と変圧比,変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \),電圧\( \ V_{1} \ \mathrm {[V]} \ \),電流\( \ I_{1} \ \mathrm {[A]} \ \),二次側の巻数\( \ N_{2} \ \),電圧\( \ V_{2} \ \mathrm {[V]} \ \),電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると,巻数比\( \ \displaystyle a=\frac {N_{1}}{N_{2}} \ \)は,
\[
\begin{eqnarray}
a&=&\frac {N_{1}}{N_{2}} =\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となります。インピーダンスは電圧を電流で割ったものであるため,一次側換算のインピーダンス\( \ Z_{1} \ \mathrm {[\Omega ]} \ \),二次側換算のインピーダンス\( \ Z_{2} \ \mathrm {[\Omega ]} \ \)とすると,
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{2}} &=&\frac {\displaystyle \frac {V_{1}}{I_{1}}}{\displaystyle \frac {V_{2}}{I_{2}}} \\[ 5pt ]
&=&\frac {V_{1}}{I_{1}}\times \frac {I_{2}}{V_{2}} \\[ 5pt ]
&=&\frac {V_{1}}{V_{2}}\times \frac {I_{2}}{I_{1}} \\[ 5pt ]
&=&\left( \frac {N_{1}}{N_{2}} \right) ^{2} \\[ 5pt ]
&=&a^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ヘ
インダクタンス\( \ L \ \)と静電容量\( \ C \ \)のリアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)と\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」の通り,
\[
\begin{eqnarray}
X_{\mathrm {L}}&=&\omega L \\[ 5pt ]
X_{\mathrm {C}}&=&\frac {1}{\omega C} \\[ 5pt ]
\end{eqnarray}
\]
であり,コンデンサのリアクタンスを一次側に換算した値\( \ {X_{\mathrm {C}}}^{\prime } \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「2.変圧器の巻数比と変圧比,変流比の関係」の通り,
\[
\begin{eqnarray}
{X_{\mathrm {C}}}^{\prime }&=&\frac {a^{2}}{\omega C} \\[ 5pt ]
\end{eqnarray}
\]
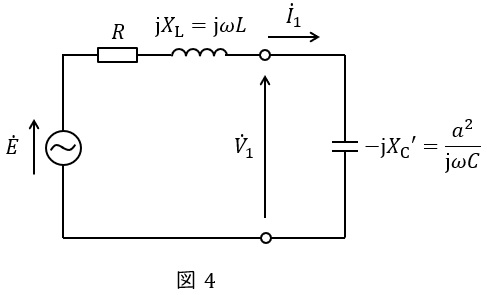
となるので,スイッチが開いているときの一次側換算した回路は図4のようになる。したがって,変成器の一次側の電流\( \ {\dot I}_{1} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{1}&=&\frac {\dot E}{R+\mathrm {j}X_{\mathrm {L}}-\mathrm {j}X_{\mathrm {C}}} \\[ 5pt ]
&=&\frac {\dot E}{R+\mathrm {j}\omega L+\displaystyle \frac {a^{2}}{\mathrm {j}\omega C}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ホ
(1)解答式より,電圧と電流が同相となるのは,回路のリアクタンスが零となるとき,すなわち\( \ X_{\mathrm {L}}={X_{\mathrm {C}}}^{\prime } \ \)となるときであるから,
\[
\begin{eqnarray}
\omega L&=&\frac {a^{2}}{\omega C} \\[ 5pt ]
a^{2}&=&\omega ^{2}LC \\[ 5pt ]
a&=&\omega \sqrt {LC} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
(1)解答式より,変成器の一次側の電圧\( \ {\dot V}_{1} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{1}&=&-\mathrm {j}{X_{\mathrm {C}}}^{\prime }{\dot I}_{1} \\[ 5pt ]
&=&\frac {a^{2}}{\mathrm {j}\omega C}\frac {\dot E}{R+\mathrm {j}\omega L+\displaystyle \frac {a^{2}}{\mathrm {j}\omega C}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {a^{2}}{\mathrm {j}\omega C}}{R+\mathrm {j}\left( \omega L-\displaystyle \frac {a^{2}}{\omega C}\right) }\dot E \\[ 5pt ]
\end{eqnarray}
\]
であり,(2)解答式の条件より,
\[
\begin{eqnarray}
{\dot V}_{1}&=&\frac {\displaystyle \frac {\omega ^{2}LC}{\mathrm {j}\omega C}}{R+\mathrm {j}\left( \omega L-\displaystyle \frac {\omega ^{2}LC}{\omega C}\right) }\dot E \\[ 5pt ]
&=&\frac {\displaystyle \frac {\omega L}{\mathrm {j}}}{R+\mathrm {j}\left( \omega L-\omega L\right) }\dot E \\[ 5pt ]
&=&\frac {\omega L}{\mathrm {j}R}\dot E \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,その大きさ\( \ \left| {\dot V}_{1}\right| \ \)は,
\[
\begin{eqnarray}
\left| {\dot V}_{1}\right| &=&\frac {\omega L}{R}\left| \dot E\right| \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より\( \ \left| {\dot V}_{1}\right| =\left| \dot E\right| \ \)であるから,
\[
\begin{eqnarray}
\left| \dot E\right| &=&\frac {\omega L}{R}\left| \dot E\right| \\[ 5pt ]
1 &=&\frac {\omega L}{R} \\[ 5pt ]
\omega &=&\frac {R}{L} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
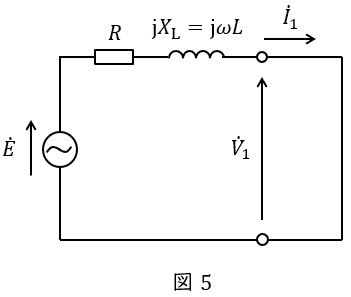
スイッチを閉じたとき,コンデンサは短絡されているので,回路は図5のようになる。したがって,変成器の一次側の電流\( \ {\dot I}_{1} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{1}&=&\frac {\dot E}{R+\mathrm {j}X_{\mathrm {L}}} \\[ 5pt ]
&=&\frac {\dot E}{R+\mathrm {j}\omega L} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
(4)解答式より,電流\( \ {\dot I}_{1} \ \)の大きさ\( \ \left| {\dot I}_{1}\right| \ \)は,
\[
\begin{eqnarray}
\left| {\dot I}_{1}\right| &=&\frac {\left| \dot E\right| }{\sqrt {R^{2}+\left( \omega L\right) ^{2}}} \\[ 5pt ]
&=&\frac {\left| \dot E\right| }{\sqrt {R^{2}+\omega ^{2}L^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,回路の消費電力\( \ P \ \)は,
\[
\begin{eqnarray}
P &=&R\left| {\dot I}_{1}\right| ^{2} \\[ 5pt ]
&=&\frac {\left| \dot E\right| ^{2}R}{R^{2}+\omega ^{2}L^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは