Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,半導体中の電界による電気伝導に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお,半導体中の正孔の電荷量を\( \ e \ ( > 0 ) \ \),有効質量を\( \ m_{\mathrm {h}} \ \)とし,有効質量の変化は無視できるものとする。
\( \ \mathrm {p} \ \)形半導体中に一定の電界\( \ E \ \)が一様に印加されているとき,一つの正孔は電界から力\( \ F_{1}= \ \fbox { (1) } \ \)を受けて運動する。その速度を\( \ v \ \)とする。一方,半導体中で運動する正孔は,格子振動などによる散乱を受け,速度\( \ v \ \)に比例する大きさで,\( \ v \ \)を減速させる向きの力\( \ F_{2} \ \)を受ける。その比例定数を\( \ \displaystyle \frac {m_{\mathrm {h}}}{\tau } \ \)と仮定すると,\( \ F_{2}= \ \fbox { (2) } \ \)と表される。なお,\( \ \tau \ \)は,正孔が散乱を受けるまでの時間の目安となる定数である。\( \ F_{1} \ \)と\( \ F_{2} \ \)が釣り合うと速度\( \ v \ \)は一定となり,その大きさは\( \ v= \ \fbox { (3) } \ \cdot E \ \)と表される。この\( \ v \ \)をドリフト速度と呼び,\( \ \fbox { (3) } \ \)は,\( \ \fbox { (4) } \ \)と呼ばれる。\( \ v \ \)が一定である場合は正孔の運動エネルギーは変化しないが,一方で,正孔は電界から常に仕事をされている。すなわち,電界から力\( \ F_{1} \ \)を受けて距離\( \ \mathit {\Delta } x \ \)移動する際に正孔が電界から受け取るエネルギーは\( \ F_{1}\cdot \mathit {\Delta } x \ \)であり,単位時間当たりに受け取るエネルギー\( \ P \ \)は,\( \ \mathit {\Delta }x \ \)進むのに必要な時間\( \ \mathit {\Delta }t \ \)で除すことにより,\( \ \displaystyle P=F_{1}\cdot \frac {\mathit {\Delta } x}{\mathit {\Delta } t} \ \)である。これを\( \ e \ \),\( \ \tau \ \),\( \ m_{\mathrm {h}} \ \),\( \ E \ \)を用いて表すと,\( \ P= \ \fbox { (5) } \ \)となる。\( \ P \ \)は正孔一つ当たりのジュール損失に相当する。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& フェルミ準位 &(ロ)& 拡散定数 &(ハ)& 移動度 \\[ 5pt ]
&(ニ)& \frac {m_{\mathrm {h}}}{e^{2}\tau }E^{2} &(ホ)& \frac {e^{2}\tau }{m_{\mathrm {h}}}E^{2} &(ヘ)& \frac {m_{\mathrm {h}}}{v\tau } \\[ 5pt ]
&(ト)& \frac {e}{E} &(チ)& \frac {m_{\mathrm {h}}}{e\tau } &(リ)& \frac {e\tau }{m_{\mathrm {h}}} \\[ 5pt ]
&(ヌ)& eE &(ル)& \frac {vm_{\mathrm {h}}}{\tau } &(ヲ)& \frac {e\tau ^{2}}{m_{\mathrm {h}}}E^{2} \\[ 5pt ]
&(ワ)& \frac {E}{e} &(カ)& \frac {\tau }{em_{\mathrm {h}}} &(ヨ)& \frac {v\tau }{m_{\mathrm {h}}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
半導体中におけるキャリヤが電界から受ける力と速度に関する問題です。
電子や正孔が電界から受ける力を基本としながら,文章を読解し解いていく問題です。
その場で考えながら解いていく問題は得意不得意がすごく分かれますが,きちんと読解すれば計算量も多くない問題も多いため,是非問題慣れするようにして下さい。
1.一様電界中において電子に働く力と電子の持つエネルギー
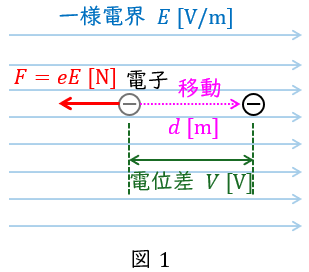
図1に示すように,一様な電界\( \ E \ \mathrm {[V/m]} \ \)中に電子\( \ -e \ \mathrm {[C]} \ \)があるとき,この電子に働く力の大きさ\( \ F \ \mathrm {[N]} \ \)は,
\[
\begin{eqnarray}
F &=&eE \\[ 5pt ]
\end{eqnarray}
\]
で向きは電界の向きと逆向きとなります。この電子を力の向きに逆らって\( \ d \ \mathrm {[m]} \ \)移動させるのに必要な仕事\( \ W \ \mathrm {[J]} \ \)は,
\[
\begin{eqnarray}
W &=&Fd \\[ 5pt ]
&=&eEd \\[ 5pt ]
\end{eqnarray}
\]
であり,電界\( \ E \ \mathrm {[V/m]} \ \)と電位差\( \ V \ \mathrm {[V]} \ \)の関係\( \ V=Ed \ \)より,
\[
\begin{eqnarray}
W &=&eV \\[ 5pt ]
\end{eqnarray}
\]
となります。これは,外力により電子に蓄えられた位置エネルギーと言えます。
2.キャリヤの移動度\( \ \mu \ \)
電界\( \ E \ \mathrm {[V / m]} \ \)が加わっている電界中に正孔や電子等のキャリヤがあるとすると,キャリヤは電界\( \ E \ \mathrm {[V / m]} \ \)に比例した速度で動きます。その時のキャリヤの速度\( \ v \ \mathrm {[m / s]} \ \)は,比例定数(移動度)を\( \ \mu \ \mathrm {[m^{2} / V\cdot s]} \ \)とすると,
\[
\begin{eqnarray}
v &=&\mu E \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:ヌ
ワンポイント解説「1.一様電界中において電子に働く力と電子の持つエネルギー」の通り,電荷\( \ e \ \)の正孔が電界\( \ E \ \)から受ける力\( \ F_{1} \ \)は,
\[
\begin{eqnarray}
F_{1} &=&eE \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ル
題意より,正孔は比例定数\( \ \displaystyle \frac {m_{\mathrm {h}}}{\tau } \ \)で速度\( \ v \ \)に比例する大きさの力\( \ F_{2} \ \)を受けるとなっているので,
\[
\begin{eqnarray}
F_{2} &=&\frac {m_{\mathrm {h}}}{\tau }v \\[ 5pt ]
&=&\frac {vm_{\mathrm {h}}}{\tau } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
題意より,\( \ F_{1}=F_{2} \ \)であるから,
\[
\begin{eqnarray}
eE &=& \frac {vm_{\mathrm {h}}}{\tau } \\[ 5pt ]
v &=& \frac {e\tau }{m_{\mathrm {h}}}E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
題意より解答候補は,(イ)フェルミ準位,(ロ)拡散定数,(ハ)移動度,になると思います。
ワンポイント解説「2.キャリヤの移動度\( \ \mu \ \)」の通り,キャリヤの速度\( \ v \ \)と電界\( \ E \ \)との比例定数を移動度といいます。
(5)解答:ホ
ワンポイント解説「1.一様電界中において電子に働く力と電子の持つエネルギー」及び\( \ \displaystyle P=F_{1}\cdot \frac {\mathit {\Delta } x}{\mathit {\Delta } t}=F_{1}v \ \)より,
\[
\begin{eqnarray}
P &=& eE\cdot \frac {e\tau }{m_{\mathrm {h}}}E \\[ 5pt ]
&=& \frac {e^{2}\tau }{m_{\mathrm {h}}}E^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは