《理論》〈電磁気〉[R06上:問1]誘電体を挿入した平行平板コンデンサ内の等電位線の分布に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

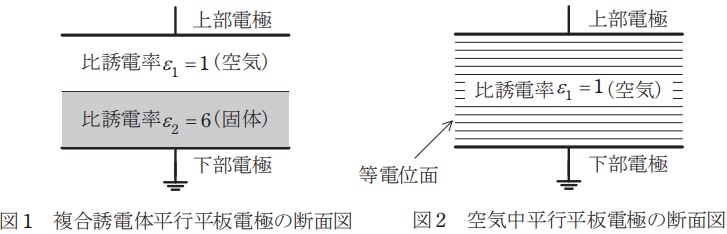
図1に示すような，空気を含む二つの誘電体からなる平行平板電極がある。この下部電極を接地し，上部電極に電圧を加えたときの電極間の等電位線の分布を示す断面図として，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，誘電体の導電性及び電極と誘電体の端効果は無視できるものとする。

参考までに固体誘電体を取り除いた，空気中平行平板電極の場合の等電位線の分布を図2に示す。

【ワンポイント解説】

平行平板コンデンサ内の等電位線を求める問題です。
平行平板コンデンサ内の電界の割合を考える必要がる場合，電束密度が一定であることを利用すると問題なく解ける問題が多いです。
本問は平成18年問2からの再出題となります。

1.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \mathrm {[m]} \ \)の平行平板コンデンサに電圧\( \ V \ \mathrm {[V]} \ \)をかけると，極板間の電界\( \ E \ \mathrm {[V / m]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

2.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係
極板間の誘電率を\( \ \varepsilon \ \mathrm {[F / m]} \ \)とすると，電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)と電界\( \ E \ \mathrm {[V / m]} \ \)には，
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ] \end{eqnarray}
\] の関係があります。真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)，誘電体の比誘電率を\( \ \varepsilon _{\mathrm {r}} \ \)とすると，\( \ \varepsilon = \varepsilon _{\mathrm {r}}\varepsilon _{0} \ \)の関係があるので，
\[
\begin{eqnarray}
D&=&\varepsilon _{\mathrm {r}}\varepsilon _{0}E \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
平行平板コンデンサ内の電束密度を\( \ D \ \mathrm {[C / m^{2}]} \ \)とすると，空気中の電界\( \ E_{1} \ \mathrm {[V / m]} \ \)及び誘電体中の電界\( \ E_{2} \ \mathrm {[V / m]} \ \)は，ワンポイント解説「2.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係」の通り，
\[
\begin{eqnarray}
E_{1}&=&\frac {D}{\varepsilon _{\mathrm {r1}}\varepsilon _{0}} \\[ 5pt ] &=&\frac {D}{\varepsilon _{0}} \\[ 5pt ] E_{2}&=&\frac {D}{\varepsilon _{\mathrm {r2}}\varepsilon _{0}} \\[ 5pt ] &=&\frac {D}{6\varepsilon _{0}} \\[ 5pt ] &=&\frac {E_{1}}{6} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「1.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係」の通り，平行平板コンデンサ内の電圧\( \ V \ \)は電界\( \ E \ \)に比例して変化していくので，誘電体中の電圧降下は空気中の電圧降下の\( \ \displaystyle \frac {1}{6} \ \)倍となる。したがって，等電位面の分布は誘電体の方が本数が少ない(5)と求められる。