《電力》〈配電〉[H18:問16]配電線の電圧降下と負荷電力の関係に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

三相\( \ 3 \ \)線式\( \ 1 \ \)回線の専用配電線がある。変電所の送り出し電圧が\( \ 6 \ 600 \ \mathrm {[V]} \ \)，末端にある負荷の端子電圧が\( \ 6 \ 450 \ \mathrm {[V]} \ \)，力率が遅れの\( \ 70 \ [％] \ \)であるとき，次の(a)及び(b)に答えよ。

ただし， 電線\( \ 1 \ \)線当たりの抵抗は\( \ 0.45 \ \mathrm {[\Omega / km]} \ \)，リアクタンスは\( \ 0.35 \ \mathrm {[\Omega / km]} \ \)，線路のこう長は\( \ 5 \ \mathrm {[km]} \ \)とする。

(a)　この負荷に供給される電力\( \ W_{1} \ \mathrm {[kW]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 180 \ \)　　(2)　\( \ 200 \ \)　　(3)　\( \ 220 \ \)　　(4)　\( \ 240 \ \)　　(5)　\( \ 260 \ \)

(b)　負荷が遅れ力率\( \ 80 \ [％] \ \)，\( \ W_{2} \ \mathrm {[kW]} \ \)に変化したが線路損失は変わらなかった。\( \ W_{2} \ \mathrm {[kW]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 254 \ \)　　(2)　\( \ 274 \ \)　　(3)　\( \ 294 \ \)　　(4)　\( \ 314 \ \)　　(5)　\( \ 334 \ \)

【ワンポイント解説】

配電線の電圧降下と力率から負荷電力を求める問題です。
どこから手を付けたら良いか迷う問題かと思いますが，その場合には求められるものをどんどん求めていけば道筋が見えてくるかと思います。
まずはすぐに計算できそうな配電線のインピーダンスや無効率\( \ \sin \theta \ \)から求めるようにして下さい。

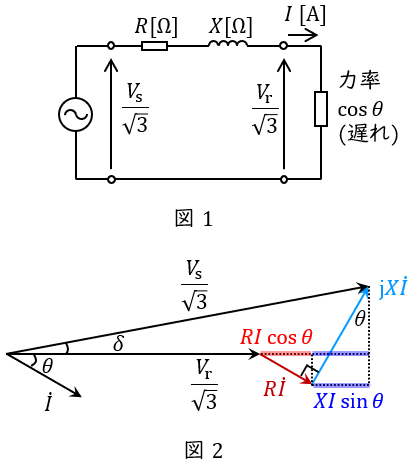
1.三相\( \ 3 \ \)線式送電線の電圧降下の近似式
三相回路においては，一相分の等価回路及びベクトル図は図1及び図2のように描くことができ，送電端電圧と受電端電圧の位相差\( \ \delta \ \mathrm {[rad]} \ \)が無視できるぐらい小さいとしたときの電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
\frac {V_{\mathrm {s}}}{\sqrt {3}}&≃&\frac {V_{\mathrm {r}}}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ] \frac {V_{\mathrm {s}}}{\sqrt {3}}-\frac {V_{\mathrm {r}}}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ] V_{\mathrm {s}}-V_{\mathrm {r}}&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ] \varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

(a)解答：(4)
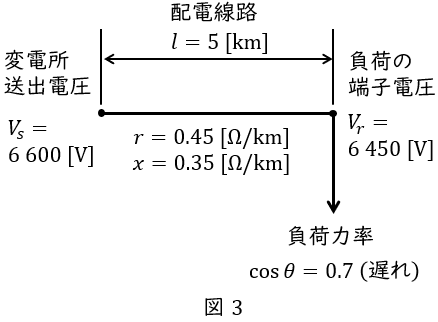
題意に沿って図を描くと図3のようになる。
配電線\( \ 1 \ \)線当たりの抵抗\( \ R \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R &=&rl \\[ 5pt ] &=&0.45\times 5 \\[ 5pt ] &=&2.25 \ \mathrm {[\Omega ]} \\[ 5pt ] X &=&xl \\[ 5pt ] &=&0.35\times 5 \\[ 5pt ] &=&1.75 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，負荷の\( \ \sin \theta \ \)は，
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\sqrt {1-0.7 ^{2} } \\[ 5pt ] &≒&0.714 \ 1 \\[ 5pt ] \end{eqnarray}
\] となる。電圧降下の近似式より，配電線に流れる電流\( \ I \ \mathrm {[A]} \ \)は，ワンポイント解説「1.三相\( \ 3 \ \)線式送電線の電圧降下の近似式」の通り，
\[
\begin{eqnarray}
V_{s}-V_{r}&=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] I&=&\frac {V_{s}-V_{r}}{\sqrt {3}\left( R\cos \theta +X\sin \theta \right) } \\[ 5pt ] &=&\frac {6 \ 600-6 \ 450}{\sqrt {3}\times \left( 2.25\times 0.7 +1.75\times 0.714 \ 1 \right) } \\[ 5pt ] &≒&30.66 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，負荷に供給される電力\( \ W_{1} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
W_{1}&=&\sqrt {3}V_{r}I\cos \theta \\[ 5pt ] &=&\sqrt {3}\times 6 \ 450 \times 30.66 \times 0.7 \\[ 5pt ] &≒&239 \ 800 \ \mathrm {[W]}　→　240 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

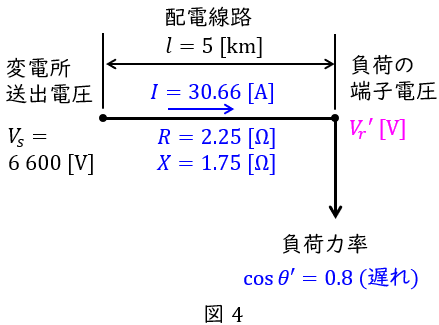
(b)解答：(2)
負荷の力率が\( \ \cos \theta ^{\prime }=0.8 \ \)になったときの単線図を描くと図4のようになる。負荷の\( \ \sin \theta ^{\prime } \ \)は，
\[
\begin{eqnarray}
\sin \theta ^{\prime }&=&\sqrt {1-\cos ^{2}\theta ^{\prime }} \\[ 5pt ] &=&\sqrt {1-0.8 ^{2} } \\[ 5pt ] &=&0.714 \ 1 \\[ 5pt ] \end{eqnarray}
\] となり，線路損失は変わらなかったので配電線を流れる電流\( \ I=30.66 \ \mathrm {[A]} \ \)は変わらないから，電圧降下の近似式より，このときの負荷の端子電圧\( \ V_{r}^{\prime} \ \mathrm {[A]} \ \)は，ワンポイント解説「1.三相\( \ 3 \ \)線式送電線の電圧降下の近似式」の通り，
\[
\begin{eqnarray}
V_{s}-V_{r}^{\prime}&=&\sqrt {3}I\left( R\cos \theta ^{\prime }+X\sin \theta ^{\prime } \right) \\[ 5pt ] V_{r}^{\prime}&=&V_{s}-\sqrt {3}I\left( R\cos \theta ^{\prime }+X\sin \theta ^{\prime } \right) \\[ 5pt ] &=&6 \ 600-\sqrt {3}\times 30.66\times \left( 2.25\times 0.8 +1.75\times 0.6 \right) \\[ 5pt ] &≒&6 \ 449 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，負荷に供給される電力\( \ W_{2} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
W_{2}&=&\sqrt {3}V_{r}^{\prime }I\cos \theta ^{\prime } \\[ 5pt ] &=&\sqrt {3}\times 6 \ 449 \times 30.66 \times 0.8 \\[ 5pt ] &≒&274 \ 000 \ \mathrm {[W]}　→　274 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※上記模範解答は精度を上げるため受電端電圧を求めていますが，受電端電圧はほとんど変化しないとして，
\[
\begin{eqnarray}
W_{2}&=&\sqrt {3}V_{r}I\cos \theta ^{\prime } \\[ 5pt ] &=&\sqrt {3}\times 6 \ 450 \times 30.66 \times 0.8 \\[ 5pt ] &≒&274 \ 000 \ \mathrm {[W]}　→　274 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求めても電験の本番では問題ないと考えられます。