《電力》〈水力〉[H21:問1]部分負荷運転している水力発電所の流量に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

水力発電所において，有効落差\( \ 100 \ \mathrm {[m]} \ \)，水車効率\( \ 92 \ \mathrm {[％]} \ \)，発電機効率\( \ 94 \ \mathrm {[％]} \ \)，定格出力\( \ 2 \ 500 \ \mathrm {[kW]} \ \)の水車発電機が\( \ 80 \ \mathrm {[％]} \ \)負荷で運転している。

このときの流量\( \ \mathrm {[m^{3} / s]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 1.76 \ \)　　(2)　\( \ 2.36 \ \)　　(3)　\( \ 3.69 \ \)　　(4)　\( \ 17.3 \ \)　　(5)　\( \ 23.1 \ \)

【ワンポイント解説】

部分負荷時の水力発電所の使用水量に関する問題です。
水力発電所の出力を求める公式は非常によく使用する公式となりますので，必ず理解しておくようにしましょう。

1.水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)
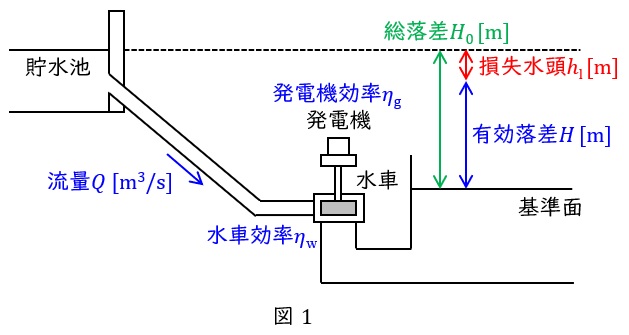
水力発電所の使用水量\( \ Q \ \mathrm {[m^{3}／s]} \ \)，有効落差\( \ H \ \mathrm {[m]} \ \)，水車効率\( \ \eta _{\mathrm {w}} \ \)，発電機効率\( \ \eta _{\mathrm {g}} \ \)とすると，発電機の出力\( \ P \ \mathrm {[kW]} \ \)は，重力加速度\( \ 9.8 \ \mathrm {m / s^{2}} \ \)及び水の密度\( \ 1 \ 000 \ \mathrm {kg / m^{3}} \ \)を考慮すると，
\[
\begin{eqnarray}
P &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(2)
\( \ 80 \ \mathrm {[％]} \ \)負荷での出力\( \ P \ \mathrm {[kW]} \ \)は，定格出力\( \ P_{\mathrm {n}}=2 \ 500 \ \mathrm {[kW]} \ \)であることから，
\[
\begin{eqnarray}
P &=&0.8P_{\mathrm {n}} \\[ 5pt ] &=&0.8\times 2 \ 500 \\[ 5pt ] &=&2 \ 000 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，このときの流量\( \ Q \ \mathrm {[m^{3}／s]} \ \)は，有効落差\( \ H=100 \ \mathrm {[m]} \ \)，水車効率\( \ \eta _{\mathrm {w}}=0.92 \ \)，発電機効率\( \ \eta _{\mathrm {g}}=0.94 \ \)であるから，ワンポイント解説「1.水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)」の通り，
\[
\begin{eqnarray}
P &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \\[ 5pt ] Q &=&\frac {P}{9.8H\eta _{\mathrm {w}}\eta _{\mathrm {g}}} \\[ 5pt ] &=&\frac {2 \ 000}{9.8\times 100\times 0.92\times 0.94} \\[ 5pt ] &≒&2.36 \ \mathrm {[m^{3}／s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。