《電力》〈配電〉[H28:問17]バランサを接続した単相3線式配電線路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

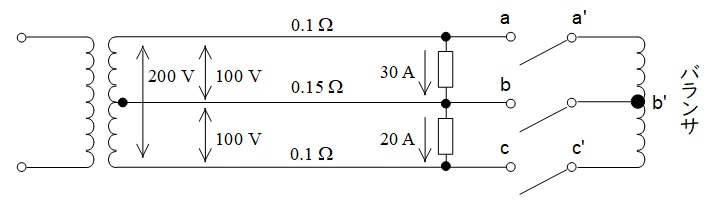
図のような，線路抵抗をもった\( \ \mathrm{100 / 200 \ V} \ \)単相3線式配電線路に，力率が\( \ \mathrm{100 \ ％} \ \)で電流がそれぞれ\( \ \mathrm{30 \ A} \ \)及び\( \ \mathrm{20 \ A} \ \)の二つの負荷が接続されている。この配電線路にバランサを接続した場合について，次の(a)及び(b)の問に答えよ。
ただし，バランサの接続前後で負荷電流は変化しないものとし，線路抵抗以外のインピーダンスは無視するものとする。

(a)　バランサ接続後\( \ a^{\prime }-b^{\prime } \ \)間に流れる電流の値\( \ \mathrm {[ A ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 5 \ \)　　(2)　\( \ 10 \ \)　　(3)　\( \ 20 \ \)　　(4)　\( \ 25 \ \)　　(5)　\( \ 30 \ \)

(b)　バランサ接続前後の線路損失の変化量の値\( \ \mathrm {[ W ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 20 \ \)　　(2)　\( \ 65 \ \)　　(3)　\( \ 80 \ \)　　(4)　\( \ 125 \ \)　　(5)　\( \ 145 \ \)

【ワンポイント解説】

バランサの問題は近年出題されていなかったので，受験生には厳しい問題であったかもしれません。バランサの特性を理解しておきましょう。

1.バランサ
問題図の回路の右側に取りつけた，巻線比\( \ 1:1 \ \)の単相変圧器で，負荷の不平衡や異常電圧を抑制させ，負荷電流を平衡させるものです。以下の特徴があります。
①中性点電流が零となる。
②単相変圧器（バランサ）の上下に流れる電流の大きさが等しい。

【解答】

(a)解答：(1)
バランサ接続前後の回路の状態を図1に示す。

図1より，バランサを流れる電流\( \ I_{\mathrm {B}} \ \)とバランサ接続前の中性点を流れる電流\( \ I_{\mathrm {n}} \ \)の関係は，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&2I_{\mathrm {B}} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
I_{\mathrm {B}} &=& \frac {I_{\mathrm {n}}}{2} \\[ 5pt ] &=& \frac {10}{2} \\[ 5pt ] &=& 5 \ \mathrm {[ A ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
図1(a)より，バランサ接続前の線路損失\( \ W_{1} \ \)は，
\[
\begin{eqnarray}
W_{1} &=& 0.1 {I_{\mathrm {a}}}^{2} +0.15 {I_{\mathrm {n}}}^{2} + 0.1{I_{\mathrm {c}}}^{2} \\[ 5pt ] &=& 0.1 \times {30}^{2} +0.15 \times {10}^{2} + 0.1\times {20}^{2} \\[ 5pt ] &=& 145 \ \mathrm {[ W ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。次に図1(b)において，
\[
\begin{eqnarray}
I_{\mathrm {a}} &=& 30- I_{\mathrm {B}} \\[ 5pt ] &=& 30- 5 \\[ 5pt ] &=& 25 \ \mathrm {[ A ]} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
I_{\mathrm {c}} &=& 20+ I_{\mathrm {B}} \\[ 5pt ] &=& 20+ 5 \\[ 5pt ] &=& 25 \ \mathrm {[ A ]} \\[ 5pt ] \end{eqnarray}
\] であるから，バランサ接続後の線路損失\( \ W_{2} \ \)は，
\[
\begin{eqnarray}
W_{2} &=& 0.1 {I_{\mathrm {a}}}^{2} +0.15 {I_{\mathrm {n}}}^{2} + 0.1{I_{\mathrm {c}}}^{2} \\[ 5pt ] &=& 0.1 \times {25}^{2} +0.15 \times {0}^{2} + 0.1\times {25}^{2} \\[ 5pt ] &=& 125 \ \mathrm {[ W ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，バランサ接続前後の線路損失の変化量\( \ \Delta W \ \)は，
\[
\begin{eqnarray}
\Delta W &=& W_{1}-W_{2} \\[ 5pt ] &=& 145-125 \\[ 5pt ] &=& 20 \ \mathrm {[ W ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。