《電力》〈送電〉[H21:問11]三相３線式地中電線路の誘電体損の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

電圧\( \ 33 \ \mathrm {[kV]} \ \)，周波数\( \ 60 \ \mathrm {[Hz]} \ \)，こう長\( \ 2 \ \mathrm {[km]} \ \)の交流三相\( \ 3 \ \)線式地中電線路がある。ケーブルの心線\( \ 1 \ \)線当たりの静電容量が\( \ 0.24 \ \mathrm {[\mu F / km]} \ \)，誘電正接が\( \ 0.03 \ \mathrm {[％]} \ \)であるとき，このケーブルの心線\( \ 3 \ \)線合計の誘電体損\( \ \mathrm {[W]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 9.4 \ \)　　(2)　\( \ 19.7 \ \)　　(3)　\( \ 29.5 \ \)　　(4)　\( \ 59.1 \ \)　　(5)　\( \ 177 \ \)

【ワンポイント解説】

ケーブルの誘電体損に関する問題です。
公式の丸暗記をしていても解ける問題となりますが，この公式に関しては等価回路とベクトル図から誘電体損の公式を導出できるレベルになった方が良いかなと思います。

1.誘電体損
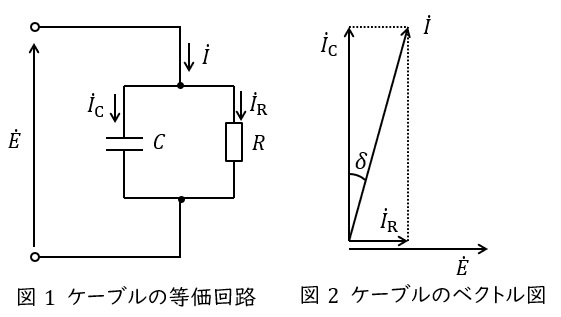
ケーブルは誘電体を金属で挟んだコンデンサのような構造をしているため，損失分も合わせ一相分等価回路は図1のように抵抗\( \ R \ \mathrm {[\Omega ]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)の並列回路となり，図2のベクトル図に示すような電流が流れます。ただし，\( \ \dot E \ \mathrm {[V]} \ \)はケーブルに加わる電圧の相電圧となります。
この時のコンデンサ分に流れる電流\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)に対する抵抗分に流れる電流\( \ I_{\mathrm {R}} \ \mathrm {[A]} \ \)の割合\( \ \displaystyle \frac {I_{\mathrm {R}}}{I_{\mathrm {C}}}=\tan \delta \ \)を誘電正接と呼び，ケーブルが劣化してくると大きくなります。
ケーブルの誘電体損\( \ W_{\mathrm {d}} \ \mathrm {[W]} \ \)は，ケーブルに加わる電圧（線間電圧）を\( \ V \ \mathrm {[V]} \ \)，周波数を\( \ f \ \mathrm {[Hz]} \ \)，角周波数を\( \ \omega =2\pi f \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
W_{\mathrm {d}}&=&3\frac {V}{\sqrt {3}}I_{\mathrm {R}} \\[ 5pt ] &=&3\frac {V}{\sqrt {3}}I_{\mathrm {C}}\tan \delta \\[ 5pt ] &=&3\frac {V}{\sqrt {3}}\left( \omega C\frac {V}{\sqrt {3}}\right) \tan \delta \\[ 5pt ] &=&\omega CV^{2}\tan \delta \\[ 5pt ] &=&2\pi f CV^{2}\tan \delta \\[ 5pt ] \end{eqnarray}
\] となり，誘電体損は電圧\( \ V \ \mathrm {[V]} \ \)の\( \ 2 \ \)乗に比例し，周波数\( \ f \ \mathrm {[Hz]} \ \)，誘電正接\( \ \tan \delta \ \)に比例することがわかります。

【解答】

解答：(4)
ケーブルの心線\( \ 1 \ \)線当たりの静電容量\( \ C \ \mathrm {[F]} \ \)は，こう長が\( \ 2 \ \mathrm {km} \ \)であるから，
\[
\begin{eqnarray}
C&=&0.24\times 10^{-6}\times 2 \\[ 5pt ] &=&4.8\times 10^{-5} \ \mathrm {[F]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，ケーブルの誘電体損\( \ W_{\mathrm {d}} \ \mathrm {[W]} \ \)は，ワンポイント解説「1.誘電体損」の通り，
\[
\begin{eqnarray}
W_{\mathrm {d}}&=&2\pi f CV^{2}\tan \delta \\[ 5pt ] &=&2\pi \times 60\times 4.8\times 10^{-5}\times \left( 33\times 10^{3}\right) ^{2}\times \frac {0.03}{100} \\[ 5pt ] &≒&59.1 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。