Contents
【問題】
【難易度】★★★☆☆(普通)
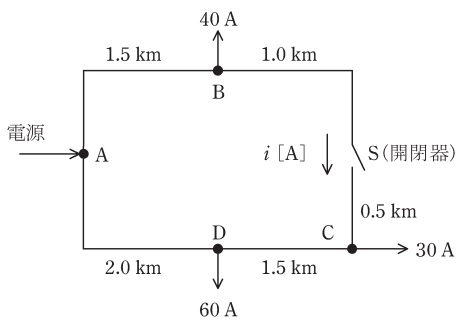
図のような系統構成の三相\( \ 3 \ \)線式配電線路があり,開閉器\( \ \mathrm {S} \ \)は開いた状態にある。各配電線の\( \ \mathrm {B} \ \)点,\( \ \mathrm {C} \ \)点,\( \ \mathrm {D} \ \)点には図のとおり負荷が接続されており,各点の負荷電流は\( \ \mathrm {B} \ \)点\( \ 40 \ \mathrm {A} \ \),\( \ \mathrm {C} \ \)点\( \ 30 \ \mathrm {A} \ \),\( \ \mathrm {D} \ \)点\( \ 60 \ \mathrm {A} \ \)一定とし,各負荷の力率は\( \ 100 \ \mathrm {%} \ \)とする。
各区間のこう長は\( \ \mathrm {A}-\mathrm {B} \ \)間\( \ 1.5 \ \mathrm {km} \ \),\( \ \mathrm {B}-\mathrm {S} \ \)(開閉器)間\( \ 1.0 \ \mathrm {km} \ \),\( \ \mathrm {S} \ \)(開閉器)\( \ -\mathrm {C} \ \)間\( \ 0.5 \ \mathrm {km} \ \),\( \ \mathrm {C}-\mathrm {D} \ \)間\( \ 1.5 \ \mathrm {km} \ \),\( \ \mathrm {D}-\mathrm {A} \ \)間\( \ 2.0 \ \mathrm {km} \ \)である。
ただし,電線\( \ 1 \ \)線当たりの抵抗は\( \ 0.2 \ \mathrm {\Omega /km} \ \)とし,リアクタンスは無視するものとして,次の(a)及び(b)の問に答えよ。
(a) 電源\( \ \mathrm {A} \ \)点から見た\( \ \mathrm {C} \ \)点の電圧降下の値\( \ \mathrm {[V]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,電圧は相間電圧とする。
(1) \( \ 41.6 \ \) (2) \( \ 45.0 \ \) (3) \( \ 57.2 \ \) (4) \( \ 77.9 \ \) (5) \( \ 90.0 \ \)
(b) 開閉器\( \ \mathrm {S} \ \)を投入した場合,開閉器\( \ \mathrm {S} \ \)を流れる電流\( \ i \ \)の値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 20.0 \ \) (2) \( \ 25.4 \ \) (3) \( \ 27.5 \ \) (4) \( \ 43.8 \ \) (5) \( \ 65.4 \ \)
【ワンポイント解説】
ループ配電に関する問題です。ループ配電の問題は,ある一点の区間の電流を置き,全区間をループしたときの電圧降下の合計が零となるように求めると良いです。(マイナスの電流が流れる場合は電圧上昇となります。)
本問のレベルは(a)は基本問題,(b)が標準問題です。合格するためには,(b)のループ配電に関する問題を解けるようになることも重要ではありますが,(a)の問題を取りこぼさないようにすることがさらに重要となります。
1.配電線の電圧降下の近似式
①単相\( \ 2 \ \)線式配電線の電圧降下
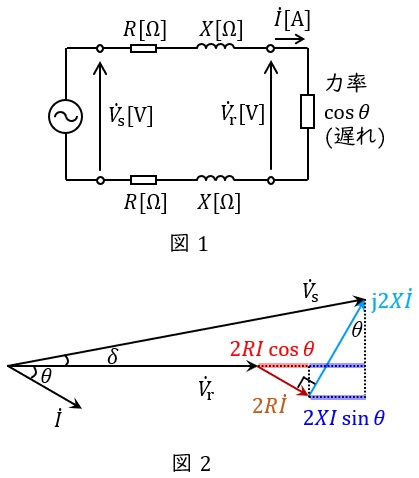
単相\( \ 2 \ \)線式線路は図1のような回路になり,負荷に対して供給される線路と戻りの線路の\( \ 2 \ \)段階で電圧降下が発生します。したがって,負荷の力率が遅れ力率\( \ \cos \theta \ \)であるときのベクトル図を描くと図2のようになります。
図2のベクトル図において,\( \ {\dot V}_{\mathrm {s}} \ \)と\( \ {\dot V}_{\mathrm {r}} \ \)の位相差が十分に小さいと仮定すると,線路の電圧降下\( \ \varepsilon =V_{\mathrm {s}}-V_{\mathrm {r}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {s}}&≃&V_{\mathrm {r}}+2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
V_{\mathrm {s}}-V_{\mathrm {r}}&=&2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
\varepsilon &=&2I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
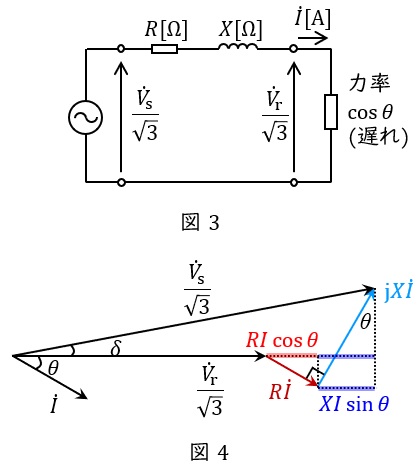
②三相\( \ 3 \ \)線式配電線の電圧降下
三相回路においては,一相分の等価回路及びベクトル図は図3及び図4のように描くことができ,三相分の電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\frac {V_{\mathrm {s}}}{\sqrt {3}}&≃&\frac {V_{\mathrm {r}}}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ]
\frac {V_{\mathrm {s}}}{\sqrt {3}}-\frac {V_{\mathrm {r}}}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ]
V_{\mathrm {s}}-V_{\mathrm {r}}&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ]
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【解答】
(a)解答:(4)
開閉器\( \ \mathrm {S} \ \)が開いた状態にあるとき,電流は点\( \ \mathrm {A}-\mathrm {D}-\mathrm {C} \ \)と流れ,\( \ \mathrm {A}-\mathrm {D} \ \)間を流れる電流\( \ I_{\mathrm {AD}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {AD}} &=&60+30 \\[ 5pt ]
&=&90 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ \mathrm {D}-\mathrm {C} \ \)を流れる電流\( \ I_{\mathrm {DC}} \ \)は\( \ 30 \ \mathrm {[A]} \ \)である。
また,\( \ \mathrm {A}-\mathrm {D} \ \)間の抵抗\( \ R_{\mathrm {AD}} \ \)及び\( \ \mathrm {D}-\mathrm {C} \ \)間の抵抗\( \ R_{\mathrm {DC}} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {AD}} &=&2.0\times 0.2 \\[ 5pt ]
&=&0.4 \ \mathrm {[\Omega ]} \\[ 5pt ]
R_{\mathrm {DC}} &=&1.5\times 0.2 \\[ 5pt ]
&=&0.3 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,電源\( \ \mathrm {A} \ \)点から見た\( \ \mathrm {C} \ \)点の電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は,ワンポイント解説「1.配電線の電圧降下の近似式」より,
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I_{\mathrm {AD}}\cdot R_{\mathrm {AD}} +\sqrt {3}I_{\mathrm {DC}}\cdot R_{\mathrm {DC}} \\[ 5pt ]
&=&\sqrt {3}\times 90\times 0.4 +\sqrt {3}\times 30 \times 0.3 \\[ 5pt ]
&≒&77.9 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(2)
各点の負荷電流は\( \ \mathrm {B} \ \)点\( \ 40 \ \mathrm {A} \ \),\( \ \mathrm {C} \ \)点\( \ 30 \ \mathrm {A} \ \),\( \ \mathrm {D} \ \)点\( \ 60 \ \mathrm {A} \ \)なので,電源から\( \ \mathrm {A} \ \)点に供給される電流はすべてを合わせた\( \ 130 \ \mathrm {A} \ \)である。
また,\( \ \mathrm {A}-\mathrm {B} \ \)間の抵抗\( \ R_{\mathrm {AB}} \ \)及び\( \ \mathrm {B}-\mathrm {C} \ \)間の抵抗\( \ R_{\mathrm {BC}} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {AB}} &=&1.5\times 0.2 \\[ 5pt ]
&=&0.3 \ \mathrm {[\Omega ]} \\[ 5pt ]
R_{\mathrm {BC}} &=&\left( 1.0+0.5\right) \times 0.2 \\[ 5pt ]
&=&0.3 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
である。
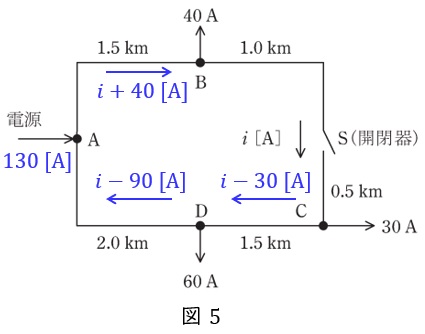
開閉器\( \ \mathrm {S} \ \)を流れる電流\( \ i \ \)を基準とすると,各部の電流は図5のようになり,ループ内の電圧降下が零であることから,
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I_{\mathrm {BC}}\cdot R_{\mathrm {BC}} +\sqrt {3}I_{\mathrm {CD}}\cdot R_{\mathrm {CD}}+\sqrt {3}I_{\mathrm {DA}}\cdot R_{\mathrm {DA}}+\sqrt {3}I_{\mathrm {AB}}\cdot R_{\mathrm {AB}} \\[ 5pt ]
0&=&\sqrt {3}i\times 0.3+\sqrt {3}\left( i-30\right) \times 0.3+\sqrt {3}\left( i-90\right) \times 0.4+\sqrt {3}\left( i+40\right) \times 0.3 \\[ 5pt ]
0&=&1.3\times \sqrt {3}i-33\sqrt {3} \\[ 5pt ]
1.3\times \sqrt {3}i&=&33\sqrt {3} \\[ 5pt ]
i&≒&25.4 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは