《電力》〈送電〉[H21:問7]交流三相3線式送電線路の送電電力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

交流三相\( \ 3 \ \)線式\( \ 1 \ \)回線の送電線路があり，受電端に遅れ力率角\( \ \theta \ \mathrm {[rad]} \ \)の負荷が接続されている。送電端の線間電圧を\( \ V_{s} \ \mathrm {[V]} \ \)，受電端の線間電圧を\( \ V_{r} \ \mathrm {[V]} \ \)，その間の相差角は\( \ \delta \ \mathrm {[rad]} \ \)である。

受電端の負荷に供給されている三相有効電力\( \ \mathrm {[W]} \ \)を表す式として，正しいのは次のうちどれか。

ただし，送電端と受電端の間における電線\( \ 1 \ \)線当たりの誘導性リアクタンスは\( \ X \ \mathrm {[\Omega ]} \ \)とし，線路の抵抗，静電容量は無視するものとする。

　(1)　\( \ \displaystyle \frac {V_{s}V_{r}}{X}\cos \delta \ \)　　(2)　\( \ \displaystyle \frac {\sqrt {3}V_{s}V_{r}}{X}\cos \theta \ \)　　(3)　\( \ \displaystyle \frac {V_{s}V_{r}}{X}\sin \delta \ \)

　(4)　\( \ \displaystyle \frac {\sqrt {3}V_{s}V_{r}}{X}\sin \delta \ \)　　(5)　\( \ \displaystyle \frac {V_{s}V_{r}}{X\sin \delta }\cos \theta \ \)　　

【ワンポイント解説】

送電線の三相有効電力に関する問題です。
もちろんワンポイント解説のように有効電力を導出できるようになるのが理想ですが，本問の解答は公式として覚えておくと良いでしょう。

1.送電線の送電電力
送電端の電圧が\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)，受電端の電圧が\( \ V_{\mathrm {r}} \ \mathrm {[V]} \ \)，送電線の\( \ 1 \ \)線あたりのリアクタンスが\( \ x \ \mathrm {[\Omega ]} \ \)（抵抗分は無視できるものとします），送電線に流れる電流が\( \ I \ \mathrm {[A]} \ \)であるとすると，送電線の単線結線図は図1，ベクトル図は図2のように描くことができます。ただし，\( \ \delta \ \mathrm {[rad]} \ \)は送電端電圧と受電端電圧の相差角，\( \ \theta \ \mathrm {[rad]} \ \)は負荷の力率角，\( \ E_{\mathrm {s}} \ \mathrm {[V]} \ \)は送電端の相電圧，\( \ E_{\mathrm {r}} \ \mathrm {[V]} \ \)は受電端の相電圧です。

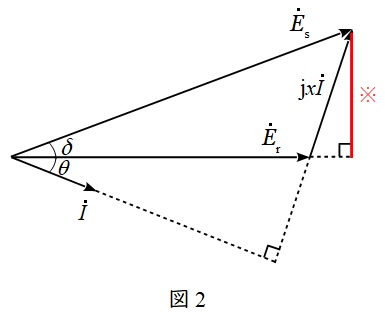
このとき，負荷電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P&=&\sqrt {3} V_{\mathrm {r}}I\cos \theta \\[ 5pt ] \end{eqnarray}
\] で求めることができ，図2の※線を求める式より，
\[
\begin{eqnarray}
xI\cos \theta &=&E_{\mathrm {s}}\sin \delta \\[ 5pt ] I\cos \theta &=&\frac {E_{\mathrm {s}}}{x}\sin \delta \\[ 5pt ] &=&\frac {V_{\mathrm {s}}}{\sqrt {3}x}\sin \delta \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
P&=&\sqrt {3} V_{\mathrm {r}}I\cos \theta \\[ 5pt ] &=&\sqrt {3} V_{\mathrm {r}}\cdot \frac {V_{\mathrm {s}}}{\sqrt {3}x}\sin \delta \\[ 5pt ] &=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{x}\sin \delta \\[ 5pt ] \end{eqnarray}
\] となります。上式は\( \ P=\sqrt {3} V_{\mathrm {r}}I\cos \theta \ \)と合わせて公式として覚えておきましょう。

【解答】

解答：(3)
三相有効電力\( \ P \ \mathrm {[W]} \ \)は，ワンポイント解説「1.送電線の送電電力」の通り，
\[
\begin{eqnarray}
P&=&\frac {V_{s}V_{r}}{X}\sin \delta \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。