《電力》〈変電〉[H28:問16]事故時に流れる電流に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図に示すように，発電機，変圧器と公称電圧\( \ \mathrm{66 \ kV} \ \)で運転される送電線からなる系統があるとき，次の(a)及び(b)の問に答えよ。ただし，中性点接地抵抗は図の変圧器のみに設置され，その値は\( \ \mathrm{300 \ \Omega } \ \)とする。

(a)　\( \ \mathrm{A} \ \)点で\( \ \mathrm{100 \ \Omega } \ \)の抵抗を介して一線地絡事故が発生した。このときの地絡電流の値\( \ \mathrm {[ A ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，発電機，発電機と変圧器間，変圧器及び送電線のインピーダンスは無視するものとする。

　(1)　\( \ 95 \ \)　　(2)　\( \ 127 \ \)　　(3)　\( \ 165 \ \)　　(4)　\( \ 381 \ \)　　(5)　\( \ 508 \ \)

(b)　\( \ \mathrm{A} \ \)点で三相短絡事故が発生した。このときの三相短絡電流の値\( \ \mathrm {[ A ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，発電機の容量は\( \ \mathrm{10000 \ kV\cdot A } \ \)，出力電圧\( \ \mathrm{6.6 \ kV} \ \)，三相短絡時のリアクタンスは自己容量ベースで\( \ \mathrm {25 \ ％} \ \)，変圧器容量は\( \ \mathrm{10000 \ kV\cdot A } \ \)，変圧比は\( \ \mathrm{6.6 \ kV \ / \ 66 \ kV \ }\)，リアクタンスは自己容量ベースで\( \ \mathrm {10 \ ％} \ \)，\( \ \mathrm{66 \ kV} \ \)送電線のリアクタンスは，\( \ \mathrm{10000 \ kV\cdot A } \ \)ベースで\( \ \mathrm {5 \ ％} \ \)とする。なお，発電機と変圧器間のインピーダンスは無視する。また，発電機，変圧器及び送電線の抵抗は無視するものとする。

　(1)　\( \ 33 \ \)　　(2)　\( \ 219 \ \)　　(3)　\( \ 379 \ \)　　(4)　\( \ 656 \ \)　　(5)　\( \ 3019 \ \)

【ワンポイント解説】

事故時の計算にパーセントインピーダンスが用いられます。毎年のようにパーセントインピーダンスの問題は出題されるので、よく理解しておくようにしましょう。

1.三相回路における基準電流の導出
基準電圧を\( \ V_{\mathrm{n}} \ \)，基準容量を\( \ P_{\mathrm{n}} \ \)とすると，基準電流\( \ I_{\mathrm{n}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm{n}}&=&\frac {P_{\mathrm{n}}}{\sqrt {3}V_{\mathrm{n}}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.三相短絡電流の計算式
線路のパーセントインピーダンスを\( \ ％Z \ \)，基準電流\( \ I_{\mathrm{n}} \ \)とすると，三相短絡電流\( \ I_{\mathrm{s}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm{s}}&=&\frac {100}{％Z}I_{\mathrm{n}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

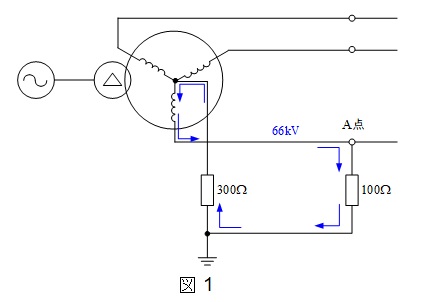
(a)解答：(1)
一線地絡事故が発生した時の回路は図1のようになる。故障相の相電圧は\( \ \displaystyle \frac {66}{\sqrt{3}} \ \mathrm {[ kV ]} \ \)であるから，一線地絡電流\( \ I_{\mathrm{g}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm{g}} &=& \frac {\frac {66000}{\sqrt{3}}}{100+300} \\[ 5pt ] &≒& 95.3　→ 95 \ \mathrm {[ A ]}
\end{eqnarray}
\] と求められる。

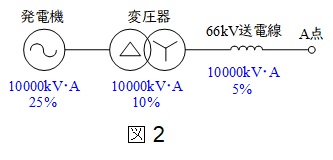
(b)解答：(2)
題意を整理すると図2のようになる。図2より，\( \ \mathrm{A} \ \)点から見たパーセントインピーダンス\( \ \mathrm{％}Z \ \)は
\[
\begin{eqnarray}
\mathrm{％}Z &=& 25 +10 + 5 \\[ 5pt ] &=& 40 \ \mathrm {[ ％ ]}
\end{eqnarray}
\] である。また，\( \ \mathrm{66 \ kV} \ \)送電線の定格電流\( \ I_{\mathrm{n}} \ \)は，ワンポイント解説「1.三相回路における基準電流の導出」の通り，
\[
\begin{eqnarray}
I_{\mathrm{n}} &=& \frac {P_{\mathrm{n}}}{\sqrt {3}V_{\mathrm{n}}} \\[ 5pt ] &=& \frac {10000}{\sqrt {3}\times 66} \\[ 5pt ] &≒& 87.48 \ \mathrm {[ A ]}
\end{eqnarray}
\] であるから，三相短絡電流\( \ I_{\mathrm{s}} \ \)は，ワンポイント解説「2.三相短絡電流の計算式」の通り，
\[
\begin{eqnarray}
I_{\mathrm{s}}&=&\frac {100}{％Z}I_{\mathrm{n}} \\[ 5pt ] &=& \frac {100}{40}\times 87.48 \\[ 5pt ] &≒& 219 \ \mathrm {[ A ]}
\end{eqnarray}
\] と求められる。