《電力》〈変電〉[H22:問6]三相コンデンサを設置することによる配電線の力率改善に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

\( \ 50 \ \mathrm {[Hz]} \ \)，\( \ 200 \ \mathrm {[V]} \ \)の三相配電線の受電端に，力率\( \ 0.7 \ \)，\( \ 50 \ \mathrm {[kW]} \ \)の誘導性三相負荷が接続されている。 この負荷と並列に三相コンデンサを挿入して，受電端での力率を遅れ\( \ 0.8 \ \)に改善したい。

挿入すべき三相コンデンサの無効電力容量\( \ \mathrm {[kV\cdot A]} \ \)の値として, 最も近いのは次のうちどれか。

　(1)　\( \ 4.58 \ \)　　(2)　\( \ 7.80 \ \)　　(3)　\( \ 13.5 \ \)　　(4)　\( \ 19.0 \ \)　　(5)　\( \ 22.5 \ \)　　

【ワンポイント解説】

力率改善に関する問題です。
根号の計算を伴うので少し計算量はありますが，かなりパターン化されている問題で類題の出題頻度も高い問題です。
有効電力と無効電力の関係や電卓の扱いに慣れ，\( \ 5 \ \)分程度を目標に解けるようになりましょう。

1.有効電力\( \ P \ \)と無効電力\( \ Q \ \)
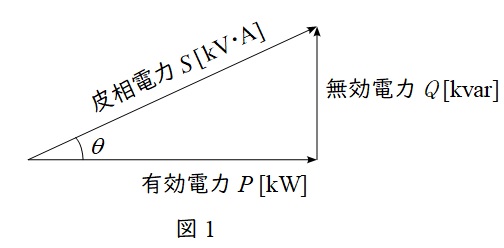
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図1のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図1において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
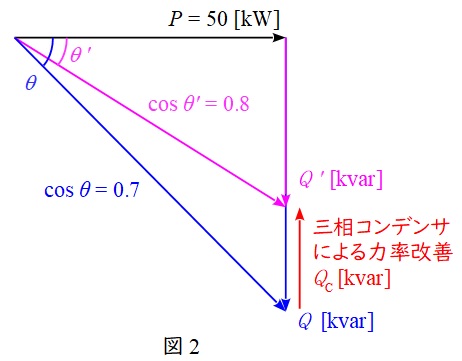
力率改善前後のベクトル図を描くと図2のようになる。
力率改善前の無効電力\( \ Q \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q &=&\frac {P}{\cos \theta }\times \sin \theta \\[ 5pt ] &=&\frac {P}{\cos \theta }\times \sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\frac {50}{0.7}\times \sqrt {1-0.7 ^{2}} \\[ 5pt ] &≒&51.01 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] であり，力率改善後の無効電力\( \ Q^{\prime } \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q^{\prime } &=&\frac {P}{\cos \theta ^{\prime }}\times \sin \theta ^{\prime } \\[ 5pt ] &=&\frac {P}{\cos \theta ^{\prime }}\times \sqrt {1-\cos ^{2}\theta ^{\prime }} \\[ 5pt ] &=&\frac {50}{0.8}\times \sqrt {1-0.8 ^{2}} \\[ 5pt ] &=&37.5 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，三相コンデンサの無効電力容量\( \ Q_{\mathrm {C}} \ \mathrm {[kvar]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {C}} &=&Q-Q^{\prime } \\[ 5pt ] &=&51.01-37.5 \\[ 5pt ] &≒&13.5 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。