Contents
【問題】
【難易度】★★★☆☆(普通)
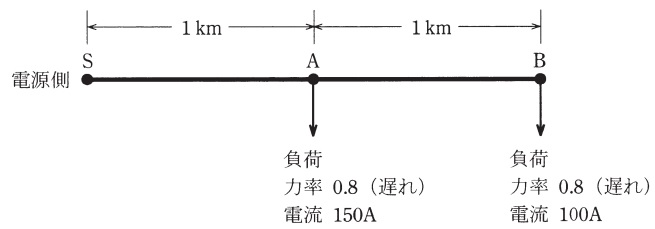
図のような三相\( \ 3 \ \)線式配電線路において,電源側\( \ \mathrm {S} \ \)点の線間電圧が\( \ 6900 \ \mathrm {[V]} \ \)のとき,\( \ \mathrm {B} \ \)点の線間電圧\( \ \mathrm {[V]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,配電線\( \ 1 \ \)線当たりの抵抗は\( \ 0.3 \ \mathrm {[\Omega / km]} \ \),リアクタンスは\( \ 0.2 \ \mathrm {[\Omega / km]} \ \)とする。また,計算においては\( \ \mathrm {S} \ \)点,\( \ \mathrm {A} \ \)点及び\( \ \mathrm {B} \ \)点における電圧の位相差が十分小さいとの仮定に基づき適切な近似を用いる。
(1) \( \ 6522 \ \) (2) \( \ 6646 \ \) (3) \( \ 6682 \ \) (4) \( \ 6774 \ \) (5) \( \ 6795 \ \)
【ワンポイント解説】
送電線の電圧降下の式は丸暗記するのではなく,できるだけベクトル図を思い出しながら理解するようにしましょう。三相\( \ 3 \ \)線式の場合は\( \ \sqrt {3} \ \)が必要であり,忘れやすいので注意するようにしましょう。たいてい\( \ \sqrt {3} \ \)を忘れた場合の誤答が用意されています。(本問の場合(4)が該当)
1.配電線の電圧降下の近似式
①単相回路の電圧降下
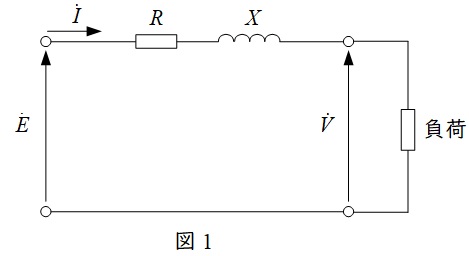
図1のような回路において,ベクトル図を描くと図2のようになります。
図2のベクトル図において,\(\dot E \)と\(\dot V\)の位相差が十分に小さいと仮定すると,線路の電圧降下\(\varepsilon =E-V\)は,
\[
\begin{eqnarray}
E&≃&V+RI\cos \theta +XI\sin \theta \\[ 5pt ]
E-V&=&RI\cos \theta +XI\sin \theta \\[ 5pt ]
\varepsilon &=&I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。

②三相3線式送電線の電圧降下
三相回路においても,一相分の等価回路及びベクトル図は図1及び図2のように描くことができ,三相分の電圧降下\(\varepsilon \)は,
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
※従って本問においては\(\sqrt {3}\)の計算忘れに注意が必要です。
【解答】
解答:(3)
送電線の\( \ \mathrm {S} \ \)-\( \ \mathrm {A} \ \)点間,\( \ \mathrm {A} \ \)-\( \ \mathrm {B} \ \)点間を流れる電流\( \ I_{\mathrm {SA}} \ \),\( \ I_{\mathrm {AB}} \ \)の大きさは,
\[
\begin{eqnarray}
I_{\mathrm {SA}}&=&150+100 \\[ 5pt ]
&=&250 \ \mathrm {[A]} \\[ 5pt ]
I_{\mathrm {AB}}&=&100 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であり,
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&\sqrt {1-0.8^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
であるから,それぞれの電圧降下\( \ v_{\mathrm {SA}} \ \),\( \ v_{\mathrm {AB}} \ \)は,ワンポイント解説「1.配電線の電圧降下の近似式」より,
\[
\begin{eqnarray}
v_{\mathrm {SA}} &=&\sqrt {3}I_{\mathrm {SA}}\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
&=&\sqrt {3}\times 250 \times \left( 0.3 \times 0.8 +0.2\times 0.6 \right) \\[ 5pt ]
&≒&155.9 \ \mathrm {[V]} \\[ 5pt ]
v_{\mathrm {AB}} &=&\sqrt {3}I_{\mathrm {AB}}\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
&=&\sqrt {3}\times 100 \times \left( 0.3 \times 0.8 +0.2\times 0.6 \right) \\[ 5pt ]
&≒&62.35 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ \mathrm {B} \ \)点の線間電圧\( \ V_{\mathrm {B}} \ \)は,\( \ \mathrm {S} \ \)点の線間電圧が\( \ V_{\mathrm {S}}=6900 \ \mathrm {[V]} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {B}} &=&V_{\mathrm {S}}-v_{\mathrm {SA}}-v_{\mathrm {AB}} \\[ 5pt ]
&=&6900-155.9-62.35 \\[ 5pt ]
&≒&6682 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは