《電力》〈変電〉[H26:問6]配電用変電所の変圧器容量に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

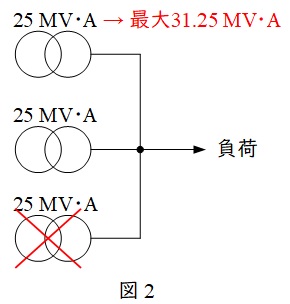
1バンクの定格容量$25 \ \mathrm {MV\cdot A}$の三相変圧器を3バンク有する配電用変電所がある。変圧器1バンクが故障した時に長時間の停電なしに故障発生前と同じ電力を供給したい。

この検討に当たっては，変圧器故障時には，他の変電所に故障発生前の負荷の$10 \ ％$を直ちに切り換えることができるとともに，残りの健全な変圧器は，定格容量の$125 \ ％$まで過負荷することができるものとする。

力率は常に$95 \ ％$(遅れ)で変化しないものとしたとき，故障発生前の変電所の最大総負荷の値$\mathrm {[MW]}$として，最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)　32.9　　(2)　53.4　　(3)　65.9　　(4)　80.1　　(5)　98.9

【ワンポイント解説】

問題の内容が若干理解しにくい内容となっています。変圧器の値が皮相電力$\mathrm {[MV\cdot A]}$であることに注意して解くようにして下さい。

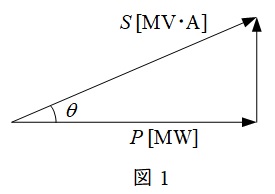
1.皮相電力$S$と有効電力$P$の関係
図1のベクトル図に示すように皮相電力$S$と有効電力$P$の関係は力率角を$\theta$とすると，
$$P=S\cos \theta$$ となります。

【解答】

解答：(3)
題意より，健全な変圧器が過負荷運転できる最大容量は，
$$\begin{eqnarray} 25 \times 1.25 &=&31.25 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}$$ であるから，2台で供給できる最大容量は
$$\begin{eqnarray} 31.25 \times 2 &=&62.5 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}$$ となる。よって，力率が$95 \ ％$(遅れ)であるとき，供給できる電力は，
$$\begin{eqnarray} 62.5 \times 0.95 &=&59.375 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}$$ となる。最大負荷を$P$とすると，故障発生時に他の変電所が負荷の$10 \ ％$を負担できるので，この変電所で負担する負荷は$0.9P$となる。よって，この関係より最大負荷は，
$$\begin{eqnarray} 0.9P &=&59.375 \\[ 5pt ] P &≒&65.972 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}$$ と求められる。