《電力》〈火力〉[R01:問15]汽力発電所のタービン出力及び海水温度に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

復水器の冷却に海水を使用し，運転している汽力発電所がある。このときの復水器冷却水流量は\( \ 30 \ \mathrm {m^{3}／s} \ \)，復水器冷却水が持ち去る毎時熱量は\( \ 3.1\times 10^{9} \ \mathrm {kJ／h} \ \)，海水の比熱容量は\( \ 4.0 \ \mathrm {kJ／\left( kg\cdot K\right) } \ \)，海水の密度は\( \ 1.1\times 10^{3} \ \mathrm {kg／m^{3}} \ \)，タービンの熱消費率は\( \ 8000 \ \mathrm {kJ／\left( kW\cdot h\right) } \ \)である。

この運転状態について，次の(a)及び(b)の問に答えよ。

ただし，復水器冷却水が持ち去る熱以外の損失は無視するものとする。

(a)　タービン出力の値\( \ \mathrm {[MW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(350\)　　(2)　\(500\)　　(3)　\(700\)　　(4)　\(800\)　　(5)　\(1000\)

(b)　復水器冷却水の温度上昇の値\( \ \mathrm {[K]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(3.3\)　　(2)　\(4.7\)　　(3)　\(5.3\)　　(4)　\(6.5\)　　(5)　\(7.9\)

【ワンポイント解説】

本問は様々な公式を利用しますが，なぜその公式になるのかを理解した上で解くことが大事となります。また，汽力発電のメカニズムをよく理解しておくことも重要で，熱損失で最も大きいのは復水器の熱交換で，ボイラ入熱の約半分になり，それにより海水温度は約\( \ 7 \ \)℃上昇し，一般的な発電所ではこの値で設計されていることも理解しましょう。したがって，本問(b)はその知識があれば解けてしまう問題となります。

1.熱量と電力量の関係
\( \ 1 \ \mathrm {[kW\cdot h]} \ \)は\( \ 1 \ \mathrm {[kW]} \ \)の電力で\( \ 1 \ \)時間運転した時の電力量です。
また，\( \ 1 \ \mathrm {[W\cdot s]}=1 \ \mathrm {[J]} \ \)の関係があります。したがって，
\[
\begin{eqnarray}
1 \ \mathrm {[kW\cdot h]}&=&3600 \ \mathrm {[kW\cdot s]} \\[ 5pt ] &=&3600 \ \mathrm {[kJ]} \\[ 5pt ] \end{eqnarray}
\] の関係があります。また，上式から電力と\( \ 1 \ \)時間当たりの熱量の関係は，
\[
\begin{eqnarray}
1 \ \mathrm {[kW]}&=&3600 \ \mathrm {[kJ／h]} \\[ 5pt ] \end{eqnarray}
\] となります。

2.熱消費率\( \ q \ \)
電力量\( \ 1 \ \mathrm {[kW\cdot h]} \ \)を発電するのに必要な熱量\( \ \mathrm {[kJ]} \ \)を示す指標で，火力発電所での効率管理に使用されます。実質的には電力\( \ 1 \ \mathrm {[kW]} \ \)に対する\( \ 1 \ \)時間あたりの熱量\( \ \mathrm {[kJ／h]} \ \)が使用されます。
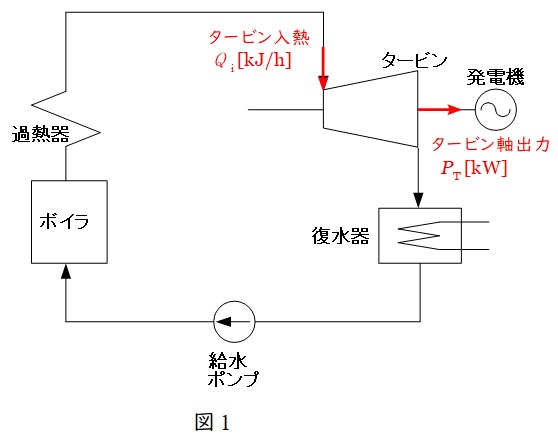
図1においてタービン熱消費率を\( \ q_{\mathrm {t}} \ \)とすると，
\[
\begin{eqnarray}
q_{\mathrm {t}} &=&\frac {Q_{\mathrm {i}}}{P_{\mathrm {T}}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.海水の温度上昇\( \ \Delta T \ \)と熱量\( \ Q \ \)の関係
海水の流量を\( \ W \ \mathrm {[m^{3}／s]} \ \)，海水の比熱容量を\( \ C \ \mathrm {[kJ／\left( kg\cdot K\right) ]} \ \)，海水の密度を\( \ \rho \ \mathrm {[kg／m^{3}]} \ \)，温度上昇を\( \ \Delta T \ \mathrm {[℃]} \ \)とすると，\( \ 1 \ \mathrm {[s]} \ \)当たりに持ち去る熱量\( \ Q \ \mathrm {[kJ／s]} \ \)は，
\[
\begin{eqnarray}
Q &=&C\rho W\Delta T \\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

(a)解答：(3)
ワンポイント解説「1.熱量と電力量の関係」の通り，電力と\( \ 1 \ \)時間当たりの熱量の関係は，
\[
\begin{eqnarray}
1 \ \mathrm {[kW]}&=&3600 \ \mathrm {[kJ／h]} \\[ 5pt ] \end{eqnarray}
\] であるから，\( \ 1 \ \mathrm {[kW]} \ \)で発電するために復水器に流れる熱量\( \ Q_{\mathrm {o}} \ \mathrm {[kJ／h]} \)は，
\[
\begin{eqnarray}
Q_{\mathrm {o}}&=&8000-3600 \\[ 5pt ] &=&4400 \ \mathrm {[kJ／h]} \\[ 5pt ] \end{eqnarray}
\] となる。題意より，復水器冷却水が持ち去る毎時熱量は\( \ 3.1\times 10^{9} \ \mathrm {kJ／h} \ \)であるから，タービン出力\( \ P_{\mathrm {T}} \ \mathrm {[kW]} \)は，
\[
\begin{eqnarray}
P_{\mathrm {T}}&=&\frac {3.1\times 10^{9}}{4400} \\[ 5pt ] &≒&704545 \ \mathrm {[kW]}　→　700 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
ワンポイント解説「3.海水の温度上昇\( \ \Delta T \ \)と熱量\( \ Q \ \)の関係」の通り，\( \ 1 \ \mathrm {[s]} \ \)当たりに持ち去る熱量\( \ Q \ \mathrm {[kJ／s]} \ \)は，温度上昇を\( \ \Delta T \ \mathrm {[℃]} \ \)とすると，
\[
\begin{eqnarray}
Q &=&4.0\times 1.1\times 10^{3}\times 30\Delta T \\[ 5pt ] &=&1.32\times 10^{5}\Delta T \\[ 5pt ] \end{eqnarray}
\] であるので，\( \ 1 \ \mathrm {[h]} \ \)当たりに持ち去る熱量\( \ Q \ \mathrm {[kJ／h]} \ \)は，
\[
\begin{eqnarray}
Q &=&1.32\times 10^{5}\Delta T \times 3600 \\[ 5pt ] &=&4.752\times 10^{8}\Delta T \\[ 5pt ] \end{eqnarray}
\] となる。復水器冷却水が持ち去る毎時熱量は\( \ 3.1\times 10^{9} \ \mathrm {kJ／h} \ \)であるので，
\[
\begin{eqnarray}
3.1\times 10^{9} &=&4.752\times 10^{8}\Delta T \\[ 5pt ] \Delta T&≒&6.52　→　6.5 \ \mathrm {[℃]} \\[ 5pt ] \end{eqnarray}
\] と求められる。