《電力》〈送電〉[R2:問10]架空送電線路の線路定数とその考え方に関する空欄穴埋問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，架空送電線路に関する記述である。

架空送電線路の線路定数には，抵抗，作用インダクタンス，作用静電容量，\( \ \fbox {　 （ア） 　} \ \)コンダクタンスがある。線路定数のうち，抵抗値は，表皮効果により\( \ \fbox {　 （イ） 　} \ \)のほうが増加する。また，作用インダクタンスと作用静電容量は，線間距離\( \ D \ \)と電線半径\( \ r \ \)の比\( \ D／r \ \)に影響される。\( \ D／r \ \)の値が大きくなれば，作用静電容量の値は\( \ \fbox {　 （ウ） 　} \ \)なる。

作用静電容量を無視できない中距離送電線路では，作用静電容量によるアドミタンスを\( \ 1 \ \)か所又は\( \ 2 \ \)か所にまとめる\( \ \fbox {　 （エ） 　} \ \)定数回路が近似計算に用いられる。このとき，送電端側と受電端側の\( \ 2 \ \)か所にアドミタンスをまとめる回路を\( \ \fbox {　 （オ） 　} \ \)形回路という。

上記の記述中の空白箇所(ア)～(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 　漏れ　 & 　交流　 & 　小さく　 & 　集中　 & 　\mathrm {\pi }　 \\
\hline
(2) & 　漏れ　 & 　交流　 & 　大きく　 & 　集中　 & 　\mathrm {\pi }　 \\
\hline
(3) & 　伝達　 & 　直流　 & 　小さく　 & 　集中　 & 　\mathrm {T}　 \\
\hline
(4) & 　漏れ　 & 　直流　 & 　大きく　 & 　分布　 & 　\mathrm {T}　 \\
\hline
(5) & 　伝達　 & 　直流　 & 　小さく　 & 　分布　 & 　\mathrm {\pi }　 \\
\hline
\end{array}
\]

【ワンポイント解説】

架空送電線路の線路定数は，電線の太さ，長さ，配置，種類等の影響を受け，距離が短ければ線路定数も十分小さくなるので無視することができますが，距離が長くなるとその影響を無視できなくなります。
本問は，内容としては標準的な問題ですが，選択肢が若干迷いやすい問題で，十分な知識があっても間違える可能性がある問題と言えると思います。

1.送電線の線路定数
①線路抵抗
電線の抵抗率を\( \ \rho \ \mathrm {[\Omega \cdot {mm}^{2} ／ m ]} \ \)，電線の長さを\( \ l \ \mathrm {[m]} \ \)，断面積を\( \ S \ \mathrm {[{mm}^{2}]} \ \)とすると，線路抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R &=&\frac {\rho l}{S} \\[ 5pt ] \end{eqnarray}
\] で求められます。

②作用インダクタンス
線間距離\( \ D \ \mathrm {[m]} \ \)，電線半径\( \ r \ \mathrm {[m]} \ \)の送電線の作用インダクタンス\( \ L \ \mathrm {[mH/km]} \ \)は，
\[
\begin{eqnarray}
L &=&0.05+0.4605 \log_{10}\frac {D}{r} \\[ 5pt ] \end{eqnarray}
\] で求められます。したがって，線間距離\( \ D \ \)と電線半径\( \ r \ \)の比\( \ D／r \ \)が大きくなると作用インダクタンス\( \ L \ \)も大きくなります。

※　この式を暗記する必要はありません。

③作用静電容量
線間距離\( \ D \ \mathrm {[m]} \ \)，電線半径\( \ r \ \mathrm {[m]} \ \)の送電線の作用静電容量\( \ C \ \mathrm {[\mu F/km]} \ \)は，
\[
\begin{eqnarray}
C &=&\frac {0.02413}{\displaystyle \log_{10}\frac {D}{r}} \\[ 5pt ] \end{eqnarray}
\] で求められます。したがって，線間距離\( \ D \ \)と電線半径\( \ r \ \)の比\( \ D／r \ \)が大きくなると作用静電容量\( \ C \ \)は小さくなります。

※　この式を暗記する必要はありません。

④漏れコンダクタンス
がいし表面を流れる電流やコロナ損をコンダクタンスに換算したものですが，その値は非常に小さいので，一般に無視されます。

2.\( \ \mathrm {\pi } \ \)形回路と\( \ \mathrm {T} \ \)形回路
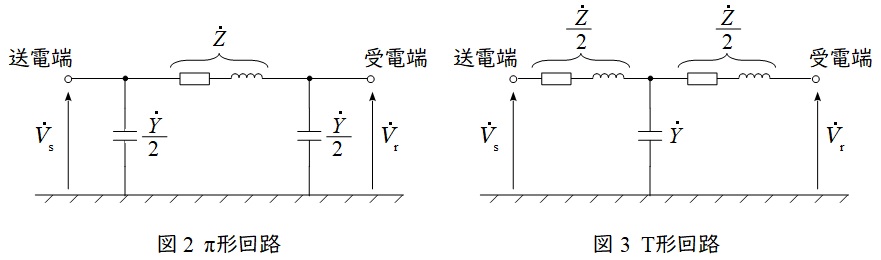
線路のこう長が長い長距離送電線では図1に示すような，各線路定数が直並列に分布している分布定数回路を使用しますが，こう長が\( \ 50～100 \ \mathrm {km} \ \)の中距離送電線では，図2や図3に示すような集中定数回路が使用されます。
集中定数回路には図2に示すような送電端側と受電端側の２か所にアドミタンスをまとめる\( \ \mathrm {\pi } \ \)形回路と中央部の１か所にアドミタンスをまとめる\( \ \mathrm {T} \ \)形回路があります。

【関連する「電気の神髄」記事】

　　往復導体の作用インダクタンス
　　円筒導体の静電容量
　　四端子定数のまとめ

【解答】

解答：(1)
(ア)
ワンポイント解説「1.送電線の線路定数」の通り，架空送電線路にはがいし表面を流れる電流やコロナ損をコンダクタンスに換算した漏れコンダクタンスがあります。

(イ)
表皮効果とは交流特有の現象であり，周波数の増加に伴い電線導体内の電流分布が表面に偏る現象のことで，中心部に電流が流れなくなることから，その抵抗値は大きくなります。

(ウ)
ワンポイント解説「1.送電線の線路定数」の通り，線間距離\( \ D \ \)と電線半径\( \ r \ \)の比\( \ D／r \ \)が大きくなると作用静電容量\( \ C \ \)は小さくなります。

(エ)
ワンポイント解説「2.\( \ \mathrm {\pi } \ \)形回路と\( \ \mathrm {T} \ \)形回路」の通り，中距離送電線路では，作用静電容量によるアドミタンスを\( \ 1 \ \)か所又は\( \ 2 \ \)か所にまとめる集中定数回路が近似計算として使用されます。

(オ)
ワンポイント解説「2.\( \ \mathrm {\pi } \ \)形回路と\( \ \mathrm {T} \ \)形回路」の通り，送電端側と受電端側の２か所にアドミタンスをまとめる回路を\( \ \mathrm {\pi } \ \)形回路と言います。