《電力》〈送電〉[H24:問10]送電線での送電損失に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

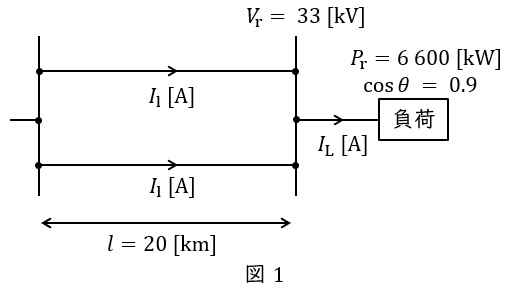
こう長\( \ 20 \ \mathrm {[km]} \ \)の三相\( \ 3 \ \)線式\( \ 2 \ \)回線の送電線路がある。受電端で\( \ 33 \ \mathrm {[kV]} \ \)，\( \ 6600 \ \mathrm {[kW]} \ \)，力率\( \ 0.9 \ \)の三相負荷に供給する場合，受電端電力に対する送電損失を\( \ 5 \ \mathrm {[％]} \ \)以下にするための電線の最小断面積\( \ \mathrm {[{mm}^{2}]} \ \)の値として，計算値が最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，使用電線は，断面積\( \ 1 \ \mathrm {[{mm}^{2}]} \ \)，長さ\( \ 1 \ \mathrm {[m]} \ \)当たりの抵抗を\( \ \displaystyle \frac {1}{35}\mathrm {[\Omega ]} \ \)とし，その他の条件は無視する。

　(1)　\(14.3\)　　(2)　\(23.4\)　　(3)　\(24.7\)　　(4)　\(42.8\)　　(5)　\(171\)　

【ワンポイント解説】

三相\( \ 3 \ \)線式で\( \ 2 \ \)回線であること，抵抗率の公式を使用すること等かなりの計算力を要する問題で\( \ 2 \ \)種の二次試験に出題されても良いようなレベルの問題と言えます。一つ一つの計算は非常に重要なものばかりなので，確実に理解するようにしましょう。

1.三相\( \ 3 \ \)線式線路の有効電力\( \ P \ \)
三相\( \ 3 \ \)線式の送電線の線間電圧が\( \ V \ \)，線電流が\( \ I \ \)，電圧と電流の力率が\( \ \cos \theta \ \)であるとき，送電電力\( \ P \ \)は，
\[
\begin{eqnarray}
P &=&\sqrt {3}VI\cos \theta \\[ 5pt ] \end{eqnarray}
\] となります。

2.抵抗率\( \ \rho \ \)
送電線の断面積\( \ 1 \ \mathrm {[{m}^{2}]} \ \)及び長さ\( \ 1 \ \mathrm {[m]} \ \)当たりの抵抗値\( \ \rho \ \mathrm {[\Omega \cdot m]} \)が与えられている時，断面積\( \ S \ \mathrm {[{m}^{2}]} \ \)，長さ\( \ l \ \mathrm {[m]} \ \)の送電線の抵抗\( \ R \ \mathrm {[\Omega]} \)の大きさは，
\[
\begin{eqnarray}
R &=&\frac {\rho l}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
題意より，受電端での電圧\( \ V_{\mathrm {r}}=33 \ \mathrm {[kV]} \ \)，電力\( \ P_{\mathrm {r}}=6600 \ \mathrm {[kW]} \ \)，力率\( \ \cos \theta =0.9 \ \)であるから，三相負荷を流れる電流\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \)は，ワンポイント解説「1.三相\( \ 3 \ \)線式の有効電力\( \ P \ \)」より，
\[
\begin{eqnarray}
P_{\mathrm {r}} &=&\sqrt {3}V_{\mathrm {r}}I_{\mathrm {L}}\cos \theta \\[ 5pt ] I_{\mathrm {L}} &=&\frac {P_{\mathrm {r}}}{\sqrt {3}V_{\mathrm {r}}\cos \theta } \\[ 5pt ] &=&\frac {6 \ 600\times 10^{3}}{\sqrt {3}\times 33\times 10^{3}\times 0.9 } \\[ 5pt ] &≒&128.3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] である。したがって，送電線\( \ 1 \ \)回線当たりの電流の大きさ\( \ I_{\mathrm {l}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {l}} &=&\frac {I_{\mathrm {L}}}{2} \\[ 5pt ] &=&\frac {128.3}{2} \\[ 5pt ] &≒&64.15 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。また，送電線\( \ 1 \ \)線当たりの抵抗値\( \ R \ \mathrm {[\Omega ]} \ \)は，断面積を\( \ S \ \mathrm {[{mm}^{2}]} \ \)とすると，ワンポイント解説「2.抵抗率\( \ \rho \ \)」より，
\[
\begin{eqnarray}
R &=&\frac {\rho l}{S} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{35} \times 20\times 10^{3}}{S} \\[ 5pt ] &≒&\frac {571.4}{S} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，送電線の損失\( \ P_{\mathrm {l}} \ \mathrm {[kW]} \ \)は，三相\( \ 3 \ \)線式\( \ 2 \ \)回線であることに注意すると，
\[
\begin{eqnarray}
P_{\mathrm {l}} &=&2\times 3RI_{\mathrm {l}}^{2} \\[ 5pt ] &=&6\times \frac {571.4}{S} \times 64.15^{2} \\[ 5pt ] &≒&\frac {14 \ 110 \ 000}{S} \ \mathrm {[W]}　→　\frac {14 \ 110}{S} \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。題意より，この値が受電電力の\( \ 5 \ \mathrm {[％]} \ \)以下にならなければならないので，
\[
\begin{eqnarray}
P_{\mathrm {l}} &=&0.05 P_{\mathrm {r}} \\[ 5pt ] \frac {14 \ 110}{S}&=&0.05 \times 6 \ 600 \\[ 5pt ] \frac {14 \ 110}{S}&=&330 \\[ 5pt ] S&≒&42.8 \ \mathrm {[{mm}^{2}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。