Contents
【問題】
【難易度】★★★★☆(やや難しい)
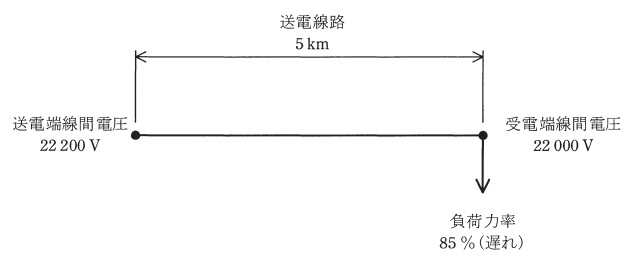
図のように,こう長\( \ \mathrm {5 \ km} \ \)の三相3線式1回線の送電線路がある。この送電線路における送電端線間電圧が\( \ \mathrm {22200 \ V} \ \),受電端線間電圧が\( \ \mathrm {22000 \ V} \ \),負荷力率が\( \ \mathrm {85 \ %} \ \)(遅れ)であるとき,負荷の有効電力\( \ \mathrm {[ kW ]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,\( \ \mathrm {1 \ km} \ \)当たりの電線\( \ 1 \ \)線の抵抗は\( \ \mathrm {0.182 \ \Omega } \ \),リアクタンスは\( \ \mathrm {0.355 \ \Omega } \ \)とし,その他の条件はないものとする。なお,本問では,送電端線間電圧と受電端線間電圧との位相角は小さいとして得られる近似式を用いて解答すること。
(1) \( \ 568 \ \) (2) \( \ 937 \ \) (3) \( \ 2189 \ \) (4) \( \ 3277 \ \) (5) \( \ 5675 \ \)
【ワンポイント解説】
送電線の電圧降下の近似式を覚えていないと解けない問題です。図を描いて導き出せるようにしても良いですが,基本的には暗記したい公式です。
1.三相3線式送電線路の電圧降下
送電線を流れる電流\( \ I \ \),抵抗\( \ R \ \),リアクタンス\( \ X \ \),負荷の位相角を\( \ \theta \ \)とすると,送電線の電圧降下\( \ \varepsilon \ \)は,送電端線間電圧と受電端線間電圧との位相角は十分に小さいと仮定すると
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta + X \sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.三相3線式の負荷の有効電力の公式
電圧\( \ V \ \),電流\( \ I \ \),力率\( \ \cos \theta \ \)とすると負荷の有効電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\sqrt {3}VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
解答:(3)
送電線の抵抗\( \ R \ \)とリアクタンス\( \ X \ \)は,
\[
\begin{eqnarray}
R&=&0.182 \times 5 \\[ 5pt ]
&=&0.910 \ \mathrm {[ \Omega ]} \\[ 5pt ]
X&=&0.355 \times 5 \\[ 5pt ]
&=&1.775 \ \mathrm {[ \Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,送電線の電圧降下\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&22200-22000 \\[ 5pt ]
&=& 200 \ \mathrm {[ V ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。力率\( \ \cos \theta =0.85 \ \)であるから,
\[
\begin{eqnarray}
\sin \theta &=& \sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=& \sqrt {1-0.85 ^{2}} \\[ 5pt ]
&≒& 0.52678 \\[ 5pt ]
\end{eqnarray}
\]
となる。送電線の電圧降下に関する近似式は,送電線に流れる電流を\( \ I \ \)とすると,
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta + X \sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
であるから,上式に各値を代入すると,
\[
\begin{eqnarray}
200 &=&\sqrt {3}I\left( 0.910\times 0.85 + 1.775 \times 0.52678 \right) \\[ 5pt ]
I&≒&67.584 \ \mathrm {[ A ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって,負荷の有効電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\sqrt {3}VI\cos \theta \\[ 5pt ]
&=&\sqrt {3}\times 22000 \times 67.584 \times 0.85 \\[ 5pt ]
&≒&2189000 \ \mathrm {[ W ]} → 2189 \ \mathrm {[ kW ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは