《法規》〈電気施設管理〉[H20:問12]複数の需要家に電力を供給する変電所の最大電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

ある変電所から供給される下表に示す需要家\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)がある。各需要家間の負荷の不等率を\( \ 1.2 \ \)とするとき，次の(a)及び(b)に答えよ。
\[
\begin{array}{|c|c|c|c|c|}
\hline
　需要家　 & 　負荷の設備容量　 & 　力　率　 & 　需要率　 & 　負荷率　 \\
& \mathrm {[kV\cdot A]} & & \mathrm {[％]} & \mathrm {[％]} \\
\hline
\mathrm {A} & 500 & 0.90 & 40 & 50 \\
\hline
\mathrm {B} & 200 & 0.85 & 60 & 60 \\
\hline
\mathrm {C} & 600 & 0.80 & 60 & 30 \\
\hline
\end{array}
\]

(a)　需要家\( \ \mathrm {A} \ \)の平均電力\( \ \mathrm {[kW]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 61.2 \ \)　　(2)　\( \ 86.4 \ \)　　(3)　\( \ 90 \ \)　　(4)　\( \ 180 \ \)　　(5)　\( \ 225 \ \)

(b)　変電所からみた合成最大需要電力\( \ \mathrm {[kW]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 198 \ \)　　(2)　\( \ 285 \ \)　　(3)　\( \ 325 \ \)　　(4)　\( \ 475 \ \)　　(5)　\( \ 684 \ \)

【ワンポイント解説】

需要家の平均需要電力と全体の合成最大電力を求める問題です。
よくあるパターンの問題ですが，誤答の選択肢が絶妙に作られていて，ちょっとしたミスを見逃してくれない印象の問題です。
定義式に沿って確実に計算していくようにして下さい。

1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
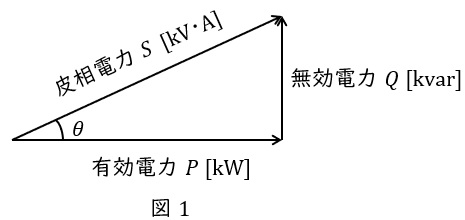
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図1のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図1において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

2.需要率，不等率，負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

②不等率（常に\( \ 1 \ \)以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {個々の最大需要電力の合計}{合成の最大需要電力} \\[ 5pt ] \end{eqnarray}
\]

③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(3)
需要家\( \ \mathrm {A} \ \)の設備容量\( \ S_{\mathrm {cA}}=500 \ \mathrm {[kV\cdot A]} \ \)，力率\( \ \cos \theta _{\mathrm {A}}=0.90 \ \)であるから，その有効電力\( \ P_{\mathrm {cA}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り，
\[
\begin{eqnarray}
P_{\mathrm {cA}}&=&S_{\mathrm {cA}}\cos \theta _{\mathrm {A}} \\[ 5pt ] &=&500\times 0.90 \\[ 5pt ] &=&450 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，需要家\( \ \mathrm {A} \ \)の最大需要電力\( \ P_{\mathrm {mA}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「2.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100 \\[ 5pt ] 40&=&\frac {P_{\mathrm {mA}}}{P_{\mathrm {cA}}}\times 100 \\[ 5pt ] P_{\mathrm {mA}}&=&P_{\mathrm {cA}}\times \frac {40}{100} \\[ 5pt ] &=&450\times \frac {40}{100} \\[ 5pt ] &=&180 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となるので，需要家\( \ \mathrm {A} \ \)の平均需要電力\( \ P_{\mathrm {aA}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「2.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100 \\[ 5pt ] 50&=&\frac {P_{\mathrm {aA}}}{P_{\mathrm {mA}}}\times 100 \\[ 5pt ] P_{\mathrm {aA}}&=&P_{\mathrm {mA}}\times \frac {50}{100} \\[ 5pt ] &=&180\times \frac {50}{100} \\[ 5pt ] &=&90 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
(a)と同様に，需要家\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)の設備容量の有効電力分\( \ P_{\mathrm {cB}} \ \mathrm {[kW]} \ \)及び\( \ P_{\mathrm {cC}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り，
\[
\begin{eqnarray}
P_{\mathrm {cB}}&=&S_{\mathrm {cB}}\cos \theta _{\mathrm {B}} \\[ 5pt ] &=&200\times 0.85 \\[ 5pt ] &=&170 \ \mathrm {[kW]} \\[ 5pt ] P_{\mathrm {cC}}&=&S_{\mathrm {cC}}\cos \theta _{\mathrm {C}} \\[ 5pt ] &=&600\times 0.80 \\[ 5pt ] &=&480 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となるので，需要家\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)の最大需要電力\( \ P_{\mathrm {mB}} \ \mathrm {[kW]} \ \)及び\( \ P_{\mathrm {mC}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「2.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100 \\[ 5pt ] 60&=&\frac {P_{\mathrm {mB}}}{P_{\mathrm {cB}}}\times 100 \\[ 5pt ] P_{\mathrm {mB}}&=&P_{\mathrm {cB}}\times \frac {60}{100} \\[ 5pt ] &=&170\times \frac {60}{100} \\[ 5pt ] &=&102 \ \mathrm {[kW]} \\[ 5pt ] 60&=&\frac {P_{\mathrm {mC}}}{P_{\mathrm {cC}}}\times 100 \\[ 5pt ] P_{\mathrm {mC}}&=&P_{\mathrm {cC}}\times \frac {60}{100} \\[ 5pt ] &=&480\times \frac {60}{100} \\[ 5pt ] &=&288 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，各需要家間の不等率が\( \ 1.2 \ \)であることから，変電所からみた合成最大需要電力\( \ P_{\mathrm {m}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「2.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
不等率&=&\frac {個々の最大需要電力の合計}{合成の最大需要電力} \\[ 5pt ] 1.2&=&\frac {P_{\mathrm {mA}}+P_{\mathrm {mB}}+P_{\mathrm {mC}}}{P_{\mathrm {m}}} \\[ 5pt ] P_{\mathrm {m}}&=&\frac {P_{\mathrm {mA}}+P_{\mathrm {mB}}+P_{\mathrm {mC}}}{1.2} \\[ 5pt ] &=&\frac {180+102+288}{1.2} \\[ 5pt ] &=&475 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。