Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
図に示すような,相電圧\( \ {\dot E}_{\mathrm {R}} \ \mathrm {[V]} \ \),\( \ {\dot E}_{\mathrm {S}} \ \mathrm {[V]} \ \),\( \ {\dot E}_{\mathrm {T}} \ \mathrm {[V]} \ \),角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)の対称三相\( \ 3 \ \)線式高圧電路があり,変圧器の中性点は非接地方式とする。電路の一相当たりの対地静電容量を\( \ C \ \mathrm {[F]} \ \)とする。
この電路の\( \ \mathrm {R} \ \)相のみが絶縁抵抗値\( \ R_{\mathrm {G}} \ \mathrm {[\Omega ]} \ \)に低下した。このとき,次の(a)及び(b)の問に答えよ。
ただし,上記以外のインピーダンスは無視するものとする。
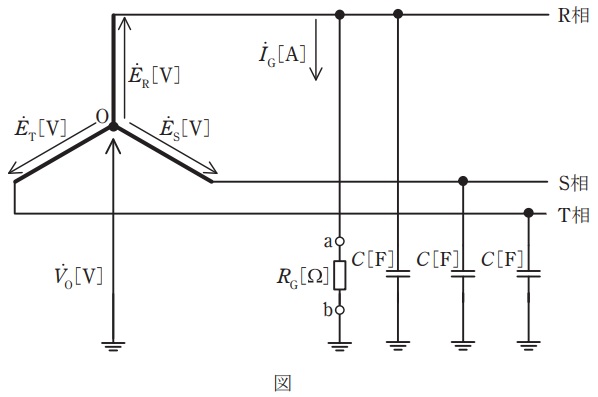
(a) 次の文章は,絶縁抵抗\( \ R_{\mathrm {G}} \ \mathrm {[\Omega ]} \ \)を流れる電流\( \ {\dot I}_{\mathrm {G}} \ \mathrm {[A]} \ \)を求める記述である。
\( \ R_{\mathrm {G}} \ \)を取り除いた場合
\( \ \mathrm {a-b} \ \)間の電圧\( \ {\dot V}_{\mathrm {ab}}= \ \fbox { (ア) } \ \)
\( \ \mathrm {a-b} \ \)間より見たインピーダンス\( \ {\dot Z}_{\mathrm {ab}} \ \)は,変圧器の内部インピーダンスを無視すれば,\( \ {\dot Z}_{\mathrm {ab}}= \ \fbox { (イ) } \ \)となる。
ゆえに,\( \ R_{\mathrm {G}} \ \)を接続したとき,\( \ R_{\mathrm {G}} \ \)に流れる電流\( \ {\dot I}_{\mathrm {G}} \ \)は,次式となる。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {G}}&=&\frac {{\dot V}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+R_{\mathrm {G}}}= \ \fbox { (ウ) } \ \\[ 5pt ]
\end{eqnarray}
\]
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& (ア) & (イ) & (ウ) \\
\hline
(1) & {\dot E}_{\mathrm {R}} & \displaystyle \frac {1}{\mathrm {j}3\omega C} & \displaystyle \frac {\mathrm {j}3\omega C{\dot E}_{\mathrm {R}}}{1+\mathrm {j}3\omega CR_{\mathrm {G}}} \\
\hline
(2) & \sqrt {3}{\dot E}_{\mathrm {R}} & -\mathrm {j}3\omega C & \displaystyle \frac {-\mathrm {j}3\omega C{\dot E}_{\mathrm {R}}}{1-\mathrm {j}3\omega CR_{\mathrm {G}}} \\
\hline
(3) & {\dot E}_{\mathrm {R}} & \displaystyle \frac {3}{\mathrm {j}\omega C} & \displaystyle \frac {\mathrm {j}\omega C{\dot E}_{\mathrm {R}}}{3+\mathrm {j}\omega CR_{\mathrm {G}}} \\
\hline
(4) & \sqrt {3}{\dot E}_{\mathrm {R}} & \displaystyle \frac {1}{\mathrm {j}3\omega C} & \displaystyle \frac {{\dot E}_{\mathrm {R}}}{1-\mathrm {j}3\omega CR_{\mathrm {G}}} \\
\hline
(5) & {\dot E}_{\mathrm {R}} & \mathrm {j}3\omega C & \displaystyle \frac {{\dot E}_{\mathrm {R}}}{1+\mathrm {j}3\omega CR_{\mathrm {G}}} \\
\hline
\end{array}
\]
(b) 次の文章は,変圧器の中性点\( \ \mathrm {O} \ \)点に現れる電圧\( \ {\dot V}_{\mathrm {O}} \ \mathrm {[V]} \ \)を求める記述である。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {O}}= \ \fbox { (エ) } \ +R_{\mathrm {G}}{\dot I}_{\mathrm {G}} \\[ 5pt ]
ゆえに{\dot V}_{\mathrm {O}}= \ \fbox { (オ) } \ \\[ 5pt ]
\end{eqnarray}
\]
上記の記述中の空白箇所(エ)及び(オ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& (エ) & (オ) \\
\hline
(1) & -{\dot E}_{\mathrm {R}} & \displaystyle \frac {-{\dot E}_{\mathrm {R}}}{1+\mathrm {j}3\omega CR_{\mathrm {G}}} \\
\hline
(2) & {\dot E}_{\mathrm {R}} & \displaystyle \frac {{\dot E}_{\mathrm {R}}}{1-\mathrm {j}3\omega CR_{\mathrm {G}}} \\
\hline
(3) & -{\dot E}_{\mathrm {R}} & \displaystyle \frac {-{\dot E}_{\mathrm {R}}}{1-\mathrm {j}3\omega CR_{\mathrm {G}}} \\
\hline
(4) & {\dot E}_{\mathrm {R}} & \displaystyle \frac {{\dot E}_{\mathrm {R}}}{1+\mathrm {j}3\omega CR_{\mathrm {G}}} \\
\hline
(5) & {\dot E}_{\mathrm {R}} & \displaystyle \frac {-{\dot E}_{\mathrm {R}}}{1-\mathrm {j}3\omega CR_{\mathrm {G}}} \\
\hline
\end{array}
\]
【ワンポイント解説】
配電線路において,一線の線路抵抗が低下したときの線路計算を行う問題です。
テブナンの定理を用いて三相回路を解く理論科目のような問題ですが,解法がかなりパターン化されているので,等価回路等も含め覚えてしまっても良いかもしれません。
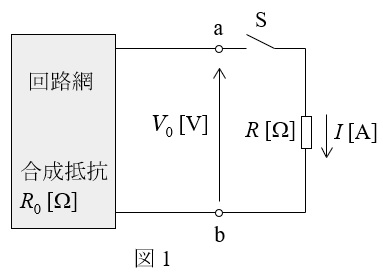
1.テブナンの定理
下図のような回路において,端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \),端子\( \ \mathrm {a-b} \ \)から電源側をみた合成抵抗を\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)とする(ただし,電圧源は短絡,電流源は開放する)と,図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流の大きさ\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
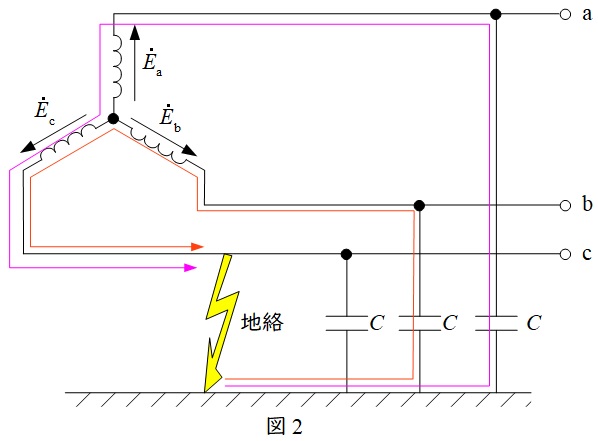
2.配電線路での\( \ 1 \ \)線地絡事故発生時の等価回路
三相\( \ 3 \ \)線式配電線路で\( \ 1 \ \)線地絡事故が発生した場合の様子を図2に示します。
地絡点にテブナンの定理を適用すると,地絡点からみた合成インピーダンス\( \ Z_{0} \ \)は,図に示すように\( \ 3 \ \)個の静電容量\( \ C \ \)の並列回路であるため,
\[
\begin{eqnarray}
Z_{0}&=&\frac {1}{\mathrm {j}2\pi f\cdot 3C} \\[ 5pt ]
\end{eqnarray}
\]
となり,開放電圧\( \ V \ \)は通常時の電圧となるので,三相平衡であるとすれば,
\[
\begin{eqnarray}
V&=&E_{\mathrm {c}}=E \\[ 5pt ]
\end{eqnarray}
\]
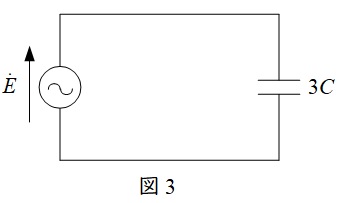
となります。したがって,完全地絡したときの等価回路は図3のようになります。
【解答】
(a)解答:(1)
(ア)
\( \ R_{\mathrm {G}} \ \)を取り除いた場合,三相平衡状態と同じ状態であるから,\( \ {\dot V}_{\mathrm {O}}=0 \ \mathrm {[V]} \ \)となるので,\( \ \mathrm {a-b} \ \)間の電圧\( \ {\dot V}_{\mathrm {ab}}= {\dot E}_{\mathrm {R}} \ \mathrm {[V]} \ \)と求められる。
(イ)
ワンポイント解説「2.配電線路での\( \ 1 \ \)線地絡事故発生時の等価回路」の通り,\( \ \mathrm {a-b} \ \)間からみたインピーダンス\( \ {\dot Z}_{\mathrm {ab}} \ \)は,\( \ 3 \ \)個の静電容量\( \ C \ \)の並列回路と考えれば良いため,\( \ \displaystyle \frac {1}{\mathrm {j}3\omega C} \ \)と求められる。
(ウ)
(ア),(イ)より,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {G}}&=&\frac {{\dot V}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+R_{\mathrm {G}}} \\[ 5pt ]
&=&\frac {{\dot E}_{\mathrm {R}}}{\displaystyle \frac {1}{\mathrm {j}3\omega C}+R_{\mathrm {G}}} \\[ 5pt ]
&=&\frac {{\dot E}_{\mathrm {R}}}{\displaystyle \frac {1+\mathrm {j}3\omega CR_{\mathrm {G}}}{\mathrm {j}3\omega C}} \\[ 5pt ]
&=&\frac {\mathrm {j}3\omega C{\dot E}_{\mathrm {R}}}{1+\mathrm {j}3\omega CR_{\mathrm {G}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(1)
(エ)
\( \ {\dot V}_{\mathrm {O}} \ \mathrm {[V]} \ \),\( \ {\dot E}_{\mathrm {R}} \ \mathrm {[V]} \ \),\( \ R_{\mathrm {G}} \ \mathrm {[\Omega ]} \ \)の閉回路について,キルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {O}} +{\dot E}_{\mathrm {R}} &=&R_{\mathrm {G}}{\dot I}_{\mathrm {G}} \\[ 5pt ]
{\dot V}_{\mathrm {O}}&=& -{\dot E}_{\mathrm {R}} +R_{\mathrm {G}}{\dot I}_{\mathrm {G}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(オ)
(エ)解答式に(ウ)解答式を代入すると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {O}}&=& -{\dot E}_{\mathrm {R}} +R_{\mathrm {G}}{\dot I}_{\mathrm {G}} \\[ 5pt ]
&=& -{\dot E}_{\mathrm {R}} +R_{\mathrm {G}}\cdot \frac {\mathrm {j}3\omega C{\dot E}_{\mathrm {R}}}{1+\mathrm {j}3\omega CR_{\mathrm {G}}} \\[ 5pt ]
&=& \frac {-{\dot E}_{\mathrm {R}}\left( 1+\mathrm {j}3\omega CR_{\mathrm {G}}\right) +\mathrm {j}3\omega CR_{\mathrm {G}}{\dot E}_{\mathrm {R}}}{1+\mathrm {j}3\omega CR_{\mathrm {G}}} \\[ 5pt ]
&=& \frac {-{\dot E}_{\mathrm {R}}-\mathrm {j}3\omega CR_{\mathrm {G}}{\dot E}_{\mathrm {R}} +\mathrm {j}3\omega CR_{\mathrm {G}}{\dot E}_{\mathrm {R}}}{1+\mathrm {j}3\omega CR_{\mathrm {G}}} \\[ 5pt ]
&=& \frac {-{\dot E}_{\mathrm {R}}}{1+\mathrm {j}3\omega CR_{\mathrm {G}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは