《法規》〈電気設備技術基準〉[R05上:問12]Ｂ種接地工事の抵抗値及び常時流れる電流に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

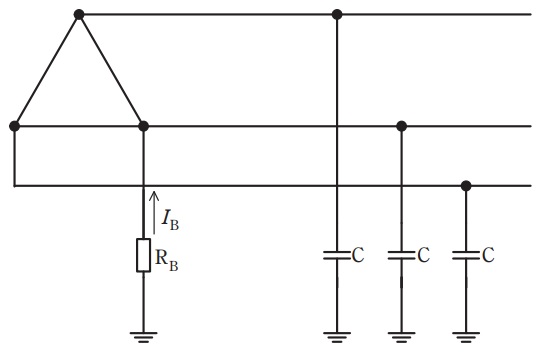
図は三相\( \ 3 \ \)線式高圧電路に変圧器で結合された変圧器低圧側電路を示したものである。低圧側電路の一端子には\( \ \mathrm {B} \ \)種接地工事が施されている。この電路の一相当たりの対地静電容量を\( \ \mathrm {C} \ \)とし接地抵抗を\( \ \mathrm {R}_{\mathrm {B}} \ \)とする。

低圧側電路の線間電圧\( \ 200 \ \mathrm {V} \ \)，周波数\( \ 50 \ \mathrm {Hz} \ \)，対地静電容量\( \ \mathrm {C} \ \)は\( \ 0.1 \ \mathrm {\mu F} \ \)として，次の(a)及び(b)の問に答えよ。

ただし，

(ア)　変圧器の高圧電路の\( \ 1 \ \)線地絡電流は\( \ 5 \ \mathrm {A} \ \)とする。

(イ)　高圧側電路と低圧側電路との混触時に低圧電路の対地電圧が\( \ 150 \ \mathrm {V} \ \)を超えた場合は\( \ 1.3 \ \)秒で自動的に高圧電路を遮断する装置が設けられているものとする。

(a)　変圧器に施された，接地抵抗\( \ \mathrm {R}_{\mathrm {B}} \ \)の抵抗値について「電気設備技術基準の解釈」で許容されている上限の抵抗値\( \ \mathrm {[\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 20 \ \)　　(2)　\( \ 30 \ \)　　(3)　\( \ 40 \ \)　　(4)　\( \ 60 \ \)　　(5)　\( \ 100 \ \)　　

(b)　接地抵抗\( \ \mathrm {R}_{\mathrm {B}} \ \)の抵抗値を\( \ 10 \ \Omega \ \)としたときに，\( \ \mathrm {R}_{\mathrm {B}} \ \)に常時流れる電流\( \ I_{\mathrm {B}} \ \)の値\( \ \mathrm {[mA]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，記載以外のインピーダンスは無視するものとする。

　(1)　\( \ 11 \ \)　　(2)　\( \ 19 \ \)　　(3)　\( \ 33 \ \)　　(4)　\( \ 65 \ \)　　(5)　\( \ 192 \ \)　　

【ワンポイント解説】

\( \ \mathrm {B} \ \)種接地工事の抵抗値及び常時流れる電流を求める問題です。
(a)は非常によく出題される計算問題，(b)は少し回路計算のテクニックが必要となる問題です。合格のためには(a)は絶対に間違えないようにしましょう。
本問は令和元年問13からの再出題となります。

1.テブナンの定理
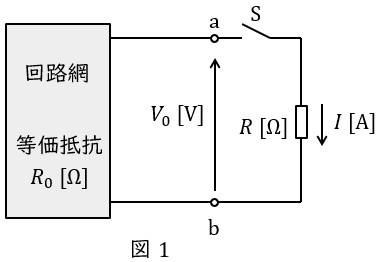
図1のような回路において，端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \)，端子\( \ \mathrm {a-b} \ \)から電源側をみた合成抵抗を\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)とする（ただし，電圧源は短絡，電流源は開放する）と，図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流の大きさ\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ] \end{eqnarray}
\] で求められます。この関係は抵抗のみでなく，リアクタンスにも適用可能です。

【解答】

(a)解答：(4)
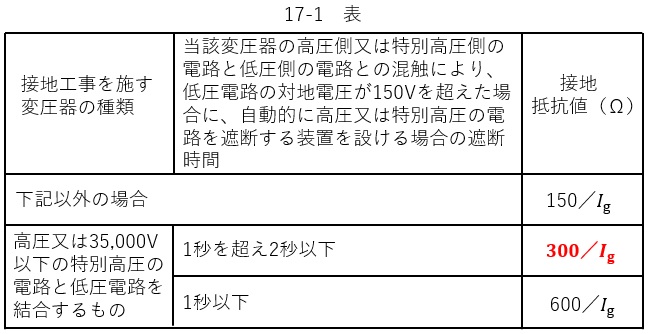
電気設備技術基準の解釈第17条第2項17-1表の通り，変圧器の高圧電路の\( \ 1 \ \)線地絡電流は\( \ 5 \ \mathrm {A} \ \)で，高圧側電路と低圧側電路との混触時に低圧電路の対地電圧が\( \ 150 \ \mathrm {V} \ \)を超えた場合は\( \ 1.3 \ \)秒で自動的に高圧電路を遮断する装置が設けられているので，接地抵抗値\( \ \mathrm {R}_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
\mathrm {R}_{\mathrm {B}} &=&\frac {300}{I_{\mathrm {g}}}\\[ 5pt ] &=&\frac {300}{5} \\[ 5pt ] &=&60 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
ワンポイント解説「1.テブナンの定理」の通り，接地抵抗\( \ \mathrm {R}_{\mathrm {B}} \ \)を切り離したときの開放電圧\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \)は，一方は端子電圧がかかり，もう一方は接地されているので，
\[
\begin{eqnarray}
V_{\mathrm {0}} &=&\frac {200}{\sqrt {3}}\\[ 5pt ] &≒&115.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。電圧源を短絡したときの\( \ \mathrm {R}_{\mathrm {B}} \ \)からみた等価インピーダンス（リアクタンス）\( \ X_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)は３つの対地静電容量\( \ \mathrm {C} \ \)の並列回路なので，
\[
\begin{eqnarray}
X_{\mathrm {0}} &=&\frac {1}{2\pi f \cdot 3\mathrm {C}}\\[ 5pt ] &=&\frac {1}{2\pi \times 50\times 3\times 0.1\times 10^{-6}}\\[ 5pt ] &≒&10 \ 610 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
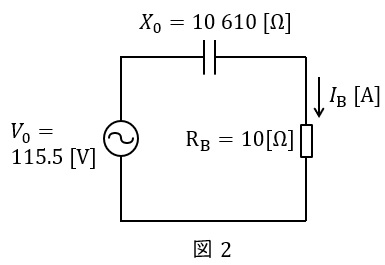
\] となる。よって，テブナンの定理の等価回路は図2のようになり，\( \ \mathrm {R}_{\mathrm {B}} \ \)に常時流れる電流\( \ I_{\mathrm {B}} \ \mathrm {[mA]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {B}} &=&\frac {V_{\mathrm {0}}}{\sqrt {\mathrm {R}_{\mathrm {B}}^{2}+ X_{\mathrm {0}}^{2}}}\\[ 5pt ] &=&\frac {115.5}{\sqrt {10^{2}+10610 ^{2}}}\\[ 5pt ] &≒&\frac {115.5}{10610}\\[ 5pt ] &≒&0.011 \ \mathrm {[A]}　→　11 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

＜電気設備技術基準の解釈第17条(抜粋)＞
\( \ \mathrm {A} \ \)種接地工事は、次の各号によること。
一　接地抵抗値は、\( \ 10 \ \mathrm {\Omega } \ \)以下であること。

2　\( \ \mathrm {B} \ \)種接地工事は、次の各号によること。
一　接地抵抗値は、17-1表に規定する値以下であること。

3　\( \ \mathrm {C} \ \)種接地工事は、次の各号によること。
一　接地抵抗値は、\( \ 10 \ \mathrm {\Omega } \ \)（低圧電路において、地絡を生じた場合に\( \ 0.5 \ \)秒以内に当該電路を自動的に遮断する装置を施設するときは、\( \ 500 \ \mathrm {\Omega } \ \)）以下であること。

4　\( \ \mathrm {D} \ \)種接地工事は、次の各号によること。
一　接地抵抗値は、\( \ 100 \ \mathrm {\Omega } \ \)（低圧電路において、地絡を生じた場合に\( \ 0.5 \ \)秒以内に当該電路を自動的に遮断する装置を施設するときは、\( \ 500 \ \mathrm {\Omega } \ \)）以下であること。