《法規》〈電気施設管理〉[R07上:問12]負荷設備から配電系統へ流出する第５調波電流に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

三相\( \ 3 \ \)線式配電線路から\( \ 6 \ 600 \ \mathrm {V} \ \)で受電している三相負荷設備がある。この負荷設備から配電系統へ流出する第\( \ 5 \ \)調波電流を算出するにあたり，次の(a)及び(b)に答えよ。

ただし，負荷設備は定格容量\( \ 500 \ \mathrm {kV\cdot A} \ \)で，力率改善用として\( \ 6 \ \mathrm {％} \ \)直列リアクトル付きコンデンサ設備が設置されており，この負荷設備から発生する第\( \ 5 \ \)調波電流は，負荷設備の定格電流に対し\( \ 15 \ \mathrm {％} \ \)とする。

また，受電点よりみた配電線路側の第\( \ n \ \)調波に対するインピーダンスは\( \ 10 \ \mathrm {MV\cdot A} \ \)基準で\( \ \mathrm {j}6\times n \ \mathrm {[％]} \ \)，コンデンサ設備のインピーダンスは\( \ 10 \ \mathrm {MV\cdot A} \ \)基準で\( \ \displaystyle \mathrm {j}50\times \left( 6 \times n -\frac {100}{n} \right) \ \mathrm {[％]} \ \)で表され，発生高調波は定電流源と見なせるものとし，次のような等価回路で表すことができる。

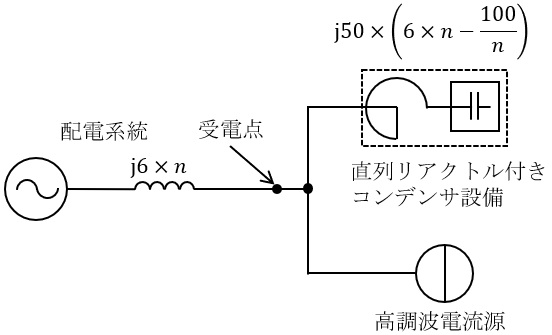
(a)　高調波発生機器から発生する第\( \ 5 \ \)調波電流の受電点電圧に換算した電流\( \ \mathrm {[A]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 1.3 \ \)　　(2)　\( \ 6.6 \ \)　　(3)　\( \ 11.4 \ \)　　(4)　\( \ 32.8 \ \)　　(5)　\( \ 43.7 \ \)

(b)　受電点から配電系統に流出する第\( \ 5 \ \)調波電流\( \ \mathrm {[A]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 1.2 \ \)　　(2)　\( \ 6.2 \ \)　　(3)　\( \ 10.8 \ \)　　(4)　\( \ 30.9 \ \)　　(5)　\( \ 41.2 \ \)

【ワンポイント解説】

負荷設備から配電系統へ流出する第\( \ 5 \ \)調波電流を求める問題です。
本問においては配電系統とコンデンサ設備のインピーダンスの導出式が与えられていますが，与えられなくても導出できるようになる必要があります。第\( \ 5 \ \)調波のインピーダンスがどうなるか理解しておくようにして下さい。
本問は平成18年問13からの再出題ですが，令和2年問13でも第5調波に関する問題が出題されていますので，合わせて学習することをお勧めします。

1.コイル，コンデンサのリアクタンス（理論及び電力科目）
コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのリアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ] &=&\mathrm {j}2\pi f L \\[ 5pt ] -\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&\frac {1}{\mathrm {j}2\pi f C}\left( \frac {1}{\mathrm {j}}=\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}}=-\mathrm {j}\right) \\[ 5pt ] \end{eqnarray}
\] で求められます。したがって，第\( \ 5 \ \)次高調波に対するリアクタンス\( \ X_{\mathrm {L5}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C5}} \ \mathrm {[\Omega ]} \ \)は，周波数が\( \ 5 \ \)倍となるので，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L5}}&=&\mathrm {j}2\pi \times 5f \times L \\[ 5pt ] &=&\mathrm {j}5 X_{\mathrm {L}} \\[ 5pt ] -\mathrm {j}X_{\mathrm {C5}}&=&\frac {1}{\mathrm {j}2\pi \times 5f \times C} \\[ 5pt ] &=&-\mathrm {j}\frac {X_{\mathrm {C}}}{5} \\[ 5pt ] \end{eqnarray}
\] となります。

2.分圧・分流の法則（理論科目）
①分圧の法則
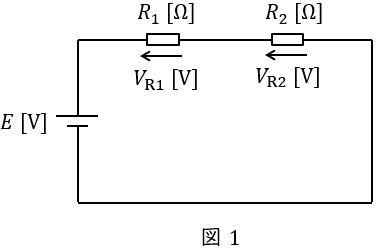
図1に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

②分流の法則
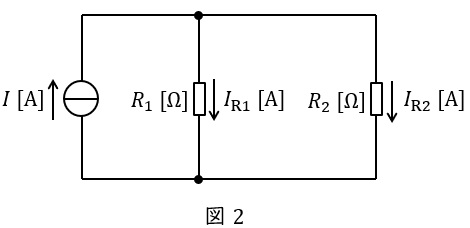
図2に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(2)
負荷設備の定格容量が\( \ P_{\mathrm {n}}=500 \ \mathrm {[kV\cdot A]} \ \)，定格電圧が\( \ V_{\mathrm {n}}=6 \ 600 \ \mathrm {[V]} \ \)であるから，定格電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {500\times 10^{3}}{\sqrt {3}\times 6 \ 600} \\[ 5pt ] &≒&43.74 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] あり，負荷設備から発生する第\( \ 5 \ \)調波電流\( \ I_{\mathrm {5}} \ \mathrm {[A]} \ \)は，負荷設備の定格電流に対し\( \ 15 \ \mathrm {％} \ \)なので，
\[
\begin{eqnarray}
I_{\mathrm {5}}&=&0.15I_{\mathrm {n}} \\[ 5pt ] &=&0.15\times 43.74 \\[ 5pt ] &≒&6.561　→　6.6 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
第\( \ 5 \ \)調波に対する配電系統のインピーダンス\( \ ％Z_{\mathrm {l}} \ \mathrm {[％]} \ \)及びコンデンサ設備のインピーダンス\( \ ％Z_{\mathrm {C}} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z_{\mathrm {l}}&=&\mathrm {j}6\times 5 \\[ 5pt ] &=&\mathrm {j}30 \ \mathrm {[％]} \\[ 5pt ] ％Z_{\mathrm {C}}&=&\mathrm {j}50\times \left( 6 \times 5 -\frac {100}{5} \right) \\[ 5pt ] &=&\mathrm {j}500 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となるので，受電点から配電系統に流出する第\( \ 5 \ \)調波電流\( \ I_{\mathrm {l5}} \ \mathrm {[A]} \ \)は，分流の法則より，
\[
\begin{eqnarray}
I_{\mathrm {l5}}&=&\frac {％Z_{\mathrm {C}}}{％Z_{\mathrm {l}}+％Z_{\mathrm {C}}}I_{\mathrm {5}} \\[ 5pt ] &=&\frac {\mathrm {j}500}{\mathrm {j}30+\mathrm {j}500}\times 6.561 \\[ 5pt ] &≒&6.2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。