《機械》〈同期機〉[H18:問3]三相同期発電機の短絡比に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

定格出力\( \ 5 \ \mathrm {[MV\cdot A]} \ \)，定格電圧\( \ 6.6 \ \mathrm {[kV]} \ \)，定格回転速度\( \ 1 \ 800 \ \mathrm {[{min}^{-1}]} \ \)の三相同期発電機がある。この発電機の同期インピーダンスが\( \ 7.26 \ \mathrm {[\Omega ]} \ \)のとき，短絡比の値として，正しいのは次のうちどれか。

　(1)　\( \ 0.14 \ \)　　(2)　\( \ 0.83 \ \)　　(3)　\( \ 1.0 \ \)　　(4)　\( \ 1.2 \ \)　　(5)　 \( \ 1.5 \ \)

【ワンポイント解説】

同期インピーダンスから短絡比を求める問題です。
様々な導出方法が考えられますが，三相短絡電流と定格電流の関係，短絡比と百分率インピーダンスの関係は覚えておいた方がよい公式となります。
両方の解法を紹介していますので，両方ともマスターしておくようにして下さい。

1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス（パーセントインピーダンス）\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 　(定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.同期発電機の無負荷飽和曲線と三相短絡曲線
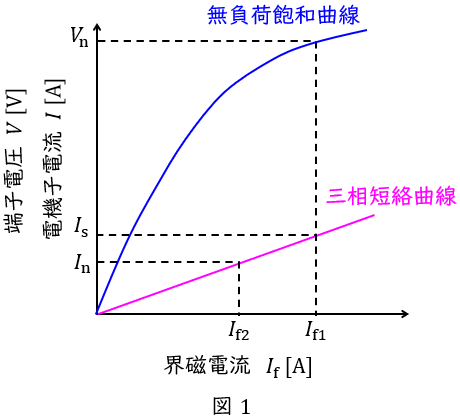
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。
無負荷飽和曲線は定格速度で無負荷で運転したときの界磁電流と端子電圧の関係，三相短絡曲線は電機子巻線の三相の出力端子を短絡し定格速度で運転したときの界磁電流と三相短絡電流の関係，を表したものです。
図中の\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)は定格電圧，\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は定格電流，三相短絡曲線は曲線ですが，ほぼ比例の直線と近似できます。
この時，\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は定格電圧時の三相短絡電流であり，短絡比\( \ K \ \)は，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.百分率インピーダンスと短絡比の関係
同期発電機の百分率同期インピーダンスが\( \ ％Z \ \mathrm {[％]} \ \)，短絡比が\( \ K \ \)であるとき，その関係は，
\[
\begin{eqnarray}
K&=&\frac {100}{％Z} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ] K&=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}\times 100}\times 100 \\[ 5pt ] &=&\frac {100}{％Z_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(4)
定格出力\( \ P_{n}=5 \ \mathrm {[MV\cdot A]} \ \)，定格電圧\( \ V_{n}=6.6 \ \mathrm {[kV]} \ \)より，定格電流\( \ I_{n} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{n} &=& \frac {P_{n}}{\sqrt {3}V_{n}} \\[ 5pt ] &=& \frac {5\times 10^{6}}{\sqrt {3}\times 6.6\times 10^{3}} \\[ 5pt ] &≒& 437.4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，同期インピーダンス\( \ Z_{s}=7.26 \ \mathrm {[\Omega ]} \ \)より，三相短絡電流\( \ I_{s} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{s} &=& \frac {\displaystyle \frac {V_{n}}{\sqrt {3}}}{Z_{s}} \\[ 5pt ] &=& \frac {\displaystyle \frac {6.6\times 10^{3}}{\sqrt {3}}}{7.26} \\[ 5pt ] &≒& 524.9 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，短絡比\( \ K \ \)は，ワンポイント解説「2.同期発電機の無負荷飽和曲線と三相短絡曲線」の通り，
\[
\begin{eqnarray}
K &=& \frac {I_{s}}{I_{n}} \\[ 5pt ] &=& \frac {524.9}{437.4} \\[ 5pt ] &≒& 1.20 \\[ 5pt ] \end{eqnarray}
\] と求められる。

［別解］
同期インピーダンス\( \ Z_{s}=7.26 \ \mathrm {[\Omega ]} \ \)より，百分率インピーダンス\( \ ％Z_{s} \ \mathrm {[％]} \ \)は，ワンポイント解説「1.オーム法からパーセントインピーダンス法への変換」の通り，
\[
\begin{eqnarray}
％Z_{s}&=&\frac {P_{n}Z_{s}}{V_{n}^{2}}\times 100 \\[ 5pt ] &=&\frac {5\times 10^{6}\times 7.26}{\left( 6.6\times 10^{3}\right) ^{2}}\times 100 \\[ 5pt ] &≒& 83.33 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となるので，短絡比\( \ K \ \)は，ワンポイント解説「3.百分率インピーダンスと短絡比の関係」の通り，
\[
\begin{eqnarray}
K&=&\frac {100}{％Z_{s}} \\[ 5pt ] &=&\frac {100}{83.33} \\[ 5pt ] &≒& 1.20 \\[ 5pt ] \end{eqnarray}
\] と求められる。