《機械》〈回転機〉[R3:問5]三相同期電動機の特性や構造に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，三相同期電動機に関する記述である。

三相同期電動機が負荷を担って回転しているとき，回転子磁極の位置と，固定子の三相巻線によって生じる回転磁界の位置との間には，トルクに応じた角度\( \ \delta \ \mathrm {[rad]} \ \)が発生する。この角度\( \ \delta \ \)を\( \ \fbox {　 （ア） 　} \ \)という。

回転子が円筒形で\( \ 2 \ \)極の三相同期電動機の場合，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は\( \ \delta \ \)が\( \ \fbox {　 （イ） 　} \ \mathrm {[rad]} \ \)のときに最大値になる。さらに\( \ \delta \ \)が大きくなると，トルクは減少して電動機は停止する。同期電動機が停止しない最大トルクを\( \ \fbox {　 （ウ） 　} \ \)という。

また，同期電動機の負荷が急変すると，\( \ \delta \ \)が変化し，新たな\( \ \delta ^{\prime } \ \)に落ち着こうとするが，回転子の慣性のために，\( \ \delta ^{\prime } \ \)を中心として周期的に変動する。これを\( \ \fbox {　 （エ） 　} \ \)といい，電源の電圧や周波数が変動した場合にも生じる。\( \ \fbox {　 （エ） 　} \ \)を抑制するには，始動巻線も兼ねる\( \ \fbox {　 （オ） 　} \ \)を設けたり，はずみ車を取り付けたりする。

上記の記述中の空白箇所(ア)～(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 　負荷角　 & 　\pi　 & 　脱出トルク　 & 　乱調　 & 　界磁巻線　 \\
\hline
(2) & 　力率角　 & 　\pi　 & 　制動トルク　 & 　同期外れ　 & 　界磁巻線　 \\
\hline
(3) & 　負荷角　 & 　\displaystyle \frac {\pi }{2}　 & 　脱出トルク　 & 　乱調　 & 　界磁巻線　 \\
\hline
(4) & 　力率角　 & 　\displaystyle \frac {\pi }{2}　 & 　制動トルク　 & 　同期外れ　 & 　制動巻線　 \\
\hline
(5) & 　負荷角　 & 　\displaystyle \frac {\pi }{2}　 & 　脱出トルク　 & 　乱調　 & 　制動巻線　 \\
\hline
\end{array}
\]

【ワンポイント解説】

同期電動機の特徴や構造に関する問題です。
各名称や現象は暗記するしかありませんが，力率角と負荷角の違いや制動巻線等は同期機特有の内容となるので，これらから正答を導き出せれば良いかと思います。

1.三相同期電動機の等価回路及びベクトル図
三相同期電動機の等価回路は，端子電圧\( \ \dot V \ \mathrm {[V]} \ \)（相電圧），誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)（相電圧），電機子電流\( \ \dot I \ \mathrm {[A]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)とすると，図1のようになります。ただし，電機子巻線抵抗は小さいものとします。

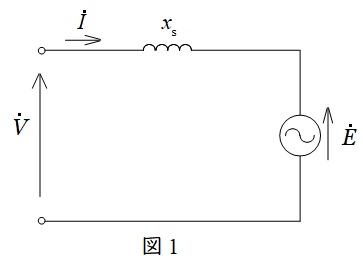
等価回路より，キルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
\dot V &=& \dot E+\mathrm {j}x_{\mathrm {s}}\dot I \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。
ここで，\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot I \ \mathrm {[A]} \ \)の力率角を\( \ \theta \ \mathrm {[rad]} \ \)とすると，ベクトル図は図2のように描くことができます。

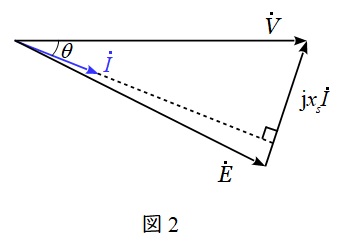
2.三相同期電動機の出力
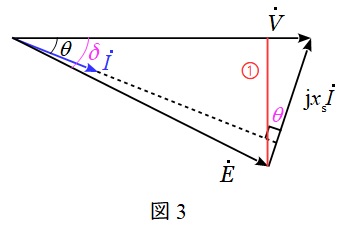
図3のように端子電圧\( \ \dot V \ \mathrm {[V]} \ \)と誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)の負荷角を\( \ \delta \ \mathrm {[rad]} \ \)とすると，
図3の①線を求める式より，
\[
\begin{eqnarray}
E \sin \delta &=& x_{\mathrm {s}}I\cos \theta \\[ 5pt ] I\cos \theta &=&\frac {E }{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] \end{eqnarray}
\] となるため，三相同期電動機の出力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=& 3VI\cos \theta \\[ 5pt ] &=& 3V\cdot \frac {E }{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] &=& \frac {3VE }{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] \end{eqnarray}
\] と求められます。したがって，出力\( \ P \ \mathrm {[W]} \ \)と負荷角\( \ \delta \ \mathrm {[rad]} \ \)の関係は図4のようになり，\( \ \displaystyle 0 \lt \delta \lt \frac {\pi }{2} \ \)のとき安定となり，\( \ \displaystyle \delta =\frac {\pi }{2} \ \mathrm {[rad]} \ \)のときのトルクを，脱出トルク（同期電動機が停止しない最大トルク）といいます。

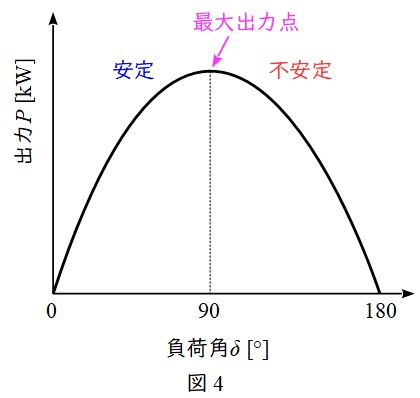
3.同期機の制動巻線
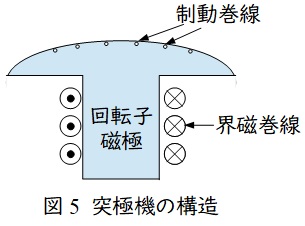
制動巻線は図5のように回転子鉄心の磁極の末端に設けられます。制動巻線の末端はかご形誘導電動機の二次巻線の端絡環のような形となっています。制動巻線の目的は以下の通りです。
①　負荷急変時，もしくは界磁磁束急変時の同期外れの防止
②　不平衡負荷運転状態で逆相電流が流れる際に発生する逆相回転磁界及び負荷電流のひずみによる高調波磁界を吸収する
③　誘導電動機と同様に始動させる（自己始動法）

【解答】

解答：(5)
(ア)
ワンポイント解説「1.三相同期電動機の等価回路及びベクトル図」及び「2.三相同期電動機の出力」の通り，\( \ \delta \ \mathrm {[rad]} \ \)は負荷角といいます。力率角は負荷における電圧\( \ \dot V \ \mathrm {[V]} \ \)と電流\( \ \dot I \ \mathrm {[A]} \ \)の位相差となります。

(イ)
トルク\( \ T \ \mathrm {[N\cdot m]} \ \)と出力\( \ P \ \mathrm {[W]} \ \)には，角速度\( \ \omega \ \mathrm {[rad/s]} \ \)とすると，
\[
\begin{eqnarray}
P &=&\omega T \\[ 5pt ] \end{eqnarray}
\] の関係があり，\( \ T \ \mathrm {[N\cdot m]} \ \)が最大となるのは出力\( \ P \ \mathrm {[W]} \ \)が最大となる\( \ \displaystyle \delta =\frac {\pi }{2} \ \mathrm {[rad]} \ \)となります。

(ウ)
同期電動機が停止しない最大トルクを脱出トルクといいます。

(エ)
負荷が急変すると，負荷角\( \ \delta \ \)が変化し，振動的に目的の負荷角に落ち着いていきます。これを乱調といいます。

(オ)
ワンポイント解説「3.同期機の制動巻線」の通り，乱調を抑制するには，始動巻線も兼ねる制動巻線を設けます。