Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
巻線形誘導電動機のトルク-回転速度曲線は,電源電圧及び\( \ \fbox { (ア) } \ \)が一定のとき,発生するトルクと回転速度との関係を表したものである。
この曲線は,ある滑りの値でトルクが最大となる特性を示す。このトルクを最大トルク又は\( \ \fbox { (イ) } \ \)トルクと呼んでいる。この最大トルクは\( \ \fbox { (ウ) } \ \)回路の抵抗には無関係である。
巻線形誘導電動機のトルクは\( \ \fbox { (ウ) } \ \)回路の抵抗と滑りの比に関係するので,\( \ \fbox { (ウ) } \ \)回路の抵抗が\( \ k \ \)倍になると,前と同じトルクが前の滑りの\( \ k \ \)倍の点で起こる。このような現象は\( \ \fbox { (エ) } \ \)と呼ばれ,巻線形誘導電動機の起動トルクの改善及び速度制御に広く用いられている。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 負 荷 & 臨 界 & 二 次 & 比例推移 \\
\hline
(2) & 電源周波数 & 停 動 & 一 次 & 二次励磁 \\
\hline
(3) & 負 荷 & 臨 界 & 一 次 & 比例推移 \\
\hline
(4) & 電源周波数 & 臨 界 & 二 次 & 二次励磁 \\
\hline
(5) & 電源周波数 & 停 動 & 二 次 & 比例推移 \\
\hline
\end{array}
\]
【ワンポイント解説】
巻線形誘導電動機におけるトルクと回転速度の関係を問う問題です。
電験でも計算問題や知識問題として何度も出題されている内容です。トルクを自力で導出できると理想ですが,試験時間は限られているためトルクの比例推移の関係は覚えておくようにして下さい。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \),回転子の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と定義されます。これを整理すると,
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ]
N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ]
&=&\left( 1-s \right) N_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
と同期速度から回転速度が導出できます。
3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \),二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \),出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。

4.巻線形誘導電動機のトルクの比例推移
三相誘導電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,
\[
\begin{eqnarray}
T &=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ 1≫s \ \)の時,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)以外の抵抗やリアクタンスは無視できるので,
\[
\begin{eqnarray}
T &≃& \frac {3V_{1}^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ]
\end{eqnarray}
\]
となり,トルクに対する変数は可変抵抗(外部抵抗が挿入可能)である二次抵抗\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)と滑り\( \ s \ \)のみであり,トルク\( \ T \ \mathrm {[N\cdot m]} \ \)を一定とすると,
\[
\begin{eqnarray}
\frac {r_{2}^{\prime }}{s} &=& 一定 \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
解答:(5)
(ア)
ワンポイント解説「4.巻線形誘導電動機のトルクの比例推移」の通り,三相誘導電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,
\[
\begin{eqnarray}
T &≃& \frac {3V_{1}^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ]
\end{eqnarray}
\]
となりますが,トルク-回転速度曲線は電源電圧\( \ V_{1} \ \)と電源周波数により決定される同期角速度\( \ \omega _{\mathrm {s}} \ \)が一定の条件で,トルクと滑り(回転速度)の関係を示したものとなります。
(イ)
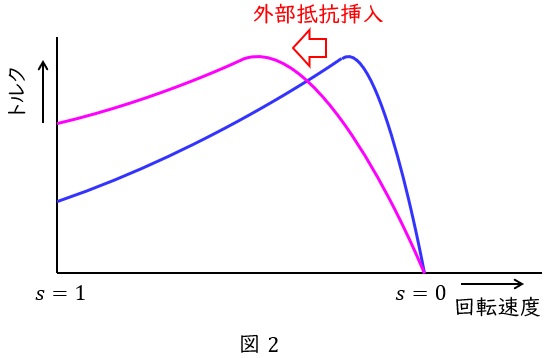
トルク-回転速度曲線は図2に示すような形であり,最大トルクのことを停動トルクとも呼びます。
(ウ)
ワンポイント解説「4.巻線形誘導電動機のトルクの比例推移」の通り,巻線形誘導電動機のトルクは二次回路の抵抗と滑りの比にほぼ比例します。
(エ)
ワンポイント解説「4.巻線形誘導電動機のトルクの比例推移」の通り,トルクが二次抵抗と滑りの比に比例する現象をトルクの比例推移といいます。





















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは