Contents
【問題】
【難易度】★★★★★(難しい)
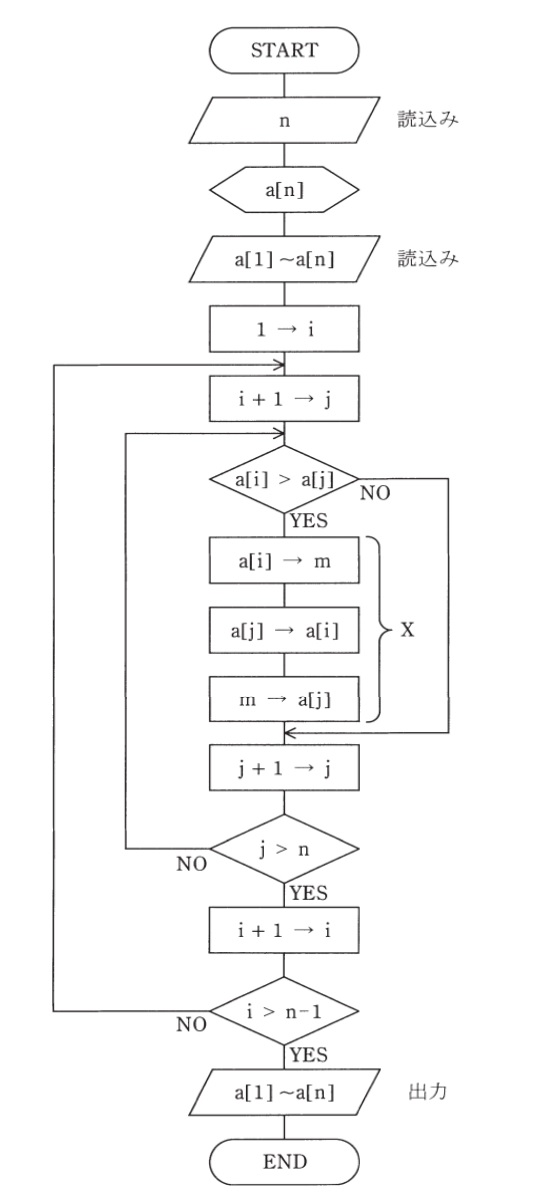
図のフローチャートで表されるアルゴリズムについて,次の(a)及び(b)の問に答えよ。変数は全て整数型とする。
このアルゴリズム実行時の読込み処理において,\( \ \mathrm {n}=5 \ \)とし,\( \ \mathrm {a}[1]=2 \ \),\( \ \mathrm {a}[2]=3 \ \),\( \ \mathrm {a}[3]=8 \ \),\( \ \mathrm {a}[4]=6 \ \),\( \ \mathrm {a}[5]=5 \ \)とする。
(a) 図のフローチャートで表されるアルゴリズムの機能を考えて,出力される\( \ \mathrm {a}[5] \ \)の値を求めよ。その値として正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 2 \ \) (2) \( \ 3 \ \) (3) \( \ 5 \ \) (4) \( \ 6 \ \) (5) \( \ 8 \ \)
(b) フローチャート中の\( \ \mathrm {X} \ \)で示される部分の処理は何回行われるか。正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 3 \ \) (2) \( \ 4 \ \) (3) \( \ 5 \ \) (4) \( \ 8 \ \) (5) \( \ 10 \ \)
【ワンポイント解説】
アルゴリズムの問題でパズルゲームを解いているような問題です。ただし,問題を解くのにかなりの時間を要する上,ケアレスミスも発生しやすい問題なので,90分しかない試験時間でこの問題は選択しない方が良いと思います。
【解答】
(a)解答:(5)
下記プログラムの青字の通り,出力される\( \ \mathrm {a}[5] \ \)は\( \ 8 \ \)となります。
(b)解答:(1)
下記プログラムの赤字の通り,\( \ \mathrm {X} \ \)の回数は3回です。
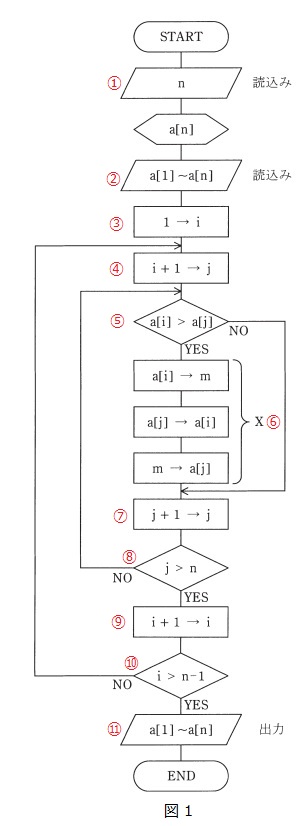
図1のように各プロセスに番号をつけ,アルゴリズムに沿って解いていきます。
①\( \ \mathrm {n} \ \)を「読込み」します。⇒\( \ \mathrm {n}=5 \ \)
②\( \ \mathrm {a}[1] \ ~ \ \mathrm {a}[\mathrm {n}] \ \)を「読込み」します。⇒\( \ \mathrm {a}[1]=2 \ \),\( \ \mathrm {a}[2]=3 \ \),\( \ \mathrm {a}[3]=8 \ \),\( \ \mathrm {a}[4]=6 \ \),\( \ \mathrm {a}[5]=5 \ \)
③\( \ \mathrm {i} \ \)を\( \ 1 \ \)とします。⇒\( \ \mathrm {i}=1 \ \)
④\( \ \mathrm {j} \ \)を\( \ \mathrm {i}+1 \ \)とします。⇒\( \ \mathrm {j}=2 \ \)
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[1]=2<\mathrm {a}[2]=3 \ \)なので\( \ \mathrm {NO} \ \)へ
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=3 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=3<\mathrm {n}=5 \ \)なので\( \ \mathrm {NO} \ \)へ
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[1]=2<\mathrm {a}[3]=8 \ \)なので\( \ \mathrm {NO} \ \)へ
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=4 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=4<\mathrm {n}=5 \ \)なので\( \ \mathrm {NO} \ \)へ
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[1]=2<\mathrm {a}[4]=6 \ \)なので\( \ \mathrm {NO} \ \)へ
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=5 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=5=\mathrm {n}=5 \ \)なので\( \ \mathrm {NO} \ \)へ
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[1]=2<\mathrm {a}[5]=5 \ \)なので\( \ \mathrm {NO} \ \)へ
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=6 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=6>\mathrm {n}=5 \ \)なので\( \ \mathrm {YES} \ \)へ
⑨\( \ \mathrm {i} \ \)を\( \ \mathrm {i}+1 \ \)とします。⇒\( \ \mathrm {i}=2 \ \)
⑩\( \ \mathrm {i}>\mathrm {n}-1 \ \)かどうかを確認します。⇒\( \ \mathrm {i}=2<\mathrm {n}-1=4 \ \)なので\( \ \mathrm {NO} \ \)へ
④\( \ \mathrm {j}\)を\( \ \mathrm {i}+1\)とします。⇒\( \ \mathrm {j}=3\)
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[2]=3<\mathrm {a}[3]=8 \ \)なので\( \ \mathrm {NO} \ \)へ
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=4 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=4<\mathrm {n}=5 \ \)なので\( \ \mathrm {NO} \ \)へ
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[2]=3<\mathrm {a}[4]=6 \ \)なので\( \ \mathrm {NO} \ \)へ
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=5 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=5=\mathrm {n}=5 \ \)なので\( \ \mathrm {NO} \ \)へ
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[2]=3<\mathrm {a}[5]=5 \ \)なので\( \ \mathrm {NO} \ \)へ
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=6 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=6>\mathrm {n}=5 \ \)なので\( \ \mathrm {YES} \ \)へ
⑨\( \ \mathrm {i} \ \)を\( \ \mathrm {i}+1 \ \)とします。⇒\( \ \mathrm {i}=3 \ \)
⑩\( \ \mathrm {i}>\mathrm {n}-1 \ \)かどうかを確認します。⇒\( \ \mathrm {i}=3<\mathrm {n}-1=4 \ \)なので\( \ \mathrm {NO} \ \)へ
④\( \ \mathrm {j} \ \)を\( \ \mathrm {i}+1 \ \)とします。⇒\( \ \mathrm {j}=4 \ \)
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[3]=8>\mathrm {a}[4]=6 \ \)なので\( \ \mathrm {YES} \ \)へ
⑥\( \ \mathrm {m} \ \)を\( \ \mathrm {a}[\mathrm {i}] \ \)として\( \ \mathrm {a}[\mathrm {i}] \ \)を\( \ \mathrm {a}[\mathrm {j}] \ \)として\( \ \mathrm {a}[\mathrm {j}] \ \)を\( \ \mathrm {m} \ \)とします⇒\( \ \mathrm {a}[3]=6 \ \),\( \ \mathrm {a}[4]=8 \ \)
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=5 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=5=\mathrm {n}=5 \ \)なので\( \ \mathrm {NO} \ \)へ
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[3]=6>\mathrm {a}[5]=5 \ \)なので\( \ \mathrm {YES} \ \)へ
⑥\( \ \mathrm {m} \ \)を\( \ \mathrm {a}[\mathrm {i}] \ \)として\( \ \mathrm {a}[\mathrm {i}] \ \)を\( \ \mathrm {a}[\mathrm {j}] \ \)として\( \ \mathrm {a}[\mathrm {j}] \ \)を\( \ \mathrm {m} \ \)とします⇒\( \ \mathrm {a}[3]=5 \ \),\( \ \mathrm {a}[5]=6 \ \)
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=6 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=6>\mathrm {n}=5 \ \)なので\( \ \mathrm {YES} \ \)へ
⑨\( \ \mathrm {i} \ \)を\( \ \mathrm {i}+1 \ \)とします。⇒\( \ \mathrm {i}=4 \ \)
⑩\( \ \mathrm {i}>\mathrm {n}-1 \ \)かどうかを確認します。⇒\( \ \mathrm {i}=4=\mathrm {n}-1=4 \ \)なので\( \ \mathrm {NO} \ \)へ
④\( \ \mathrm {j} \ \)を\( \ \mathrm {i}+1 \ \)とします。⇒\( \ \mathrm {j}=5 \ \)
⑤\( \ \mathrm {a}[\mathrm {i}]>\mathrm {a}[\mathrm {j}] \ \)かどうかを確認します。⇒\( \ \mathrm {a}[4]=8>\mathrm {a}[5]=6 \ \)なので\( \ \mathrm {YES} \ \)へ
⑥\( \ \mathrm {m} \ \)を\( \ \mathrm {a}[\mathrm {i}] \ \)として\( \ \mathrm {a}[\mathrm {i}] \ \)を\( \ \mathrm {a}[\mathrm {j}] \ \)として\( \ \mathrm {a}[\mathrm {j}] \ \)を\( \ \mathrm {m} \ \)とします⇒\( \ \mathrm {a}[4]=6 \ \),\( \ \mathrm {a}[5]=8 \ \)
⑦\( \ \mathrm {j} \ \)を\( \ \mathrm {j}+1 \ \)とします。⇒\( \ \mathrm {j}=6 \ \)
⑧\( \ \mathrm {j}>\mathrm {n} \ \)かどうかを確認します。⇒\( \ \mathrm {j}=6>\mathrm {n}=5 \ \)なので\( \ \mathrm {YES} \ \)へ
⑨\( \ \mathrm {i} \ \)を\( \ \mathrm {i}+1 \ \)とします。⇒\( \ \mathrm {i}=5 \ \)
⑩\( \ \mathrm {i}>\mathrm {n}-1 \ \)かどうかを確認します。⇒\( \ \mathrm {i}=5>\mathrm {n}-1=4 \ \)なので\( \ \mathrm {YES} \ \)へ
⑪\( \ \mathrm {a}[1]~\mathrm {a}[\mathrm {n}] \ \)を「出力」します。⇒\( \ \mathrm {a}[1]=2 \ \),\( \ \mathrm {a}[2]=3 \ \),\( \ \mathrm {a}[3]=5 \ \),\( \ \mathrm {a}[4]=6 \ \),\( \ \mathrm {a}[5]=8 \ \)






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは