Contents
【問題】
【難易度】★★★☆☆(普通)
定格容量\( \ P \ \mathrm {[kV\cdot A ]} \ \),定格電圧\( \ V \ \mathrm {[V]} \ \)の星形結線の三相同期発電機がある。電機子電流が定格電流の\( \ 40 \ % \ \),負荷力率が遅れ\( \ 86.6 \ % \ \)( \(\cos 30°=0.866 \) ),定格電圧でこの発電機を運転している。このときのベクトル図を描いて,負荷角\( \ \delta \ \)の値\(\left[ ° \right] \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,この発電機の電機子巻線の\(1\)相当たりの同期リアクタンスは単位法で\( \ 0.915 \ \mathrm {p.u.} \ \),\(1\)相当たりの抵抗は無視できるものとし,同期リアクタンスは磁気飽和等に影響されず一定であるとする。
(1) \(0\) (2) \(15\) (3) \(30\) (4) \(45\) (5) \(60\)
【ワンポイント解説】
同期発電機の等価回路とベクトル図が描いて,三平方の定理を用いて解く問題で,ベクトル図の概念を理解する上で非常に良い問題と言えます。ぜひマスターするようにして下さい。本問の場合は計算をしなくてもベクトル図をできるだけ正確に描けば,答えが類推できますので,試験本番の間違い防止のためにベクトル図をできるだけきれいに描くと良いと思います。
1.同期発電機の等価回路とベクトル図
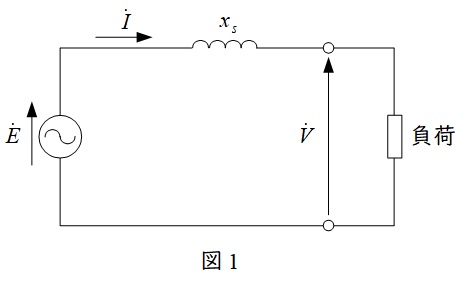
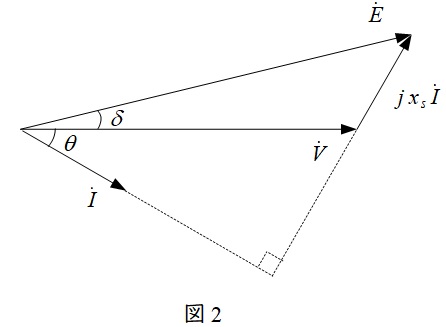
発電機の誘導起電力を\(\dot E\),負荷の端子電圧を\(\dot V\),同期リアクタンスを\(x_{\mathrm {s}}\),電機子電流を\(\dot I \)とすると,同期発電機の等価回路は図1のように描くことができ,そのベクトル図は図2のようになります。
【解答】
解答:(2)
題意に沿ってベクトル図を描くと図3のようになる。
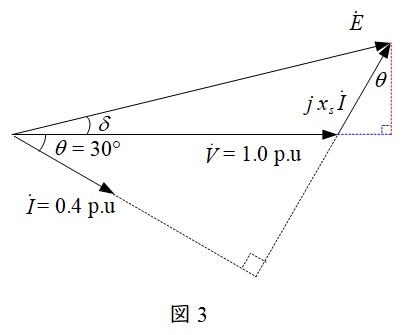
図3において,
\[
\begin{eqnarray}
x_{\mathrm {s}}I &=&0.915\times 0.4 \\[ 5pt ]
&=&0.366 \ \mathrm {[p.u. ]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,発電機の誘導起電力\(E\)は,
\[
\begin{eqnarray}
E &=&\sqrt {\left( V+x_{\mathrm {s}}I\sin \theta \right) ^{2}+\left( x_{\mathrm {s}}I\cos \theta \right) ^{2} } \\[ 5pt ]
&=&\sqrt {\left( 1+0.366 \times 0.5 \right) ^{2}+\left( 0.366 \times 0.866 \right) ^{2} } \\[ 5pt ]
&≒&1.2247 \ \mathrm {[p.u. ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,図3の赤点線の長さを求める関係において,
\[
\begin{eqnarray}
E\sin \delta &=&x_{\mathrm {s}}I\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
であるから,それぞれの値を代入すると,
\[
\begin{eqnarray}
1.2247\times \sin \delta &=&0.366 \times 0.866 \\[ 5pt ]
\sin \delta &=&0.25880 \\[ 5pt ]
\end{eqnarray}
\]
となり,\(\delta ≒15°\)と求められる。
※ \(\sin 15°≒0.2588\)ですが,この数値を暗記する必要はなく,\(\sin 0°=0\)と\(\sin 30°=0.5\)から,\(\delta \)がその間であると求めれば良いと思います。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは